Ivan Fesenko
| |||||||||||||||||||||||||
Read other articles:

Not to be confused with Bacar (disambiguation). For the villages in Iran, see Bakar, Iran (disambiguation). For the English singer, see Bakar (musician). Town in Primorje-Gorski Kotar County, CroatiaBakarTownGrad Bakar Town of Bakar FlagCoat of armsBakarLocation of Bakar in CroatiaCoordinates: 45°19′40″N 14°32′10″E / 45.32778°N 14.53611°E / 45.32778; 14.53611Country CroatiaCounty Primorje-Gorski Kotar CountySettled1st centuryNamed1288Free cityMay 13, 1...

Draw G's First BreathAlbum mini karya G.NADirilis14 Juli 2010Direkam2010GenreK-pop, pop, R&BDurasi17:24BahasaKoreaLabelCube Entertainment, Universal Music GroupKronologi G.NA Draw G's First Breath(2010) Black & White (2011)Black & White2011 Singel dalam album Draw G's First Breath Thing I'd Like to Do With My LoverDirilis: 5 Juli 2010 I'll Back Off So You Can Live BetterDirilis: 14 Juli 2010 Supa' SoloDirilis: Agustus 2010 Draw G's First Breath adalah album mini pertama pe...

Dachau Memorial Nandor Glid (12 December 1924 - 31 March 1997) was a Yugoslav sculptor, best known for designing the memorial sculpture at the Dachau concentration camp. Biography Glid was a Holocaust survivor who had been a forced laborer and partisan during the war and whose father and most of his family were murdered in Auschwitz.[1][2] From 1985 to 1989 he was Rector of the University of Arts in Belgrade.[3] After the war, he created a number of monuments memoriali...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Sola gratia – berita · surat kabar · buku · cendekiawan · JSTOR Lima solaReformasi Protestan Sola scriptura Sola fide Sola gratia Solus Christus Soli Deo glorialbsBagian dari seri tentangGereja LutheranM...

Igor LukšićIgor Lukšić Menteri KeuanganMasa jabatan16 Februari 2004 – 29 Desember 2010Perdana MenteriMilo ĐukanovićŽeljko ŠturanovićMilo Đukanović PendahuluMiroslav IvaniševićPenggantiincumbentPerdana Menteri MontenegroMasa jabatan29 Desember 2010 – 4 Desember 2012 Informasi pribadiLahir14 Juni 1976Bar, SR Montenegro, YugoslaviaPartai politikDemocratic Party of SocialistsAlma materUniversitas MontenegroPekerjaanEkonomSunting kotak info • L • B ...

У этого термина существуют и другие значения, см. Черни-Врых. Черни-Врыхболг. Черни връх Горы Витоша. Черни-Врых — на заднем плане. Высшая точка Абсолютная высота2290[1] м Относительная высота1259 м Расположение 42°33′49″ с. ш. 23°16′42″ в. д.HGЯO Страна Болг...

Pour la bande son adaptée, voir Le Mécano de la « General ». Le Mécano de la « General » Données clés Titre original The General Réalisation Buster KeatonClyde Bruckman Scénario Buster Keaton Clyde Bruckman Al BoasbergCharles Henry Smith Acteurs principaux Buster KeatonMarion Mack Sociétés de production Buster Keaton Comedies Pays de production États-Unis Genre Film burlesque Durée 94 minutes (R. de 2004) Sortie 1926 Pour plus de détails, voir Fiche techni...

Disambiguazione – Se stai cercando altri significati, vedi Bamberga (disambigua). BambergaCittà extracircondariale(DE) Bamberg Bamberga – Veduta LocalizzazioneStato Germania Land Baviera Distretto Alta Franconia CircondarioNon presente AmministrazioneSindacoAndreas Starke (SPD) TerritorioCoordinate49°53′30″N 10°53′30″E / 49.891667°N 10.891667°E49.891667; 10.891667 (Bamberga)Coordinate: 49°53′30″N 10°53′30″E / 49.89166...

Bbuddah... Hoga Terra BaapTheatrical release posterSutradaraPuri JagannadhProduserAbhishek BachchanPuri JagannadhViacom 18 Motion PicturesCeritaPuri JagannadhPemeranAmitabh BachchanHema MaliniSonu SoodPrakash RajSonal ChauhanRaveena TandonCharmy KaurAjaz KhanPenata musikSongs:Vishal-ShekharBackground Score:Anoop Rubens[1]SinematograferAmol RathodPenyuntingS R ShekharDistributorAmitabh Bachchan Corporation LimitedViacom 18 Motion PicturesTanggal rilis 1 Juli 2011 (2011-07-01...

State beach in Santa Cruz County, California, United States Twin Lakes State BeachShow map of CaliforniaShow map of the United StatesLocationSanta Cruz, CaliforniaNearest citySanta CruzCoordinates36°57′44″N 121°59′59″W / 36.96222°N 121.99972°W / 36.96222; -121.99972Governing bodyCalifornia Department of Parks and Recreation Twin Lakes State Beach is a beach located on Monterey Bay directly south of the Santa Cruz Yacht Harbor Santa Cruz, in coasta...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Census-designated place in Maine, United StatesMadawaska, MaineCensus-designated placeLocation of Madawaska, MaineCoordinates: 47°21′10″N 68°19′51″W / 47.35278°N 68.33083°W / 47.35278; -68.33083CountryUnited StatesStateMaineCountyAroostookTownMadawaskaArea[1] • Total5.39 sq mi (13.97 km2) • Land5.29 sq mi (13.70 km2) • Water0.10 sq mi (0.26 km2)Elevation574 ft (17...
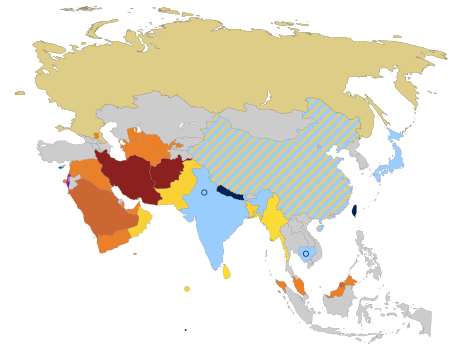
لا يتم عقد أو الاعتراف بزواج المثليين في نيبال. في عامي 2011 و 2012، حيث كانت الأمة تمر بمرحلة انتقالية، كانت هناك محاولة لإضافة لغة شاملة لمجتمع الميم إلى دستور صيغ حديثًا. ومع ذلك، فشلت المفاوضات بين الفصائل السياسية في ربيع عام 2012 وتم تعليق تنفيذ دستور مؤقت لحين إجراء انتخاب�...

Mountains in Germany North Palatine UplandsThe North Palatine Uplands around Münchweiler in Donnersbergkreis Highest pointPeakDonnersbergElevation686.5 m (2,252 ft)DimensionsLength70 km (43 mi)GeographyStateRhineland-Palatinate, SaarlandRange coordinates49°35′0″N 7°40′0″E / 49.58333°N 7.66667°E / 49.58333; 7.66667Parent rangeNorth French ScarplandsGeologyOrogenylow mountains Natural regions of the North Palatine Uplands (Nordpfälz...

Billiards games played on cloth-covered pocketless tables Not to be confused with the board game carrom. Carom billiardsA carom billiard table and billiard ballsHighest governing bodyUnion Mondiale de Billard (UMB)First played18th century FranceCharacteristicsContactNoTeam membersSingle opponents, doubles or teamsMixed-sexYes, sometimes in separate leagues/divisionsTypeIndoor, table, cue sportEquipmentBilliard ball, billiard table, cue stickVenueBilliard hall or home billiard roomPresenc...
Geography Now!Logo Geography Now! di YouTubeInformasi pribadiNegaraAmerika SerikatSitus webwww.geographynow.comInformasi YouTubeKanalGeography NowPembuatPaul BarbatoTahun aktif2014–sekarangGenrePendidikanPelanggan3,29 jutaTotal tayang438 juta Penghargaan Kreator 100.000 pelanggan 2016 1.000.000 pelanggan 2018 Diperbarui: 2 Januari 2023 Geography Now (juga digayakan sebagai Geography Now!) adalah saluran YouTube edukasi dari Amerika Serikat yang diciptakan dan dipandu oleh Paul Bar...

Royal Sovereign-class battleship For other ships with the same name, see HMS Repulse. A postcard of Repulse underway History United Kingdom NameRepulse Ordered1889 Naval Programme BuilderPembroke Dockyard Cost£915,302 Way numberNo. 1 Laid down1 January 1890 Launched27 February 1892 Completed21 April 1894 Commissioned25 April 1894 DecommissionedFebruary 1911 FateSold for scrap, 11 July 1911 General characteristics (as built) Class and typeRoyal Sovereign-class predreadnought battleship Displa...

Expressway in Guangdong and Macau, China This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: G0425 Guangzhou–Macau Expressway – news · newspapers · books · scholar · JSTOR (July 2022) Guangzhou–Macau Expressway广州-澳门高速公路Guang'ao Expressway广澳高速公路Guangzhou–Macau Exp...

観光 > 日本の観光 日本の観光(にほんのかんこう)では、日本国内の観光の変遷について記す。日本人による国外観光については海外旅行を参照。 概要 日本は大幅な観光収支赤字国だったが、世界経済フォーラムによる2017年の旅行・観光競争力ランキングで136カ国中4位(アジア1位)の観光大国に変貌した[1]。2019年の訪日外国人旅行者数は3188万人であっ�...

Hypothetical force carrier particle connected to dark matter Beyond the Standard ModelSimulated Large Hadron Collider CMS particle detector data depicting a Higgs boson produced by colliding protons decaying into hadron jets and electrons Standard Model Evidence Hierarchy problem Dark matter Dark energy Quintessence Phantom energy Dark radiation Dark photon Cosmological constant problem Strong CP problem Neutrino oscillation Theories Brans–Dicke theory Cosmic censorship hypothesis Fifth for...