Intersection theory
|
Read other articles:
تي معلومات شخصية تاريخ الميلاد القرن 14 ق.م الوفاة القرن 14 ق.م طيبة الزوج خپر خپرو رع آي الأولاد موت نجمت عائلة الأسرة المصرية الثامنة عشر الحياة العملية المهنة سياسية تعديل مصدري - تعديل لمعانٍ أخرى، طالع تي (توضيح). تي في الهيروغليفية...

Star Wars Episode VI:Return of the JediSutradaraRichard MarquandProduserHoward KazanjianGeorge LucasRick McCallum (SE)SkenarioGeorge LucasLawrence KasdanCeritaGeorge LucasPemeranMark HamillHarrison FordCarrie FisherBilly Dee WilliamsIan McDiarmidPenata musikJohn WilliamsSinematograferAlan HumePenyuntingSean BartonMarcia LucasDuwayne DunhamDistributor20th Century FoxTanggal rilis 25 Mei 1983 (1983-05-25) (USA) Durasi134 min. (original)135 min. (SE)BahasaBahasa InggrisAnggaran$32...

Palestinian footballer This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Shadi Shaban – news · newspapers · books · scholar · JSTOR (September 2017) (Learn how and when to remove this template mes...

Gouvernement Jules Dufaure (4) Troisième République Données clés président de la république Mac-Mahon Président du Conseil Jules Dufaure Formation 9 mars 1876 Fin 3 décembre 1876 Durée 8 mois et 24 jours Composition initiale Coalition Républicains Parti politique Union républicaine, Gauche républicaine, Centre gauche Représentation Ire législature 385 / 533 Gouvernement Jules Dufaure III Gouvernement Jules Simon modifier - modifier le code - voir Wikidata ...

ذي فيرف The verve الفرقة في إحدى الحفلات الموسيقية بداية 1990 الحياة الفنية النوع الروك البوب ألات مميزة الطبل: بيتر سالزبوري قيثارة البيس: سيمون جونز صوت وقيثارة: ريتشارد أشكروفت قيثارة: نيك مكابي قيثارة بلوحة المفاتيح: سيمون تونغ شركة الإنتاج إي إم آي أعمال مشتركة سونيت�...

Voce principale: Associazione Sportiva Lucchese Libertas 1905. Associazione Sportiva Lucchese LibertasStagione 1997-1998Sport calcio Squadra Lucchese Allenatore Luigi De Canio Presidente Egiziano Maestrelli Serie B15º posto Coppa ItaliaPrimo turno Maggiori presenzeCampionato: Colacone, Longo, Paci, Vannucchi (35) Miglior marcatoreCampionato: Paci (16) StadioPorta Elisa 1996-1997 1998-1999 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Associa...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hong Kong Airport Services – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to...

Dives-sur-Mer L'église Notre-Dame. Blason Administration Pays France Région Normandie Département Calvados Arrondissement Lisieux Intercommunalité CC Normandie-Cabourg-Pays d'Auge(siège) Maire Mandat Pierre Mouraret 2020-2026 Code postal 14160 Code commune 14225 Démographie Gentilé Divais Populationmunicipale 5 174 hab. (2021 ) Densité 801 hab./km2 Population agglomération 36 814 hab. (2016) Géographie Coordonnées 49° 17′ 08″ nord, 0°&...

Questa voce o sezione sull'argomento stadi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Rogers CentreSkyDome Informazioni generaliStato Canada Ubicazione1 Blue Jays WayToronto, Ontario M5V 1J3 Inizio lavori3 ottobre 1986 Inaugurazione3 giugno 1989 Costo570 000 000 C$ ProprietarioRogers C...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Serge Chiesa Nazionalità Francia Altezza 168 cm Calcio Ruolo Centrocampista Termine carriera 1989 CarrieraGiovanili 1960-1969 MontferrandSquadre di club1 1969-1983 Olympique Lione475 (120)1983-1985 Orléans64 (11)1985-1989 Clermont Foot92 (11)Nazionale 1969-1974 Francia12 (3) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Statistiche aggiornate al 13 aprile 2012 Modifica da...

Rotherham United 2015–16 football seasonRotherham United2015–16 seasonChairmanTony StewartManagerSteve Evans (left on 28 September 2015)Eric Black (caretaker manager 28 September 2015 – 9 October 2015)Neil Redfearn (9 October 2015 – 8 February 2016)Neil Warnock (11 February 2016 – 18 May 2016)StadiumAESSEAL New York StadiumChampionship21stFA CupThird Round Proper(knocked out by Leeds United)League CupSecond Round(knocked out by Norwich City)Top goalscorerLeague: Derbyshire (8)All: ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Terdapat beberapa tafsir dari rujukan Alkitab untuk Elia sebagai orang Tisbe. Orang Tisbe adalah sebuah demonim yang disematkan kepada Nabi Elia dalam Perjanjian Lama (1 Raja–Raja 17:1, 1 Raja–Raja 21:17–28, 2 Raja–Raja 1:3–8 dan 2 Raja–Raj...

福海寺 雲會堂所在地 兵庫県神戸市兵庫区西柳原町10-10位置 北緯34度40分11.99秒 東経135度10分5.03秒 / 北緯34.6699972度 東経135.1680639度 / 34.6699972; 135.1680639座標: 北緯34度40分11.99秒 東経135度10分5.03秒 / 北緯34.6699972度 東経135.1680639度 / 34.6699972; 135.1680639山号 大光山宗派 臨済宗南禅寺派寺格 諸山本尊 釈迦如来(奈良時代作・木心乾漆造)創建年 ...

Voce principale: Aurora Pro Patria 1919. Pro Patria et Libertate Unione degli Sports BustesiStagione 1940-1941Sport calcio Squadra Pro Patria Allenatore Antonio Bernacchi e Natale Masera Presidente Giovanni Calcaterra Serie C1º posto nel girone C, 2º nel girone finale A. Promossa in Serie B. Maggiori presenzeCampionato: Gallazzi (36) Miglior marcatoreCampionato: Gallazzi (19) 1939-1940 1941-1942 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l...
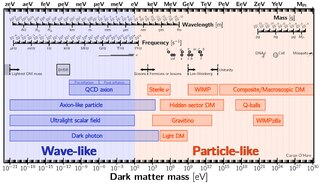
Concept in cosmology For other uses, see Dark Matter (disambiguation). Not to be confused with antimatter or dark energy. Unsolved problem in physics: What is dark matter? How was it generated? (more unsolved problems in physics) Part of a series onPhysical cosmology Big Bang · Universe Age of the universe Chronology of the universe Early universe Inflation · Nucleosynthesis Backgrounds Gravitational wave (GWB) Microwave (CMB) · Neutrino (CNB) Expansion · Future Hubble...

Railway station serving the village of Cookham, Berkshire, England CookhamLooking south towards Furze PlattGeneral informationLocationCookham, Windsor and MaidenheadEnglandGrid referenceSU886850Managed byGreat Western RailwayPlatforms1Other informationStation codeCOOClassificationDfT category EHistoryOpened1 August 1854Original companyWycombe RailwayPre-groupingGreat Western RailwayPost-groupingGreat Western RailwayPassengers2018/19 0.227 million2019/20 0.221 million2020/21 41,1802021/22 0.11...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Sibley Railroad Bridge – news · newspapers · books · scholar · JSTOR (August 2021) This article i...

American social activist (1940–2015) Julian BondBond in 2000Chair of the National Association for the Advancement of Colored PeopleIn office1998–2010Preceded byMyrlie Evers-WilliamsSucceeded byRoslyn BrockMember of the Georgia State Senatefrom the 39th districtIn officeJanuary 13, 1975 – January 12, 1987Preceded byHorace WardSucceeded byHildred ShumakeMember of the Georgia House of RepresentativesIn officeJanuary 9, 1967 – January 13, 1975Succeeded byMildred GloverCo...

![{\displaystyle \lambda _{M}(a,b)=\langle a\smile b,[M]\rangle \in \mathbf {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5224441f15083b73af07a158d2c8f3ddc7e2ce70)






