Great ditrigonal icosidodecahedron
Type	Uniform star polyhedron
Elements	F = 32, E = 60 V = 20 (χ = −8)
Faces by sides	20{3}+12{5}
Coxeter diagram
Wythoff symbol	3/2 | 3 5 3 | 3/2 5 3 | 3 5/4 3/2 | 3/2 5/4
Symmetry group	Ih, [5,3], *532
Index references	U47, C61, W87
Dual polyhedron	Great triambic icosahedron
Vertex figure	((3.5)3)/2
Bowers acronym	Gidtid

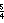
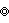
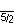
In geometry, the great ditrigonal icosidodecahedron (or great ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U₄₇. It has 32 faces (20 triangles and 12 pentagons), 60 edges, and 20 vertices.^[1] It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 | 3 5⁄4 gives Coxeter diagram = . It has extended Schläfli symbol a{5⁄2,3} or c{3,5⁄2}, as an altered great stellated dodecahedron or converted great icosahedron.

Its circumradius is ${\textstyle {\frac {\sqrt {3}}{2}}}$ times the length of its edge,^[2] a value it shares with the cube.

Its convex hull is a regular dodecahedron. It additionally shares its edge arrangement with the small ditrigonal icosidodecahedron (having the triangular faces in common), the ditrigonal dodecadodecahedron (having the pentagonal faces in common), and the regular compound of five cubes.

a{5,3}	a{5/2,3}	b{5,5/2}
=	=
Small ditrigonal icosidodecahedron	Great ditrigonal icosidodecahedron	Ditrigonal dodecadodecahedron
Dodecahedron (convex hull)	Compound of five cubes

• VRML model: [1]
• MathWorld

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.

• v
• t
• e