Global field
|
Read other articles:
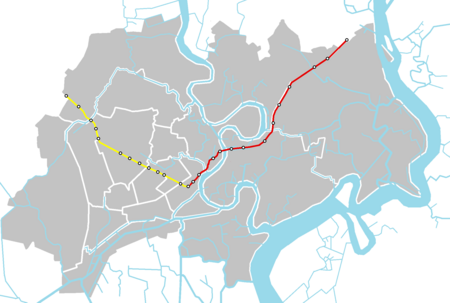
Ho Chi Minh City MetroInfoPemilikOtoritas Manajemen Perkeretaapian KotaWilayahHo Chi Minh City, VietnamJenisAngkutan cepatJumlah jalur1 (sedang dibangun) 7 (direncanakan)Jumlah stasiun14 (sedang dibangun)OperasiAkan dimulai2024[1]Waktu antara2 menit[2]TeknisPanjang sistem197 km (122,4 mi) (Line 1)Lebar sepur1.435 mm (4 ft 8+1⁄2 in) sepur standar[2]ListrikListrik aliran atasKecepatan tertinggi80 km/h (50 mph)[2] Peta...

2001 video gameThe King of Fighters 2001Developer(s)Eolith[a]Playmore (DC, PS2)Publisher(s) SNK Sun Amusement (AES)Playmore (DC)PlayStation 2JP: SNK PlaymoreKOR: MEGA SNK Playmore (WIN)HAMSTER Corporation (PS4/Switch/Xbox One) Director(s)Lee Sen HoProducer(s)Chil Suk ChoiDesigner(s)H. IgaProgrammer(s)S. FujinukiArtist(s)Hiroaki HashimotoNonaWriter(s)TeampowComposer(s)Kikuko HatayaMasahiko HatayaSeriesThe King of FightersPlatform(s) Arcade Dreamcast, Microsoft Windows, Neo Geo AES, Nin...

Station météorologiqueEnsemble d'instruments d'une station météo conventionnelle.Type Station d'observation (d)CaractéristiquesComposé de Instrument de mesure météorologiqueUtilisationUsage Observation météorologique de surfacemodifier - modifier le code - modifier Wikidata Une station météorologique, parfois désignée par synecdoque abri météorologique, est un ensemble de capteurs qui enregistrent et fournissent des mesures physiques et des paramètres météorologiques liés ...

Student-run radio station at Iowa State University in Ames, Iowa For other uses, see Kure (disambiguation). 88.5 KUREAmes, IowaBroadcast areaAmes, IowaFrequency88.5 MHzBrandingIowa State's Student-Run Radio StationProgrammingFormatCollege RadioOwnershipOwnerResidence Association Broadcasting Services, Inc.HistoryFormer call signsKMRA (1949–1950) KMRI (1950–1961) KISU (1961–1970) KPGY (1970–1983) KUSR (1983–1996)Technical informationFacility ID55777ClassAERP630 wattsHAAT22.0 metersTr...

Essam El-Hadary Mesir dengan Salah kalah dari Arab Saudi, 2018Informasi pribadiNama lengkap Essam El-HadaryTanggal lahir 15 Januari 1973 (umur 51)Tempat lahir Damietta, MesirTinggi 190 cm (6 ft 3 in)Posisi bermain Penjaga gawangInformasi klubKlub saat ini IsmailyKarier senior*Tahun Tim Tampil (Gol)2018 – Ismaily 0 (0)Tim nasional1996 – Mesir 159 (0) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Essam El-Hadary (lahir 15 Januari 1973) adalah seo...

Town in Texas, United StatesTown of PantegoTownLocation of Pantego in Tarrant County, TexasCoordinates: 32°42′55″N 97°09′17″W / 32.71528°N 97.15472°W / 32.71528; -97.15472CountryUnited StatesStateTexasCountyTarrantIncorporated (city)May 22, 1952Government • MayorDoug Davis 2017-Present Melody Paradise 2010-2017[1]Area[2] • Total1.04 sq mi (2.70 km2) • Land1.04 sq mi (2.70 km2...

For other uses, see Naqada (disambiguation). Last phase of the Naqada culture of ancient Egyptian prehistory Naqada IIINaqadaNaqada III (Egypt)Show map of EgyptNaqadaNaqada III (Northeast Africa)Show map of Northeast AfricaGeographical rangeEgyptPeriodEarly Bronze IDatesc. 3,300 BC – 2,900 BC[1]Major sitesNaqada, Tarkhan, NekhenPreceded byNaqada IIFollowed byEarly Dynastic Period (Egypt) The Narmer Palette, thought to mark the unification of Upper and Lower Egypt; note the ima...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

An ecological island is a term used in New Zealand, and increasingly in Australia, to refer to an area of land (not necessarily an actual island) isolated by natural or artificial means from the surrounding land,[1] where a natural micro-habitat exists amidst a larger differing ecosystem. In New Zealand the term is used to refer to one of several types of nationally protected areas. In artificial ecological islands (also known as mainland islands): all non-native species (at least pre...

Part of a series onSex and sexuality inspeculative fiction Main topics Sex and sexuality Gender Women Reproduction Genres Women in comics Feminist science fiction Slash fiction LGBT themes In comics (characters) In mythology In horror fiction Lesbian vampires Yaoi Yuri Recurring elements Sex in space Male pregnancy Single-gender worlds Lesbian vampires Woman warriors Gynoids Awards and conventions Gaylactic Network Gaylaxicon Gaylactic Spectrum Awards Lambda Literary Awards Otherwise Aw...

Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (December 2022) (Learn how and when to remove this message) Men's 400 metres at the 2016 European Athletics ChampionshipsVenueOlympic StadiumLocationAmsterdamDates6 July (heats)7 July (semifinals)8 July (final)Competitors32 from 17 nationsWinning time45.29Medalists Martyn Ro...

فيفي عبده فيفي عبده 2018 معلومات شخصية اسم الولادة عطيات عبد الفتاح إبراهيم[1] الميلاد 26 أبريل 1953 (71 سنة) ميت أبو الكوم مواطنة مصر الأولاد عزة مجاهد الحياة العملية المهنة راقصة، وممثلة اللغة الأم العربية اللغات العربية سنوات النشاط...

Worship of an idol as though it were a god Idol worship redirects here. For the American hip hop group, see Idle Warship. False idols redirects here. For the Tricky album, see False Idols. For the Veil of Maya album, see False Idol (album). Moses Indignant at the Golden Calf, painting by William Blake, 1799–1800 Idolatry is the worship of a cult image or idol as though it were a deity.[1][2][3] In Abrahamic religions (namely Judaism, Samaritanism, Christianity, the B...

United States Army Medal of Honor recipient (born 1944) Harold A. FritzNickname(s)HalBorn (1944-02-21) February 21, 1944 (age 80)Chicago, Illinois, U.S.AllegianceUnited StatesService/branchUnited States ArmyYears of service1966–1993RankLieutenant ColonelUnit11th Armored Cavalry RegimentBattles/warsVietnam WarAwardsMedal of HonorSilver StarLegion of MeritBronze Star Medal (2)Purple Heart (2) Harold Arthur Hal Fritz (born February 21, 1944) is a retired United States Army officer an...

Aggressive and fast subgenre of punk rock Hardcore punkMinor Threat performing in 1981Other namesHardcoreStylistic originsPunk rockproto-punk[1]Cultural originsLate 1970s to early 1980s, Southern California,[2][3][4][5][6][7] Vancouver, Knoxville,[8] San Francisco,[7][1] Washington, D.C. area[7]Derivative formsAlternative rockblack metal[9][10]crustcore[11]death metalemogrungenoise ...

The following is a list of events predicted and scheduled to take place in the year 2024 in Ethiopia. List of events ← 2023 2022 2021 2024 in Ethiopia → 2025 2026 2027 Decades: 2000s 2010s 2020s See also:Other events of 2024Timeline of Ethiopian history Incumbents President: Sahle-Work Zewde Prime Minister: Abiy Ahmed Events Ongoing War in Amhara[1][verification needed][2][3][4][5][verification needed] OLA insurgency Gambela ...
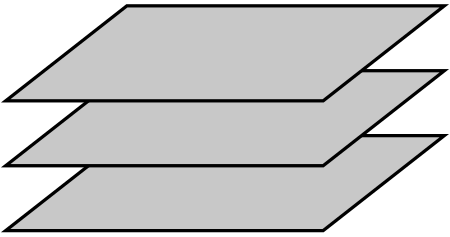
Dois planos não paralelos no espaço Na matemática, um plano é um ente primitivo geométrico infinito a duas dimensões. Nos Elementos de Euclides, não possui definição enquanto conceito genérico. Mas um plano qualquer é definido, ou determinado, de várias formas equivalentes. Em uma geometria Infinitesimal, é possível definir de forma genérica um plano como um conjunto infinito de retas, onde todas são perpendiculares a um mesmo vetor (vetor normal do plano). Planos no espaço U...

Realm of the Elves in Tolkien's legendarium For the video game developer, see MC Lothlorien. LothlórienJ. R. R. Tolkien's legendarium locationIn-universe informationOther name(s)LórienLórinandLaurelindórenanthe Golden Woodthe Hidden Land[1]DwimordeneTyperealm of the ElvesRulerAmdír, Amroth (Second Age), Celeborn and Galadriel (Second and Third Ages)LocationsCaras Galadhon, Cerin Amroth, Naith or Angle, the river Nimrodel, the river SilverlodeGeographywestern WilderlandLifespanFou...

Branch of phylogeny that analyzes genetic, hereditary molecular differences Molecular phylogenetics (/məˈlɛkjʊlər ˌfaɪloʊdʒəˈnɛtɪks, mɒ-, moʊ-/[1][2]) is the branch of phylogeny that analyzes genetic, hereditary molecular differences, predominantly in DNA sequences, to gain information on an organism's evolutionary relationships. From these analyses, it is possible to determine the processes by which diversity among species has been achieved. The result of a mol...

Ini adalah sebuah nama Indonesia yang tidak menggunakan nama keluarga. Nama Mukti adalah sebuah patronimik, dan tokoh ini dipanggil dengan nama depannya, Lena Maryana. Lena Maryana Duta Besar Indonesia untuk Kuwait ke-13PetahanaMulai menjabat 25 Oktober 2021PresidenJoko WidodoPendahuluTri TharyatPenggantiPetahanaAnggota Dewan Perwakilan Rakyat Republik IndonesiaMasa jabatan2 Oktober 2018 – 30 September 2019PendahuluOkky AsokawatiPenggantiTidak ada[a]Daerah pemilihan...




