Gerhard Behrendt
|
Read other articles:

For the neighbourhood in Düsseldorf, see Düsseldorf-Niederkassel. Town in North Rhine-Westphalia, GermanyNiederkassel Town Coat of armsLocation of Niederkassel within Rhein-Sieg-Kreis district Niederkassel Show map of GermanyNiederkassel Show map of North Rhine-WestphaliaCoordinates: 50°49′N 7°02′E / 50.817°N 7.033°E / 50.817; 7.033CountryGermanyStateNorth Rhine-WestphaliaAdmin. regionKöln DistrictRhein-Sieg-Kreis Subdivisions7Government • Mayor ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2017. Koki HabataInformasi pribadiNama lengkap Koki HabataTanggal lahir 22 Juli 1983 (umur 40)Tempat lahir Prefektur Wakayama, JepangPosisi bermain PenyerangKarier senior*Tahun Tim Tampil (Gol)2002-2003 Gamba Osaka 2004 Sagan Tosu * Penampilan dan gol di ...

Peta lokasi San Felipe San Felipe adalah munisipalitas yang terletak di provinsi Zambales, Filipina. Menurut sensus tahun 2000, wilayah ini memiliki jumlah penduduk sebesar 21.322 jiwa dan 4.094 rumah tangga. Barangay San Felipe terbagi menjadi 11 barangay. Amagna (Pob.) Apostol (Pob.) Balincaguing Farañal (Pob.) Feria (Pob.) Maloma Manglicmot (Pob.) Rosete (Pob.) San Rafael Santo Niño Sindol Pranala luar Philippine Standard Geographic Code Diarsipkan 2012-04-13 di Wayback Machine. 2000 Phi...

Untuk pengertian lain silakan lihat Kurowo Kurowo (Desa)Negara PolandiaProvinsiPodlasiePowiatWysokie MazowieckieGminaKobylin-Borzymy (desa gmina)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Postal code18-204Car platesBWM Gmina Kobylin-Borzymy Kurowo adalah desa di kecamatan Kobylin-Borzymy, powiat Wysokie Mazowieckie, provinsi Podlasie, Polandia. Gallery Desa Kurowo Kurowo seat Taman Nasional Narew Logo Taman Nasional Narew Taman Nasional Narew Pranala luar Koordinat:...

بيتر لاكس معلومات شخصية الميلاد 1 مايو 1926 (98 سنة)[1][2][3] بودابست مواطنة المجر الولايات المتحدة عضو في الأكاديمية الفرنسية للعلوم، والأكاديمية النرويجية للعلوم والآداب، والأكاديمية الوطنية للعلوم، وأكاديمية العلوم في الاتحاد السوفيتي[...

The Young and the RestlessGenreOpera sabunPembuatWilliam J. BellLee Philip BellDitulis olehShelly AltmanJean PassananteTracey ThomsonSutradaraSee belowPemeranCast membersNegara asal Amerika SerikatBahasa asliInggrisJmlh. musim50Jmlh. episode12625 (pada 25 Mei 2023) ([episode])ProduksiProduser eksekutifJill Farren Phelps (2012–sekarang)(and others)ProduserSee belowDurasi30 menit per episode (1973–80)60 menit per episode (1980–sekarang)Rumah produksiBell Dramatic Serial CompanyCorda...

Football matchCopa del Generalísimo 1939 FinalSevilla FC, championsEvent1939 Copa del Generalísimo Sevilla Racing de Ferrol 6 2 Date25 June 1939VenueMontjuïc, BarcelonaRefereeJesús ArribasAttendance60,000 [1]← 1936 1940 → Main article: 1939 Copa del Generalísimo The Copa del Generalísimo 1939 Final was the 37th final of the King's Cup. The final was played at Montjuïc in Barcelona, on 25 June 1939, being won by Sevilla FC, who beat Racing Club de Ferrol 6-2. Match d...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

ديدهام الإحداثيات 41°54′31″N 94°49′22″W / 41.908611111111°N 94.822777777778°W / 41.908611111111; -94.822777777778 [1] تاريخ التأسيس 1883 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة كارول خصائص جغرافية المساحة 1.499716 كيلومتر مربع1.499717 كيلومتر مربع (1 أبر...

Untuk orang lain dengan nama yang sama, lihat George Carey. Yang Mulia dan Right HonourableThe Lord Carey of CliftonPCmantan Uskup Agung CanterburyGerejaGereja InggrisProvinsi gerejawiProvinsi CanterburyKeuskupanKeuskupan Canterburydidelegasikan menjadi Uskup DoverMasa jabatan1991–2002PendahuluRobert RunciePenerusRowan WilliamsJabatan lainUskup asisten kehormatan di Swansea & Brecon (2004–?), dalam Southwark dan di Bristol; di Oxford (?–2017)Life peer (2002);Uskup Bath dan Well...

شيكاغو فاير الاسم الكامل نادي حريق شيكاغو لكرة القدمChicago Fire Football Club اللقب الماكينة الحمراء - The Red Machine الحريق - The Fire الاسم المختصر شيكاغو فاير تأسس عام 1997 (منذ 27 سنة) الملعب تويوتا بارك(السعة: 20,000) البلد الولايات المتحدة الدوري دوري النخبة الأمريكي الإدارة الرئيس أندرو ها�...
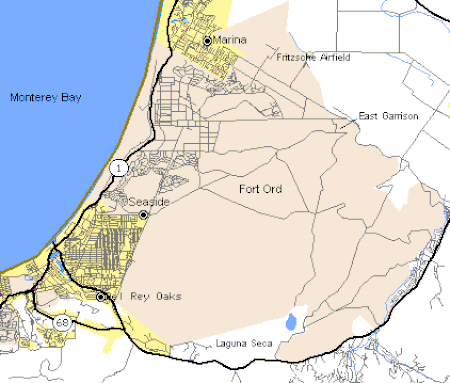
Former U.S. Army Fort in California This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fort Ord – news · newspapers · books · scholar · JSTOR (December 2014) (Learn how and when to remove this message) Fort Ord National MonumentMonterey Bay area, California Abandoned Army barracks at Fort OrdFort Ord National M...

Історія Європейського Союзу до 19451945-19571958–19721973-19931993-2004з 2004Портал «Європейський Союз» переглянутиобговоритиредагувати Період спільності європейських країн у післявоєнні роки (1945–1957) вважається початком та першим кроком до їх єднання. У 1951 році було створено перше екон...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2020) المقالة الرئيسة: بطولة آسيا للشباب تحت 19 عاما 2016 هذه قائمة بتشكيلات بطولة آسيا للشباب تحت 19 عاما 2016 التي أ...

Dobrich TV Tower is a 190-metre high TV tower built of reinforced concrete near Dobrich in Bulgaria. Dobrich TV Tower, which was designed by Petar Andreev, was completed in 1979 and has an observation deck open for tourists. The tower is located in the southern edge of the city, in between the Gaazi Baba and Prostor neighbourhoods, just northeast of Temple Arhangel Mihail and the cemetery connected to it. Dobrich Tv tower Dobrich AM transmitter A few kilometres away from Dobrich TV Tower, the...

British actress (1893–1977) For the American artist, see Margaret Ann Withers. Margaret Withers 1939 Spotlight photo Margaret Withers (6 July 1893 – 26 October 1977) was a British actress mainly on the stage.[1][2][3] Filmography Year Title Role Notes 1935 Car of Dreams Mrs. Hart 1943 The Demi-Paradise Mrs. Elliston Uncredited 1944 Don't Take It to Heart Mrs. Smith 1945 Great Day Miss Jane Tyndale 1945 The Seventh Veil Uncredited 1947 Dual Alibi Blackpool Landlady ...

For other places with the same name, see Písek (disambiguation). Town in South Bohemian, Czech RepublicPísekTownChurch of the Nativity of the Virgin Mary, town walls and the Otava FlagCoat of armsPísekLocation in the Czech RepublicCoordinates: 49°18′32″N 14°8′51″E / 49.30889°N 14.14750°E / 49.30889; 14.14750Country Czech RepublicRegionSouth BohemianDistrictPísekFounded1254Government • MayorMichal ČapekArea • Total63.23 ...

Cambodian politician and war criminal (born 1931) In this Cambodian name, the surname is Khieu. In accordance with Cambodian custom, this person should be referred to by the given name, Samphan. Khieu Samphanខៀវ សំផនSamphan in 2014Chairman of the State PresidiumIn office11 April 1976 – 7 January 1979Prime MinisterPol PotDeputySo PhimNhim Ros[1]LeaderPol Pot (General Secretary)Preceded byNorodom Sihanoukas President of the State PresidiumSucceeded byHeng Samrin...

Jörg BöhmeBöhme ai tempi dello Schalke 04Nazionalità Germania Altezza174 cm Calcio RuoloAllenatore (ex centrocampista) Squadra Schalke 04 II Termine carriera2008 - calciatore CarrieraGiovanili 1982-1986BSG Chemie Zeitz1986-1992 Carl Zeiss Jena Squadre di club1 1992-1994 Carl Zeiss Jena22 (2)1994-1995 Norimberga16 (1)1995-1996 Eintracht Francoforte18 (1)1996-1998 Monaco 186023 (1)1998-2000 Arminia Bielefeld50 (3)2000-2004 Schalke 04101 (23)2005-...

Mathematical function whose derivative exists A differentiable function In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp...

