Gallai–Hasse–Roy–Vitaver theorem
|
Read other articles:

Pengeboman atom Hiroshima dan NagasakiBagian dari Perang Pasifik, Perang Dunia IIAwan jamur bom atom di langit Hiroshima (kiri) dan Nagasaki (kanan).Tanggal6 Agustus dan 9 Agustus 1945LokasiHiroshima dan Nagasaki, JepangHasil Sekutu menangPihak terlibat Amerika Serikat Britania Raya JepangTokoh dan pemimpin William S. Parsons Paul Tibbets Robert A. Lewis[1] Charles Sweeney Frederick Ashworth Shunroku HataPasukan Manhattan District: 50 A.S., 2 Britania50...

Bagian dari seriGereja Katolik menurut negara Afrika Afrika Selatan Afrika Tengah Aljazair Angola Benin Botswana Burkina Faso Burundi Chad Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Guinea Khatulistiwa Jibuti Kamerun Kenya Komoro Lesotho Liberia Libya Madagaskar Malawi Mali Maroko Mauritania Mauritius Mesir Mozambik Namibia Niger Nigeria Pantai Gading Republik Demokratik Kongo Republik Kongo Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland ...

Lupin the 3rd vs Detective ConanSampul DVDPemeranLihat Pengisi suaraDistributorVapTanggal rilis27 Maret 2009Negara JepangBahasaBahasa Jepang Lupin the 3rd vs Detective Conan (ルパン三世VS名探偵コナンcode: ja is deprecated , Rupan Sansei vs Meitantei Konan) adalah spesial TV dari seri Lupin III dan Detektif Conan. Spesial TV ini ditayangkan pada 27 Maret 2009. Pengisi suara Arsène Lupin III - Kanichi Kurita Daisuke Jigen - Kiyoshi Kobayashi Goemon Ishikawa XIII - Makio Inoue F...

1963 murder of the 35th U.S. President Kennedy assassination redirects here. For the assassination of John's brother Robert, see Assassination of Robert F. Kennedy. November 22, 1963 redirects here. For the date, see November 22, 1963 (Friday). Assassination of John F. KennedyPresident John F. Kennedy, his wife Jacqueline, Texas governor John Connally, and Connally's wife Nellie in the presidential limousine minutes before the assassination in DallasLocationDealey Plaza in Dallas, Texas, U.S....

Vadi AkbarLahirVadie Akbar Kalamata8 Agustus 1995 (umur 28)Jakarta, IndonesiaKebangsaanIndonesiaAlmamaterUniversitas IndonesiaPekerjaanPenyanyiCEOTahun aktif2014–sekarangTempat kerjaV8 SoundKeluarga Vidi Aldiano (kakak) Sheila Dara Aisha (kakak ipar) Karier musikGenreJazzswingpop jazzInstrumenVokalLabelVAArtis terkaitChaseiro All Stars Vadie Akbar Kalamata (lahir 8 Agustus 1995) adalah penyanyi berkebangsaan Indonesia. Vadi memulai debut di industri musik pada tahun 2014 dengan m...

Private, non-profit school in Batu Feringghi, Penang, Penang Island, MalaysiaThe International School of Penang (Uplands)Respect for Self; Respect for OthersLocationBatu Feringghi, Penang, Penang IslandMalaysiaCoordinates5°28′12″N 100°14′59″E / 5.470053°N 100.249676°E / 5.470053; 100.249676InformationTypePrivate, non-profitMottoRespect for Self; Respect for OthersFounded1955[citation needed]PrincipalMarc MesichGenderMixedAge range4–19Enrollment±...

Hospital in New York, United StatesStony Brook University HospitalStony Brook MedicineEntrance to Stony Brook University HospitalGeographyLocation101 Nicolls Road, Stony Brook, New York, United StatesOrganizationTypeTeachingAffiliated universityRenaissance School of Medicine at Stony Brook UniversityServicesEmergency departmentLevel I trauma centerBeds695HelipadFAA LID: 13NYHistoryFormer name(s)Stony Brook University Medical CenterOpened1980LinksWebsitewww.stonybrookmedicine.eduListsHospitals...
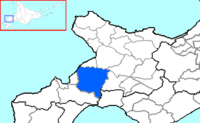
Distrik Isoya di Subprefektur Shiribeshi. Isoya (磯谷郡code: ja is deprecated , Isoya-gun) adalah sebuah distrik yang yang berada di wilayah Subprefektur Shiribeshi, Hokkaido, Jepang. Per 31 Januari 2024, distrik ini memiliki estimasi jumlah penduduk sebesar 4.500 jiwa dan kepadatan penduduk sebesar 10 orang per km2. Distrik ini memiliki luas wilayah sebesar 449,78 km2. Kota kecil dan desa Rankoshi lbs HokkaidoSapporo (Ibu kota prefektur)lbsSubprefektur IshikariSapporoDistrik kota Ats...

Former electorate in Auckland, New Zealand Eden electorate boundaries between 1993 and 1996 Eden, a former New Zealand parliamentary electorate, lay in the general area of the suburb of Mount Eden in the city of Auckland. Population centres The 1870 electoral redistribution was undertaken by a parliamentary select committee based on population data from the 1867 census. Eight sub-committees were formed, with two members each making decisions for their own province; thus members set their own ...

American media company Not to be confused with other organizations named Scripps. The E. W. Scripps CompanyScripps headquarters in Cincinnati, OhioCompany typePublicTraded asNasdaq: SSP (Class A) (1988–1991; 2018–present)NYSE: SSP (1991–2018)IndustryBroadcast televisionFoundedNovember 2, 1878; 145 years ago (November 2, 1878) (as the Penny Press) in Cleveland, OhioFounderEdward W. ScrippsHeadquartersScripps Center, Cincinnati, Ohio, U.S.Key peopleKim Williams...

Voce principale: Rende Calcio 1968. Società Sportiva RendeStagione 1986-1987Sport calcio Squadra Rende Allenatore Gesualdo Albanese Presidente Raffaele Mazzuca Serie C216º nel girone D. Retrocede nel Campionato Interregionale. Maggiori presenzeCampionato: Massarini, Sarpa (32) Miglior marcatoreCampionato: Vitelli (11) 1985-1986 1987-1988 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti la Rende Calcio 1968 nelle competizioni ufficiali della stag...

Questa voce sull'argomento attori statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Jamie Farr Jamie Farr, pseudonimo di Jameel Joseph Farah (Toledo, 1 luglio 1934), è un attore statunitense noto per l'interpretazione del caporale Klinger nella serie M*A*S*H[1][2]. Indice 1 Biografia 2 Filmografia parziale 2.1 Cinema 2.2 Televisione 3 Doppiatori italiani 4 Note 5 Collegament...

رسم مبياني لبيانات عشوائية تحقق أخطاء نمذجتها وفق الانحدار الخطي تجانس التباين تساوي التباين أو تجانس التباين (بالإنجليزية: Homoscedasticity) هو خاصية متتالية أو متجهة متغيرات عشوائية، يكون فيها لكل المتغيرات العشوائية نفس التباين.[1] الخاصية المعاكسة هي اختلاف التباين (بال...

Part of a series on theCarbon cycle By regions Terrestrial Marine Atmospheric Deep carbon Soil Permafrost Boreal forest Geochemistry Carbon dioxide In the atmosphere Ocean acidification Removal Satellite measurements Forms of carbon Total carbon (TC) Total organic carbon (TOC) Total inorganic carbon (TIC) Dissolved organic carbon (DOC) Dissolved inorganic carbon (DIC) Particulate organic carbon (POC) Particulate inorganic carbon (PIC) Primary production marine Black carbon Blue carbon Kerogen...

Pour les articles homonymes, voir Shirayuki. ShirayukiPhotographie de l'empereur Hirohito à cheval sur Shirayuki, dans les années 1930.BiographieNaissance 1921Haras de BábolnaDécès 25 octobre 1947Shimōsa Imperial Stock Farm (d)Propriétaire Hirohitomodifier - modifier le code - modifier Wikidata Shirayuki (白雪?), ou Shira-Yuki, ou encore Sirayuki (en japonais, « Neige blanche »), est un cheval que montait l'empereur du Japon Hirohito au début de l'ère Shōwa. Ce cheval...

Congressional committee United States House Permanent Select Committee on IntelligencePermanent select committeeActiveUnited States House of Representatives118th CongressSeal of the House Permanent Select Committee on IntelligenceHistoryFormedJuly 14, 1977Formerly known asSelect Committee on IntelligenceLeadershipChairMike Turner (R) Since January 9, 2023Ranking memberJim Himes (D) Since February 1, 2023StructureSeats25Political partiesMajority (14) Republican (14) Minority (11) ...
Women's 100 metres at the 2023 World ChampionshipsVenueNational Athletics CentreDates20 August (heats)21 August (semi-final & final)Competitors56 from 38 nationsWinning time10.65 CRMedalists Sha'Carri Richardson United States Shericka Jackson Jamaica Shelly-Ann Fraser-Pryce Jamaica← 20222025 → Video on YouTubeOfficial Video Events at the2023 World ChampionshipsTrack events100 mmenwomen200 m...

Geoffrey MarcyLahir29 September 1954 (umur 69)KebangsaanAmerikaAlmamaterUniversitas California, Los Angeles (B.A.)Universitas California, Santa Cruz (Ph.D.)Dikenal ataspenemuan eksoplanetPenghargaanMedali Henry Draper (2001)Penghargaan Shaw (2005)Karier ilmiahBidangAstronomi, AstrofisikaInstitusiInstitusi Carnegie untuk SainsUniversitas San Francisco StateUniversitas California, BerkeleyPembimbing doktoralSteven S. Vogt [1] Geoffrey W. Marcy (lahir 29 September 1954, St. Clair S...

Passo del CerroIl cartello posto in cima al passo.Stato Italia Regione Emilia-Romagna Provincia Piacenza Località collegateVal Trebbia e Val Nure Altitudine750 m s.l.m. Coordinate44°47′11.03″N 9°33′08.37″E44°47′11.03″N, 9°33′08.37″E Pendenza massimaVersante da Bettola 8,5 %Versante da Perino di Coli 12[1]% LunghezzaVersante da Bettola 7,2 kmVersante da Perino di Coli 13,5 km Chiusura invernaleno Mappa di localizzazionePasso del C...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 孝恩寺 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2021年12月) 孝恩寺 観音堂(国宝)所在地 大阪府貝塚市木積798�...







