Fractal in soil mechanics

A fractal is an irregular geometric object with an infinite nesting of structure at all scales. It is mainly applicable in soil chromatography and soil micromorphology (Anderson, 1997). Internal structure, pore size distribution and pore geometry can be identified by using fractal dimension at nano scale. As soil is heterogeneous the pore spaces are made up of macropores, micropores and mesopores. When soil is studied in nanoscale it the macropore are composed of micro and meso pore and further they are composed of organo-mineral complex.

The fractal approach to soil mechanics is a new line of thought. It was first raised in "Fractal Character Of Grain-Size Distribution Of Expansion Soils" by Yongfu Xu and Songyu Liu, published in 1999, by Fractals. There are several problems in soil mechanics which can be dealt by applying a fractal approach. One of these problems is the determination of soil-water-characteristic curve (also called (water retention curve) and/or capillary pressure curve). It is a time-consuming process considering usual laboratory experiments. Many scientists have been involved in making mathematical models of soil-water-characteristic curve (SWCC) in which constants are related to the fractal dimension of pore size distribution or particle size distribution of the soil. After the great mathematician Benoît Mandelbrot—father of fractal mathematics—showed the world fractals, Scientists of Agronomy, Agricultural engineering and Earth Scientists have developed more fractal-based models. All of these models have been used to extract hydraulic properties of soils and the potential capabilities of fractal mathematics to investigate mechanical properties of soils. Therefore, it is really important to use such physically based models to promote our understanding of the mechanics of the soils. It can be of great help for researchers in the area of unsaturated soil mechanics. Mechanical parameters can also be driven from such models and of course it needs further works and researches. Fractal calculus is a framework that includes functions with fractal support.

References

  • Anderson, A.N., McBratney, A.B. and Crawford, J.W., 1997. Applications of fractals to soil studies. In Advances in Agronomy (Vol. 63, pp. 1-76). Academic Press.


Stub icon

This soil science–related article is a stub. You can help Wikipedia by expanding it.

Stub icon

This hydrology article is a stub. You can help Wikipedia by expanding it.

Read other articles:

Kanada

Halaman ini berisi artikel tentang negara di Amerika Utara. Untuk bahasa di India, lihat Bahasa Kannada. KanadaCanada (Inggris dan Prancis) Bendera Lambang Semboyan: A mari usque ad mare (Latin)Dari Laut ke LautLagu kebangsaan:  O Canada (Oh Kanada) Lagu kerajaan:  God Save the King (Tuhan Jaga sang Raja) Perlihatkan BumiPerlihatkan peta BenderaIbu kotaOttawa45°24′N 75°40′W / 45.400°N 75.667°W / 45.400; -75.667Kota terbesarToronto 45°42′N 79°...

 

Penguin Books

Penguin BooksPerusahaan indukPenguin Random House (per 1 Juli 2013)[1]StatusAktifDidirikan1935; 89 tahun lalu (1935)PendiriAllen Lane, Richard Lane, John LaneNegara asalBritania RayaKantor pusatCity of Westminster, London, InggrisDistribusiBritania Raya, Republik Irlandia, India, Amerika Serikat, Australia, Afrika Selatan, KanadaTokoh kunciPeter Field, CEO Madeline McIntosh, Presiden (AS)Jenis terbitanBukuImprintPenguin Classics, Viking PressPemilikBertelsmann, Pearson PLCSitus r...

 

تومي تايلور (لاعب كرة قدم بريطاني)

  لمعانٍ أخرى، طالع تومي تايلور (توضيح). تومي تايلور   معلومات شخصية الميلاد 26 سبتمبر 1951 (العمر 72 سنة) مركز اللعب مدافع الجنسية المملكة المتحدة  معلومات النادي النادي الحالي Europa Point F.C. [الإنجليزية]‏ المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1966–1970 ليتون أورينت 114 (4) ...

العلاقات البوتانية القيرغيزستانية

العلاقات البوتانية القيرغيزستانية بوتان قيرغيزستان   بوتان   قيرغيزستان تعديل مصدري - تعديل   العلاقات البوتانية القيرغيزستانية هي العلاقات الثنائية التي تجمع بين بوتان وقيرغيزستان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية ل�...

 

Paus Marinus II

Marinus IIAwal masa kepausan30 Oktober 942Akhir masa kepausanMei 946PendahuluStefanus VIIIPenerusAgapetus IIInformasi pribadiNama lahir???Lahir???Roma, ItaliaWafatMei 946Roma, Italia Paus Marinus II (atau Martinus III), lahir di Roma, merupakan seorang Paus dari tahun 942 sampai 946. Ia diangkat menjadi paus melalui campur tangan Alberico II (932–954) dari Spoleto dan berkonsentrasi pada aspek administratif kepausan.[1] Referensi ^ Imma Penn, Dogma Evolution and Papal Fallacies, (Au...

 

بوابة:عقد 1990

مرحبا بكم في بوابة عقد 1990   عقد 1990 بدأ في غُرّة يناير 1990 وانتهى في آخر يوم من ديسمبر 1999 عقد 19901990-1999 تصفَّح بوَّابات أُخرى تحديث مُحتويات هذه الصفحة   حدث بارز ⇧ ✎  👈 الغزو العراقي للكويت هجوم شنه الجيش العراقي على الكويت في 2 أغسطس 1990 استغرقت العملية العسكرية يومي�...

Masami Kurumada

Masami KurumadaLahir6 Desember 1953 (umur 70)Tsukishima, Chūō, TokyoKebangsaan JepangPekerjaanmangakaSitus webOfficial website Bagian dari seri tentangAnime dan manga Anime Sejarah Industri Animasi net orisinal Animasi video orisinal Fansub Fandub Perusahaan Seri terpanjang Daftar Manga Sejarah Pasar internasional Mangaka Dōjinshi Scanlation Alternatif Gekiga Yonkoma Penerbit Seri terlaris Seri terpanjang Daftar Kelompok demografi Anak-anak Dewasa Shōnen Shōjo Seinen Josei Genre Ba...

 

William A. Russell (Massachusetts politician)

American politician William A. RussellMember of theU.S. House of Representatives from MassachusettsIn officeMarch 4, 1879 – March 3, 1885Preceded byBenjamin ButlerSucceeded byCharles Herbert AllenConstituency7th district (1879–83)8th district (1883–85)Member of the Massachusetts House of RepresentativesIn office1869 Personal detailsBorn(1831-04-22)April 22, 1831Wells River, VermontDiedJanuary 10, 1899(1899-01-10) (aged 67)Boston, MassachusettsResting placeBellevue Cemetery...

 

Edoardo Albinati

Edoardo Albinati alla Fiera internazionale del libro di Santiago 2018 Premio Strega 2016 Edoardo Albinati (Roma, 11 ottobre 1956) è uno scrittore, traduttore e sceneggiatore italiano. Indice 1 Biografia 2 Opere letterarie 2.1 Romanzi 2.2 Racconti 2.3 Prose autobiografiche 2.4 Poesia 2.5 Saggi 3 Sceneggiature cinematografiche 4 Note 5 Altri progetti 6 Collegamenti esterni Biografia Nato e residente a Roma, ha studiato al Liceo classico San Leone Magno (dove è ambientato il suo romanzo La scu...

Tyrrhenian Basin

The Tyrrhenian Basin is a sedimentary basin located in the western Mediterranean Sea under the Tyrrhenian Sea. It covers a 231,000 km2 area that is bounded by Sardinia to the west, Corsica to the northwest, Sicily to the southeast, and peninsular Italy to the northeast. The Tyrrhenian basin displays an irregular seafloor marked by several seamounts and two distinct sub-basins - the Vavilov and Marsili basins. The Vavilov deep plain contains the deepest point of the Tyrrhenian basin at ap...

 

Crater Lake National Park

National park in Oregon Crater Lake National ParkIUCN category II (national park)Panoramic view of Crater LakeLocation in OregonShow map of OregonLocation in the United StatesShow map of the United StatesLocationKlamath County, Oregon, United StatesNearest cityKlamath FallsCoordinates42°54′43″N 122°08′53″W / 42.91183°N 122.14807°W / 42.91183; -122.14807Area183,224 acres (741.48 km2)[1]EstablishedMay 22, 1902 (1902-05-22)Vis...

 

Cane lupino del Gigante

Questa voce o sezione sull'argomento cani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Questa voce o sezione sull'argomento zoologia non è ancora formattata secondo gli standard. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Cane lupino del GiganteNome originaleCane luvin, Cane ...

末沙布

尊敬的拿督斯里莫哈末·沙布Mohamad bin Sabu国会议员2018年9月24日末沙布在五角大楼与美国国防部长詹姆斯·马蒂斯会面农业及食品工业部部长现任就任日期2022年12月3日君主最高元首苏丹阿都拉最高元首苏丹依布拉欣·依斯迈首相安华·依布拉欣副职陈泓缣（2022年至2023年）亚瑟古律（2023年至今）前任羅納建迪国防部长任期2018年5月21日—2020年2月24日君主最高元首端姑莫哈末五世...

 

Державний комітет телебачення і радіомовлення України

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна  УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

 

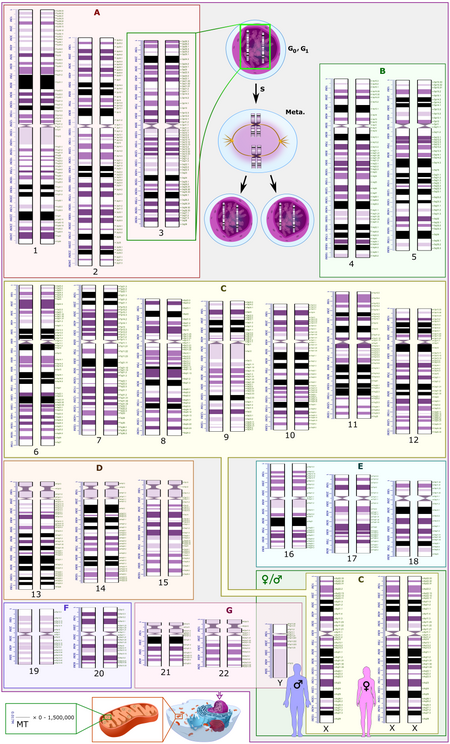
Kariotipe

Kariogram laki-laki menggunakan pewarnaan Giemsa Kariotipe adalah proses pengambilan foto kromosom untuk menentukan komplemen kromosom individu, termasuk jumlah kromosom dan kelainan apa pun. Istilah ini juga digunakan untuk set kromosom lengkap dalam suatu spesies atau organisme individu[1] dan untuk tes yang mendeteksi komplemen ini atau mengukur jumlahnya. Kariotipe menggambarkan jumlah kromosom suatu organisme dan seperti apa bentuk kromosom ini di bawah mikroskop cahaya. Perhatia...

The Poor Man's Guardian

Poor Man’s Guardian, 13 August 1831 The Poor Man's Guardian adalah surat kabar mingguan murah yang diterbitkan di London, Inggris, oleh Henry Hetherington sejak Juli 1831 sampai Desember 1835. Hetherington menerbitkan Poor Man's Guardian, pengganti harian murah Penny Papers for the People miliknya tahun 1830-31, sebagai tantangan langsung bagi pemerintah. Dengan harga satu penny untuk tiap terbitannya, koran ini memiliki slogan yang jelas: Published contrary to 'law' to try the power of 'mi...

 

OTAN

«NATO» redirige aquí. Para otras acepciones, véase Nato. Organización del Tratadodel Atlántico Norte(en inglés) North Atlantic Treaty Organization(en francés) Organisation du traité de l'Atlantique nord Bandera Insignia Lema: «Animus in consulendo liber»[1]​(en latín: «Espíritu libre para decidir») Himno: Himno de la OTAN Actuales Estados miembros de la OTANActuales Estados miembros de la OTAN   Sede Bruselas, Bélgica Idiomas oficiales Inglés y francés[2]​ T...

 

Four seasons altar of Würzburg

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Four seasons altar of Würzburg – news · newspapers · books · scholar · JSTOR (January 2014) (Learn how and when to remove this message) Summer cherub Autumn cherub A Roman decorated altar dating from early in the reign of Claudius (around AD 40) is known as the Four seasons alt...

1918 Norwegian Football Cup

Football tournament season 1918 Norwegian Football CupNorgesmesterskapet i fotball for menn 1918Tournament detailsCountryNorwayTeams44Defending championsSarpsborgFinal positionsChampionsKvik (Fredrikshald) (1st title)Runner-upBrannTournament statisticsMatches played42← 19171919 → The 1918 Norwegian Football Cup was the 17th season of the Norwegian annual knockout football tournament. The tournament was open for all members of NFF. Kvik (Fredrikshald) won their first...

 

Liste des cantons de l'Isère

Découpage cantonal du département de l'Isère, avec en surimpression les arrondissements (en nuances de bleu) - Carte arrêtée au 1er janvier 2019. Le département de l'Isère compte 29 cantons, répartis dans 3 arrondissements. Le département comptait 58 cantons de l'Isère jusqu'à la veille des élections départementales de mars 2015. Depuis ce scrutin, le département ne compte plus que 29 cantons[1]. Histoire Découpage cantonal antérieur à 2015 Arrondissement Cantons Arrondisseme...