Eulerian number
|
Read other articles:

Influential female Chinese pirate Zheng Yi Sao (Pirate)鄭一嫂Zheng Yi Sao in an 1836 illustrationBornShi Yang (石陽)Shi Xianggu (石香姑)1775 (1775)Xinhui, Guangdong, Qing ChinaDied1844 (aged 68–69)Nanhai, Guangdong, Qing ChinaNationalityChineseOccupation(s)Pirate leader and gambling house ownerCriminal chargePiracyCriminal statusPacifiedSpouses Zheng Yi (m. 1801; died 1807) Zhang Bao (m. 18...

Isländska köket LandIslandNationalrättHákarlParadrätterSkyr, hangikjötViktiga stapelvarorLammkött, Skaldjur En fiskares skjul i Reykjavik 1835, med fisk hängande utanför för torkning. Lufttorkad fisk är populärt på Island. Det isländska köket domineras av lamm, mjölkprodukter och fisk genom Islands närhet till havet. Bland vanliga maträtter i Island märks till exempel skyr, hangikjöt, kleinur, laufabrauð och bollur. Þorramatur är en traditionell buffé som serveras på ...

Tua Tua KeladiAlbum kompilasi (singel) karya Anggun C. SasmiDirilis23 Januari 1990Direkam15 April 1990GenreHard Rock, Heavy Metal, Rock 'n' roll, Balada, Glam Metal, Pop remaja, Pop Rock, New waveLabelAtlantic Recordskompilasi singel Anggun C. Sasmi Mimpi(1989)Mimpi1989 Tua Tua Keladi(1990) Laba Laba(1991)Laba Laba1991 Tua Tua Keladi adalah sebuah album kompilasi karya Anggun C. Sasmi yang dirilis pada tahun 1990. Album ini bukanlah album solo Anggun karena ia hanya menyanyi...

AirportPlymouth Municipal AirportA private plane on the airport's main rampIATA: PYMICAO: KPYMFAA LID: PYMSummaryAirport typePublicOwnerTown of PlymouthServesPlymouth County, MassachusettsElevation AMSL148 ft / 45 mCoordinates41°54′32″N 070°43′44″W / 41.90889°N 70.72889°W / 41.90889; -70.72889Websitepymairport.comMapStatistics (2009)Aircraft operations73,040Based aircraft134Source: Federal Aviation Administration[1] Plymouth Municipal...

2011 2021 Élections départementales de 2015 dans le Territoire de Belfort 18 sièges au sein du conseil départemental les 22 et 29 mars 2015 Type d’élection Élections départementales Campagne Du 9 mars 2015 au 21 mars 2015 Du 23 mars 2015 au 28 mars 2015 Corps électoral et résultats Population 146 935 Inscrits au 1er tour 95 135 Votants au 1er tour 51 681 54,32 % Votes exprimés au 1er tour 48 785 Votes blancs au 1er tour 1 757 Votes nuls...

US military training and research group Defense Equal Opportunity Management Institute (DEOMI)Headquarters366 Tuskegee Airmen Drive,Patrick Space Force BaseFloridaWebsitewww.deomi.org The Defense Equal Opportunity Management Institute (DEOMI) is a U.S. Department of Defense joint services school and research laboratory located at Patrick Space Force Base, Florida, offering both resident and off-site courses, and working in areas of equal opportunity, intercultural communication, religious, ra...

SMAN 1 Marga TigaInformasiDidirikan2002JenisNegeriAkreditasiBNomor Statistik Sekolah301120404010Nomor Pokok Sekolah Nasional10805994Kepala SekolahMei Linawati, S.Pd., M.MKetua KomiteIsmailRentang kelas10 - 12StatusNegeriAlamatLokasiJl. Raya Negeri Tua, Lampung Timur, Lampung, IndonesiaKoordinatL= 5.1309, B= 105.5246Situs websmamargatiga.sch.idSurelsmamargatiga@gmail.comMotoMotoDisiplin, Berahlak Mulia dan Berprestasi SMA Negeri 1 Marga Tiga adalah sekolah negeri yang berada di ...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Untuk kegunaan lain, lihat Ali Akbar Khan (disambiguasi). Ali Akbar KhanInformasi latar belakangLahir(1922-04-14)14 April 1922AsalComilla, Bengal Timur (sekarang Bangladesh)Meninggal18 Juni 2009(2009-06-18) (umur 87)San Anselmo, California, Amerika SerikatGenreMusik klasik HindustaniPekerjaanKomponis, SarodiyaInst...

Dr. H.Dede YusufS.T., M.I.Pol. Wakil Gubernur Jawa Barat ke-11Masa jabatan13 Juni 2008 – 13 Juni 2013GubernurAhmad HeryawanPendahuluNu'man Abdul HakimPenggantiDeddy MizwarAnggota Dewan Perwakilan RakyatRepublik IndonesiaPetahanaMulai menjabat 1 Oktober 2014Perolehan suara142.939 (2009)165.182 (2014)Daerah pemilihanJawa Barat IIMasa jabatan1 Oktober 2004 – 13 Juni 2008Perolehan suara28.331 (2004)PenggantiNina Mardiana[1]Daerah pemilihanJawa Barat IX Inform...

Public university in River Falls, Wisconsin, US UWRF redirects here. For the literary festival in Bali, see Ubud Writers and Readers Festival. University of Wisconsin–River FallsFormer namesRiver Falls State Normal School (1874–1927)River Falls State Teachers College (1927–1951)Wisconsin State College–River Falls (1951–1964)Wisconsin State University-River Falls (1964–1971)MottoGlobal. Innovative. Excellent.TypePublic universityEstablished1874; 150 years ago (187...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Questa voce sugli argomenti arene di pallacanestro degli Stati Uniti d'America e stadi del ghiaccio è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Questa voce sull'argomento architetture di Boston è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. TD GardenThe Garden, The Vault Informazioni generaliStato Stati Uniti Ubicazione100 Legends WayBoston, Massachusetts 02114 Inizio lavorimaggio 1993 Inaugurazione30...

Cet article est une ébauche concernant une chanson en langue française, le Concours Eurovision de la chanson et la Belgique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Avanti la vie Chanson de Jacques Zegers au Concours Eurovision de la chanson 1984 Sortie 1984 Langue Français Genre Chanson française Auteur Jacques Zegers Compositeur Henri Seroka Chansons représentant la Belgique au Concours Eurov...

Peru beauty pageant title Miss Grand PeruFormation2014TypeBeauty pageantHeadquartersLimaLocationPeruMembership Miss Grand InternationalOfficial language SpanishNational directorJessica NewtonParent organizationGrupo D'Elite(2016 – Present) Miss Grand Peru is a national beauty pageant title bestowed upon a woman chosen to represent Peru at the annual international pageant, Miss Grand International.[1][2][3] The title was first mentioned in 2014 when a finali...

Moscow Metro station AnninoАнниноMoscow Metro stationGeneral informationLocationChertanovo Yuzhnoye District, Southern Administrative OkrugMoscowRussiaCoordinates55°34′58″N 37°35′48″E / 55.5828°N 37.5966°E / 55.5828; 37.5966Owned byMoskovsky MetropolitenLine(s) Serpukhovsko-Timiryazevskaya linePlatforms1 island platformTracks2ConnectionsBus: 118, 249, 668, 819Trolleybus: 40ConstructionStructure typeShallow single-vaultDepth9Platform levels1Parkin...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

لمعانٍ أخرى، طالع نيو سالم (توضيح). نيو سالم الإحداثيات 42°30′15″N 72°19′57″W / 42.504166666667°N 72.3325°W / 42.504166666667; -72.3325 [1] تاريخ التأسيس 1737 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة فرانكلين خصائص جغرافية ال...

Railway station in Sydney, New South Wales, Australia CronullaT set waiting at Cronulla railway station in May 2019General informationLocationCronulla Street, CronullaCoordinates34°03′20″S 151°09′05″E / 34.055648°S 151.151472°E / -34.055648; 151.151472Elevation13 metres (43 ft)Owned byTransport Asset Holding EntityOperated bySydney TrainsLine(s)CronullaDistance34.81 km (21.63 mi) from CentralPlatforms2 (1 side)Tracks4ConnectionsBusConstructio...

Prison farm in Texas This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (September 2022) (Learn how and when to remove this message) W. F. Ramsey UnitLocation1100 FM 655 Rosharon, Texas 77583Coordinate...
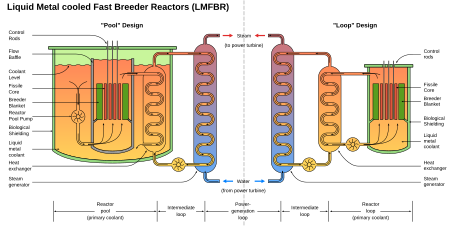
Indian fast breeder nuclear reactor design PFBRGenerationPrototypeReactor conceptSodium-cooled fast reactorReactor lineIFBR (Indian fast-breeder Reactor)Designed byIGCARManufactured byBHAVINIStatusCompleted[1]Main parameters of the reactor coreFuel (fissile material)232Th/235U[2][3]Fuel stateSolidNeutron energy spectrumFastPrimary control methodControl rodsPrimary coolantLiquid sodiumReactor usagePrimary useBreeding of 233U for AHWR-300 and generati...


























































![{\displaystyle \left\langle \!\!\left\langle {0 \atop k}\right\rangle \!\!\right\rangle =[k=0].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cda001a9301196dab5512d11ab97ce842dae3cd)







