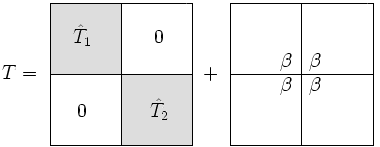
Divide-and-conquer eigenvalue algorithm
|
Read other articles:

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (July 2019) Brac SystemsIndustryWater reclamationFoundedFebruary 2005; 19 years ago (2005-02) in Montreal, CanadaFounderDennis YasarDefunct2012 (2012)FatePurchased by Greyter Water SystemsProductsGreywater, rainwater, blackwater recycling systemsWebsitegreyter.com (Greyter's website) Brac Systems, Inc assets ...

GTRE GTX-35VS Kaveri adalah turbofan afterburning yang dikembangkan oleh Gas Turbine Research Establishment (GTRE), sebuah laboratorium di bawah DRDO di Bangalore, India. Sebuah desain India, Kaveri pada awalnya ditujukan untuk model produksi kekuatan tempur HAL Tejas, juga dikenal sebagai Light Combat Aircraft (LCA) sedang dibangun oleh Aeronautical Development Agency. Namun, program Kaveri gagal untuk memenuhi persyaratan teknis yang diperlukan atau mengikuti jadwal dibayangkan dan secara ...

Komando Daerah Militer saat ini dipimpin oleh seorang Panglima Kodam (Pangdam) yang berpangkat Mayor Jenderal. No Komando Foto Nama Alumni Korps Sejak Menjabat Lama Menjabat Jabatan Sebelumnya 1. Kodam I/Bukit BarisanDaftar Pangdam Mochammad Hasan Akmil 1989 Infanteri (Kopassus) 21 Agustus 2023 (SK: 17 Juli 2023)[1] 7 bulan dan 2 hari Asisten Teritorial Kepala Staf Angkatan Darat 2. Kodam II/SriwijayaDaftar Pangdam Yanuar Adil Akmil 1988 Kavaleri 21 Agustus 2023 (SK: 17 Juli...

Anxiolytic drug FabomotizoleClinical dataTrade namesAfobazoleOther namesObenoxazineRoutes ofadministrationOralLegal statusLegal status US: Unscheduled Not FDA approved Pharmacokinetic dataBioavailability43.64%, pronounced first-pass effectMetabolismextensive hepaticOnset of action0.85±0.13 hoursElimination half-life0.82±0.54 hoursIdentifiers IUPAC name 4-[2-[(6-ethoxy-1H-benzimidazol-2-yl)sulfanyl]ethyl]morpholine CAS Number173352-21-1PubChem CID9862937DrugBankDB13623ChemSpider803...

German psychiatrist (1856–1926) Emil KraepelinEmil Kraepelin in his later yearsBorn(1856-02-15)15 February 1856Neustrelitz, Grand Duchy of Mecklenburg-Strelitz, German ConfederationDied7 October 1926(1926-10-07) (aged 70)Munich, Bavaria, Weimar GermanyNationalityGermanAlma materLeipzig UniversityUniversity of Würzburg(MBBS, 1878)Ludwig Maximilian University of Munich(Dr. hab. med., 1882)Known forClassification of mental disorders, Kraepelinian dichotomySpouseIna Marie Marie ...

1933 film by Rouben Mamoulian The Song of SongsTheatrical release posterDirected byRouben MamoulianScreenplay by Leo Birinski and Samuel Hoffenstein Based onfrom the novel by Hermann Sudermannand the play byEdward SheldonStarring Marlene Dietrich Brian Aherne Lionel Atwill Alison Skipworth CinematographyVictor MilnerMusic by Karl Hajos Herman Hand Bernhard Kaun Milan Roder(all uncredited) Distributed byParamount PicturesRelease date July 19, 1933 (1933-07-19) (United States...

French composer and pianist (1866–1925) Satie in 1920 by Henri Manuel Eric Alfred Leslie Satie[n 1] (17 May 1866 – 1 July 1925), who signed his name Erik Satie after 1884, was a French composer and pianist. He was the son of a French father and a British mother. He studied at the Paris Conservatoire, but was an undistinguished student and obtained no diploma. In the 1880s he worked as a pianist in café-cabaret in Montmartre, Paris, and began composing works, mostly f...

Marvel Comics character This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Osmosis terbalik – berita · surat kabar · buku · cendekiawan · JSTORArtikel ini perlu diterjemahkan dari bahasa Inggris ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia ...

Untuk negara klien Napoleonik dengan nama yang sama, lihat Republik Danzig. Kota Merdeka DanzigFreie Stadt Danzig (Jerman)Wolne Miasto Gdańsk (Polandia)1920–1939 Bendera Lambang Semboyan: Nec Temere, Nec TimideLagu kebangsaan: Für Danzig Danzig, yang bertetangga dengan Jerman dan Polandia.Letak Kota Merdeka Danzig di Eropa pada 1930StatusKota Merdeka di bawah perlindungan Liga Bangsa-BangsaIbu kotaDanzigBahasa yang umum digunakanJermanPolandiaAgama 64....

Swiss association Protestant Church in SwitzerlandClassificationProtestantOrientationReformedMethodistPolityA Communion of 25 regional and denominational churches that practice their own forms of church governance.AssociationsWorld Communion of Reformed ChurchesWorld Council of ChurchesConference of Churches on the RhineCommunity of Protestant Churches in EuropeRegionSwitzerlandHeadquartersBern, SwitzerlandOrigin1920[1] OltenCongregations982Members1.92 million (2022)[2]Officia...

「アプリケーション」はこの項目へ転送されています。英語の意味については「wikt:応用」、「wikt:application」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2018年4月) 古い情報を更新する必要があります。(2021年3月)出...

Global accreditation program This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Nadcap – news · newspapers · books · scholar · JSTOR (July 2015) (Learn how and when to remove this message) Nadcap (formerly NADCAP, the National Aerospace and Defense Contractors Accreditation Program) is a global cooperative accreditation program for aerospace engineering, d...

1967 British film by George Sidney Half a SixpenceOriginal American posterDirected byGeorge SidneyWritten byH. G. Wells (novel)Beverley CrossDorothy KingsleyProduced byCharles H. SchneerGeorge SidneyexecutiveJohn DarkStarringTommy SteeleJulia FosterCyril RitchardCinematographyGeoffrey UnsworthEdited byBill LewthwaiteFrank SantilloMusic byDavid HenekerProductioncompanyAmeran FilmsDistributed byParamount British PicturesRelease date 21 December 1967 (1967-12-21) Running time143 m...

Stadion De Koel Informasi stadionNama lengkapSeacon Stadion – De KoelOperatorVVV-VenloLokasiLokasiKaldenkerkerweg 1825915 AH Venlo BelandaKoordinat51°21′07″N 6°10′47″E / 51.35194°N 6.17972°E / 51.35194; 6.17972KonstruksiDibuat1972Direnovasi2004, 2007Data teknisKapasitas8.000PemakaiVVV-VenloSunting kotak info • L • BBantuan penggunaan templat ini Stadion De Koel adalah sebuah stadion serbaguna di Venlo, Belanda. Saat ini sebagian besar d...

American ultra-marathoner Kasie EnmanPersonal informationFull nameKasie Wallace-EnmanNationalityAmericanBorn (1979-09-09) 9 September 1979 (age 44) Kasie Enman (born September 9, 1979) is an American female mountain runner and ultra-marathoner. Ultra career Enman won individual bronze and team gold at the 2009 NACAC Cross Country Championships.[1] She won individual title at the 2011 World Mountain Running Championships.[2] In 2014, Enman won an event that was part o...

لنكدوك روسيون الاسم الرسمي (بالفرنسية: Languedoc-Roussillon)(بالفرنسية: Languedoc)[1] الإحداثيات 43°40′00″N 3°10′00″E / 43.666666666667°N 3.1666666666667°E / 43.666666666667; 3.1666666666667 [2] تاريخ التأسيس 4 يونيو 1960[1] سبب التسمية لانغيدوك، وروسيون تقسيم إداري البل...

Practitioner of Yoga For other uses, see Yogi (disambiguation). Bronze figure of a Yogi in Dhyana (meditation) by Malvina Hoffman This article contains Indic text. Without proper rendering support, you may see question marks or boxes, misplaced vowels or missing conjuncts instead of Indic text. A yogi is a practitioner of Yoga,[1] including a sannyasin or practitioner of meditation in Indian religions.[2] The feminine form, sometimes used in English, is yogini. Yogi has si...

Pour les articles homonymes, voir Hanson. Howard HansonBiographieNaissance 28 octobre 1896WahooDécès 26 février 1981 (à 84 ans)RochesterNationalité américaineFormation Bienen School of Music (en)Université NorthwesternUniversité MidlandActivités Chef d'orchestre, théoricien de la musique, compositeur, musicologue, pianiste, compositeur de musique classique, animateur de télévisionPériode d'activité À partir de 1916Autres informationsA travaillé pour École de musique Eas...

Russian Marxist revolutionary For the American football coach, see Leo Deutsch (American football). Leo DeutschЛев Григорьевич ДейчBorn(1855-09-26)September 26, 1855Tulchin, Podolia Governorate, Russian EmpireDiedAugust 5, 1941(1941-08-05) (aged 85)Moscow, Soviet Union Lev Grigorievich Deutsch, also known as Leo Deutsch (‹See Tfd›Russian: Лев Григорьевич Дейч) (September 26, 1855 – August 5, 1941) was a Russian Marxist revolutionary and one of fo...