Crossing Sewer

Crossing Sewer is the name of two minor streams (brooks) of the Pevensey Levels in Hailsham, Wealden District of East Sussex, England.^[1]^[2] Both streams serve as drainage ditches for several streams, many of which are unnamed.^[3]

Course

The first 776-metre (2,546 ft) long river bearing the name rises from Horse Eye Sewer and flows southwesterly. It then turns southeast and flows into White Dyke Sewer, giving rise to Lewens Sewer. The second stream, 1.8-kilometre (1.1 mi) long, comprises two ditches both rising from Rickney Sewer that eventually meet. The single drainage ditch of Crossing Sewer then drains back into White Dyke Sewer, which itself is a tributary of Down Sewer.^[1]^[3]^[4]

References

^ ^a ^b Pevensey and Cuckmere Water Level Management Board (30 October 2017). "Works Programme for 2017/18" (PDF). Water Management Alliance. p. 1. Retrieved 10 November 2022.
^ Tucker, David Gasca (2005). The Hydrological Functioning of the Pevensey Levels Wetland (PDF) (Thesis). University of London. p. 127. Retrieved 10 November 2022.
^ ^a ^b Eastbourne & Hastings: Crowborough, Battle & Heathfield (Map). 1:50,000. OS Landranger. Ordnance Survey. 14 June 2017. ISBN 9780319231449. Retrieved 10 November 2022.
^ "Crossing Sewer" (Map). Google Maps. Retrieved 10 November 2022.

50°50′47″N 0°17′13″E / 50.8464°N 0.2870°E / 50.8464; 0.2870

This article related to a river in England is a stub. You can help Wikipedia by expanding it.

Read other articles:

Sandal jepit

Sandal jepit Sandal jepit atau sandal jepang adalah sandal berwarna-warni dari karet atau karet sintetis. Tali sandal berbentuk huruf v menghubungkan bagian depan dan bagian belakang sandal. Bagian bawah sandal umumnya rata (tidak memiliki hak), sedangkan bagian atas sandal tidak memiliki penutup. Sandal jepit dipakai dengan meletakkan poros bagian depan tali sandal di antara ibu jari dan telunjuk kaki, sehingga tidak terlepas sewaktu dipakai berjalan. Selain dipakai di dalam ruang atau kamar...

Kabinet Fehrenbach

Konstantin Fehrenbach Joseph Wirth Walter Simons Otto Karl Gessler Wilhelm Groener (pada 1928) Kabinet Fehrenbach (Jerman: Kabinett Fehrenbach) adalah Reichsregierung terpilih secara demokratis keempat dari Reich Jerman. Kabinet tersebut mengambil nama dari Reichskanzler (kanselir) Konstantin Fehrenbach dan menjabat pada 25 Juni 1920 saat kabinet tersebut menggantikan kabinet Müller pertama.[1] Referensi ^ Files of the Reichskanzlei: Das Kabinett Fehrenbach I – Wahlergebnis und Reg...

Boku-boku

Boku-boku Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Incertae sedis Famili: Pomacentridae Subfamili: Pomacentrinae Genus: HemiglyphidodonBleeker, 1877[1] Spesies: Hemiglyphidodon plagiometoponBleeker, 1852[2] Sinonim[3] Glyphisodon plagiometopon Bleeker, 1852 Glyphisodon batjanensis Bleeker, 1855 Abudefduf melanopselion Fowler, 1918 Betok laguna ( Hemiglyphidodon plagiometopon ), juga dikenal sebagai boku-boku, ...

Karyme Lozano

Mexican actress (born 1978) In this Spanish name, the first or paternal surname is Lozano and the second or maternal family name is Carreno. Karyme LozanoBornKaryme Lucía Virginia Lozano Carreno (1978-04-03) April 3, 1978 (age 45)Mexico City, MexicoOther namesKaryOccupationActressYears active1994–present Karyme Lozano (Spanish pronunciation: [kaˈɾime loˈsano]; born Karyme Lucía Virginia Lozano Carreno on April 3, 1978) is a Mexican actress. She has appear...

Basilika Santo Antonius dari Padua, Manzanares

Basilika Santo Antonius dari PaduaBasilika Minor Santo Antonius dari PaduaSpanyol: Basilica San Antonio de Paduacode: es is deprecated Basilika Santo Antonius dari PaduaLokasiManzanaresNegaraKolombiaDenominasiGereja Katolik RomaArsitekturStatusBasilika minorStatus fungsionalAktif Basilika Santo Antonius dari Padua (Spanyol: Basilica San Antonio de Paduacode: es is deprecated ) adalah sebuah gereja basilika minor Katolik yang terletak di Manzanares, Kolombia. Basilika ini ditetapkan statusnya ...

The Crown, Twickenham

Pub in Twickenham, London The Crown, TwickenhamLocation within London Borough of Richmond upon ThamesGeneral informationTypePublic houseLocation174 Richmond Road, Twickenham, London TW1 (in the London Borough of Richmond upon Thames) Listed Building – Grade IIOfficial nameThe Crown Public HouseDesignated25 May 1983Reference no.1250208 The Crown is a pub at 174 Richmond Road, Twickenham, London TW1. It is a Grade II listed building, dating back to the late 18th century.[1] Refer...

Babajimi Adegoke Benson

Nigerian Politician HonourableBabajimi Adegoke BensonMember of the House of Representatives of Nigeria for Ikorodu constituencyIncumbentAssumed office June 2023 Personal detailsBorn (1972-03-30) March 30, 1972 (age 51)Ikorodu, Lagos StateNationalityNigerianPolitical partyAll Progressives Congress (Nigeria) (APC)OccupationPoliticianWebsitehttps://jimibenson.com/ Babajimi Adegoke Benson[1] is a Nigerian politician and member of the House of Representatives of Nigeria representi...

Châlons-en-Champagne

Sudut kota Châlons-en-Champagne Châlons-en-Champagne merupakan sebuah kota yang terletak di Prancis bagian timurlaut. Kota ini merupakan pusat administrasi departemen Marne dan region Champagne-Ardenne. Kota ini dulunya bernama Châlons-sur-Marne. Pada tahun 1999, kota ini memiliki jumlah penduduk 47.339 jiwa dan memiliki luas wilayah 26,05 km². Kota ini memiliki angka kepadatan penduduk 1.817 jiwa/km². Orang terkenal Nicolas Appert Nicolas Appert, penemu proses pengalengan, tahun 17...

العلاقات السنغالية الجورجية

العلاقات السنغالية الجورجية السنغال جورجيا السنغال جورجيا تعديل مصدري - تعديل العلاقات السنغالية الجورجية هي العلاقات الثنائية التي تجمع بين السنغال وجورجيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارن...

Anguilla

AnguillaAnguilla (Inggris) Bendera Lambang Semboyan: Strength and Endurance(Inggris: Kekuatan dan Ketahanan)Lagu kebangsaan: God Save the KingLagu nasional: God Bless Anguilla 1 Ibu kota(dan kota terbesar)The Valley18°13′15″N 63°03′06″W / 18.22083°N 63.05167°W / 18.22083; -63.05167Bahasa resmiInggrisPemerintahanDependensi parlementer• Raja Charles III• Gubernur Dileeni Daniel-Selvaratnam• Deputi Gubernur Perin A. Bradley�...

B

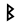
此條目介紹的是拉丁字母中的第2个字母。关于其他用法，请见「B (消歧义)」。提示：此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母（英语：ISO basic Latin alphabet）类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

Hydraotes Chaos

A region in Mars Hydraotes ChaosHydraotes Chaos, as seen by HiRISE. Click on image to see channels and layers. The scale bar is 1000 meters long.Coordinates0°48′N 35°24′W / 0.8°N 35.4°W / 0.8; -35.4 Hydraotes Chaos is a broken-up region in the Oxia Palus quadrangle of Mars, located at 0.8° North and 35.4° West. It is 417.5 km across and was named after a classical albedo feature name.[1] More information and more examples of chaos regions can be ...

46th Air Refueling Squadron

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2013) (Learn how and when to remove this message) 46th Air Refueling SquadronEmblem of the 46th Air Refueling SquadronActive1942–1996CountryUnited StatesBranchUnited States Air ForceTypeAir RefuelingGarrison/HQK. I. Sawyer AFB, MI (1961-1992)Military unit The 46th Air Refueling Squadron is an inactive ...

Royal Brunei Navy

Maritime warfare branch of Brunei's military For The historical maritime warfare of Bruneian Sultanate, see Bruneian Navy (1368-1888). Royal Brunei NavyTentera Laut Diraja BruneiBadge of Royal Brunei NavyFounded14 June 1965; 58 years ago (1965-06-14) (as the Boat Section of the Royal Brunei Armed Forces)1 October 1991; 32 years ago (1991-10-01) (as the Royal Brunei Navy)Country Brunei DarussalamAllegianceSultan of BruneiBranchNavyTypeMilitaryRoleNaval warfa...

Hollywood Blonds

Professional wrestling tag team The Hollywood Blonds is a name used by several professional wrestling tag teams over the years. The original Blonds were Buddy Roberts and Jerry Brown, who used the name in the 1970s. Rip Rogers and Ted Oates wrestled as The Hollywood Blonds in the mid-1980s in the National Wrestling Alliance's (NWA) Jim Crockett Promotions (JCP). The name was also adopted by Pretty Boy Larry Sharpe and Dynamite Jack Evans, who had a stint in then World Wide Wrestling Federatio...

Dieffenbach-au-Val

Dieffenbach-au-Valcomune Dieffenbach-au-Val – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Basso Reno ArrondissementSélestat-Erstein CantoneMutzig TerritorioCoordinate48°19′N 7°20′E / 48.316667°N 7.333333°E48.316667; 7.333333 (Dieffenbach-au-Val)Coordinate: 48°19′N 7°20′E / 48.316667°N 7.333333°E48.316667; 7.333333 (Dieffenbach-au-Val) Superficie2,96 km² Abitanti638[1] (2009) Densità215,54 ab./...

Outland Trophy

Award for the best college football interior lineman in the United States Outland TrophyAwarded forBest interior lineman in college footballCountryUnited StatesPresented byFootball Writers Association of AmericaHistoryFirst award1946Most recentT'Vondre Sweat, TexasWebsitesportswriters.net The Outland Trophy is awarded to the best college football interior lineman in the United States as adjudged by the Football Writers Association of America. It is named after John H. Outland. One of only a f...

Golden Gate, Kyiv

Historic landmark in Kyiv, Ukraine 50°26′56″N 30°30′48″E / 50.44889°N 30.51333°E / 50.44889; 30.51333 For the metro station, see Zoloti Vorota (Kyiv Metro). Golden Gate1982 reconstruction of the Golden Gate, pictured in 2018 after major renovationsGeneral informationStatusUsed as a museumTypeFortificationsAddressVolodymyrska St, 40АTown or cityKyivCountryUkraineCurrent tenantsGolden Gate MuseumConstruction started1017Completed1024OwnerNational Sanctuary So...

2014 في ألمانيا

2014 في ألمانيامعلومات عامةالسنة 2014 2013 في ألمانيا 2015 في ألمانيا تعديل - تعديل مصدري - تعديل ويكي بيانات سنوات 2012 2013 2014 2015 2016 علم ألمانيا الجدول الزمني لتاريخ ألمانيا فيما يلي قوائم الأحداث التي وقعت خلال عام 2014 في ألمانيا.[1] سياسة تعيين في المنصب 1 يناير – ألكسندر غاولاند ع...

Vitali set

Set of real numbers that is not Lebesgue measurable In mathematics, a Vitali set is an elementary example of a set of real numbers that is not Lebesgue measurable, found by Giuseppe Vitali in 1905.[1] The Vitali theorem is the existence theorem that there are such sets. Each Vitali set is uncountable, and there are uncountably many Vitali sets. The proof of their existence depends on the axiom of choice. Measurable sets Certain sets have a definite 'length' or 'mass'. For instance, th...