Read other articles:

Roddi commune di Italia Tempat categoria:Articles mancats de coordenades Negara berdaulatItaliaRegion di ItaliaPiedmontProvinsi di ItaliaProvinsi Cuneo NegaraItalia Ibu kotaRoddi PendudukTotal1.541  (2023 )GeografiLuas wilayah9,35 km² [convert: unit tak dikenal]Ketinggian284 m Berbatasan denganAlba La Morra Monticello d'Alba Santa Vittoria d'Alba Verduno SejarahSanto pelindungMaria Diangkat ke Surga Informasi tambahanKode pos12060 Zona waktuUTC+1 UTC+2 Kode telepon0173 ID ISTAT0041...

Essais Sampul depan, sekitar 1588.PengarangMichel de MontaigneJudul asliEssaisNegaraKerajaan PrancisBahasaPrancis TengahGenreEsaiPenerbitSimon Millanges, Jean RicherTanggal terbitMaret 1580TeksEssais di Wikisource Essais (bahasa Prancis diucapkan [esɛ]) atau Essays dalam bahasa Inggris, adalah esai karya Michel de Montaigne yang terdiri dari tiga buku berisi 107 bab dengan panjang yang bervariasi. Ketiga buku ini awalnya ditulis dalam bahasa Prancis Tengah dan aslinya diterbit...

1992 American filmMikeyDVD coverDirected byDennis DimsterWritten byJonathan GlassnerProduced byPeter AbramsNatan ZahaviRobert L. LevyStarring Brian Bonsall Josie Bissett Ashley Laurence John Diehl Mimi Craven Whitby Hertford Lyman Ward Lorenzo Obias CinematographyTom JewettEdited byOmer TalNatan ZahaviMusic byTim TrumanProductioncompanyTapestry FilmsDistributed byImperial EntertainmentRelease date September 23, 1992 (1992-09-23) Running time92 minutesCountryUnited StatesLanguag...

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Criminal MindsMusim 10Negara asal USAJumlah episode24RilisSaluran asliCBSTanggal tayang1 Oktober 2014 (2014-10-01)Kronologi Musim← SebelumnyaMusim 9 Daftar episode Criminal Minds Musim kesepuluh serial Criminal Minds akan tayang perda...

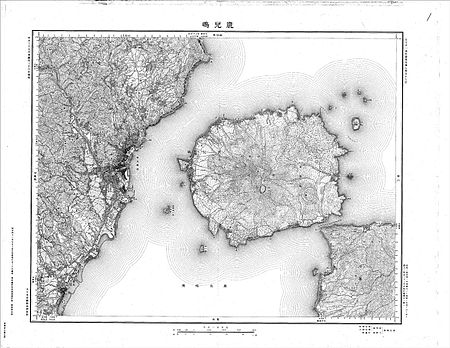
This article is about the volcano. For other uses, see Sakurajima (disambiguation). Stratovolcano in Kagoshima Prefecture, Kyushu, Japan SakurajimaView of Sakurajima from mainland Kagoshima, 2009Highest pointElevation1,117 m (3,665 ft)Coordinates31°34′50″N 130°39′29″E / 31.58056°N 130.65806°E / 31.58056; 130.65806GeographySakurajimaKagoshima Prefecture, JapanShow map of JapanSakurajimaSakurajima (Kagoshima Prefecture)Show map of Kagoshima Pre...

Untuk kegunaan lain, lihat Old Trafford. Old TraffordThe Theatre of Dreams Informasi stadionPemilikManchester UnitedOperatorManchester UnitedLokasiLokasiSir Matt Busby Way Old Trafford Greater Manchester InggrisKoordinat53°27′47″N 2°17′29″W / 53.46306°N 2.29139°W / 53.46306; -2.29139Koordinat: 53°27′47″N 2°17′29″W / 53.46306°N 2.29139°W / 53.46306; -2.29139KonstruksiMulai pembangunan1909Dibuka19 Februari 1910; 114 tahun l...

Divorce Attorney ShinPoster promosiHangul신성한, 이혼 Hanja神聖한, 離婚 Arti harfiahSacred DivorceAlih AksaraSinseonghan, ihonMcCune–ReischauerSinsŏnghan, ihon GenreLegalDramaBerdasarkanSacred Divorceoleh Kang Tae-kyungDitulis olehYoo Young-ah[1]SutradaraLee Jae-hoonLim Jun-hyukPemeranCho Seung-wooHan Hye-jinKim Sung-kyunJung Moon-sungMusikHwang Chan-heePark In-youngNegara asalKorea SelatanBahasa asliKoreaJmlh. episode4 (per 12 Maret 2023 (2023-03-12))ProduksiProdus...

Henri DaumanHenri Dauman préparant l'exposition Manhattan Darkroom au Musée Nicéphore Niépce de Chalon-sur-SaôneBiographieNaissance 5 avril 1933Paris, FranceDécès 13 septembre 2023 (à 90 ans)New York, Long IslandNationalité FrancaiseActivité Photographe, PhotojournalistePériode d'activité Depuis 1950Père Isaja DaumanMère Channa DaumanEnfant Brigitte Dauman Philippe DaumanAutres informationsA travaillé pour France-Amérique, Paris Match, Epoca, France Dimanche, L'Express, T...

American comic book series (2022-present) For other uses, see Poison ivy (disambiguation) § Comic books. Poison IvyCover to Poison Ivy #1, art by Jessica FongPublication informationPublisherDC ComicsScheduleMonthlyFormatOngoingPublication dateJune 7, 2022 – presentNo. of issues20Main character(s)Poison IvyHarley QuinnFloronic ManCreative teamWritten byG. Willow WilsonArtist(s)Marcio TakaraLetterer(s)Hassan Otsmane-ElhaouColorist(s)Arif Prianto Poison Ivy is an ongoing Ame...

Voce principale: British Academy Film Awards. I premi della 32ª edizione dei British Academy Film Awards furono conferiti nel 1979 dalla British Academy of Film and Television Arts alle migliori produzioni cinematografiche del 1978. Indice 1 Vincitori e candidati 1.1 Miglior film 1.2 Miglior regista 1.3 Miglior attore protagonista 1.4 Migliore attrice protagonista 1.5 Miglior attore non protagonista 1.6 Migliore attrice non protagonista 1.7 Migliore attore o attrice debuttante 1.8 Migliore ...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統） 哈萨克斯坦 哈萨克斯坦政府...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統） 哈萨克斯坦 哈萨克斯坦政府...

Metrolink Un tren Metrolink por San Clemente, CaliforniaDescripciónTipo Tren de cercaníasInauguración 26/10/1992Características técnicasLongitud 880 kilómetros (546,8 mi)Paradas 67ExplotaciónN.º de líneas 8Operador AmtrakMapa Notas metrolinktrains.com[editar datos en Wikidata] El Wilshire Grand Center, ubicado en Los Ángeles, es el edificio sede de Metrolink. Un tren de Metrolink en la estación de Burbank. Metrolink es un sistema de transporte ferroviario que si...

Kingdom in Western Myanmar (1429–1785) Kingdom of Mrauk-Uမြောက်ဦးဘုရင့်နိုင်ငံ1430–1785 View of Mrauk-U in the XVII centuryEarly Dutch map of Arakan (present-day Rakhine State, Myanmar, and southern part of Chittagong Division, Bangladesh)StatusVassal of Bengal Sultanate (1429–1437[1])CapitalLaunggyet (1429–1430)Mrauk U (1430–1785)Common languagesOfficial ArakaneseReligion Theravada BuddhismIslamHinduismChristianityAnimismGovern...

AirportGulkana AirportIATA: GKNICAO: PAGKFAA LID: GKNSummaryAirport typePublicOwnerState of Alaska DOT&PFServesGulkana, AlaskaElevation AMSL1,586 ft / 483 mCoordinates62°09′18″N 145°27′16″W / 62.15500°N 145.45444°W / 62.15500; -145.45444MapGKNLocation of airport in AlaskaRunways Direction Length Surface ft m 15/33 5,001 1,524 Asphalt Statistics (2006)Aircraft operations5,122Based aircraft13Source: Federal Aviation Administration[1]...

2000 in athleticsMajor world eventsOlympic GamesIAAF Athletes of the YearJan ŽeleznýMarion Jones← 1999 2001 → Overview of the events of 2000 in the sport of athletics Years in the sport of athletics ← 1997 1998 1999 2000 2001 2002 2003 → 2000 in sports Air sports American football Aquatic sports Association football Athletics Australian rules football Badminton Baseball Basketball Canadian football Chess Climbing Combat sports Sumo Cricket 1999–00 2000 2000–01 Cycling Da...

此條目需要补充更多来源。 (2024年7月18日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。致使用者：请搜索一下条目的标题（来源搜索：阿闍黎 — 网页、新闻、书籍、学术、图像），以检查网络上是否存在该主题的更多可靠来源（判定指引）。 佛教 基本教義 四圣谛 八正道 十二因缘 五蘊 緣起 空性 因果 業 戒律 毗奈耶 尸羅...

Greek and Argentine business magnate (1906–1975) Aristotle OnassisΑριστοτέλης ΩνάσηςOnassis in 1967BornAristotle Socrates Onassis(1906-01-20)20 January 1906Smyrna, Ionia, Ottoman EmpireDied15 March 1975(1975-03-15) (aged 69)Neuilly-sur-Seine, FranceResting placeSkorpios Island, GreeceCitizenshipGreeceArgentinaOccupationBusinessmanSpouses Tina Livanos ​ ​(m. 1946; div. 1960)​ Jacqueline Kennedy ​(m. 1968...

Rank theorem redirects here. For the rank theorem of multivariable calculus, see constant rank theorem. In linear algebra, relation between 3 dimensions Rank–nullity theorem The rank–nullity theorem is a theorem in linear algebra, which asserts: the number of columns of a matrix M is the sum of the rank of M and the nullity of M; and the dimension of the domain of a linear transformation f is the sum of the rank of f (the dimension of the image of f) and the nullity of f (the dimension of...