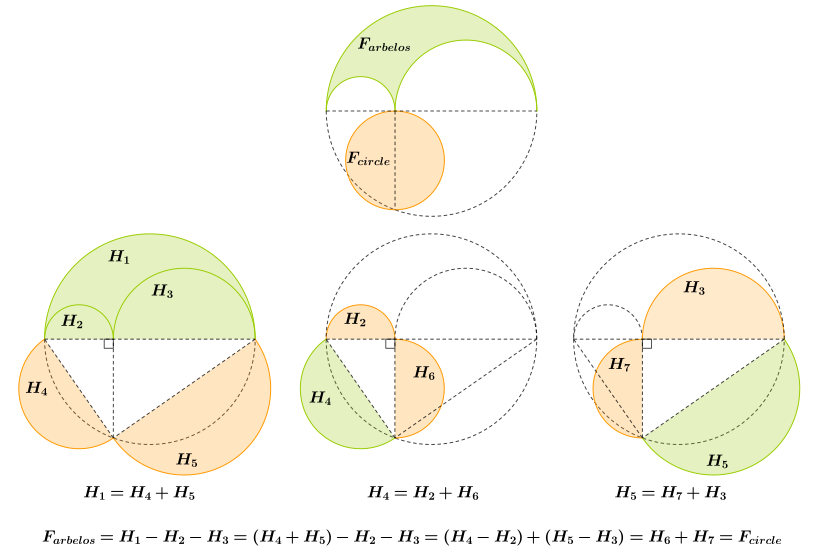
Arbelos
|
Read other articles:

Bouchaib Arroub (Arab : بوشعيب عروب ; lahir sekitar tahun 1937)[1] adalah seorang jenderal tentara Maroko. Ia menjabat sebagai Inspektur Jenderal tentara Maroko antara 13 Juni 2014 hingga Januari 2017.Bouchaib ArroubBouchaib Arroub Tahun 2014Lahir1937 (umur 86–87)MarokoPengabdian MarokoDinas/cabangAngkatan Darat MarokoLama dinas1950an–2017PangkatJenderalPerang/pertempuranUpaya kudeta Maroko 1972Gerakan HijauPerang Sahara BaratIntervensi militer ...

RAF Menwith Hill, situs yang luas di Inggris, bagian dari ECHELON dan Perjanjian UKUSA, 2005 Pesan Jerman terakhir yang berhasil dicegat oleh Britania dalam Perang Dunia II, menandakan penyerahan Jerman tanpa syarat Signals intelligence (SIGINT) adalah pengumpulan-intelijen dengan intersepsi sinyal, baik sinyal komunikasi antara orang (komunikasi intelijen - disingkat menjadi COMINT) maupun dari sinyal elektronik yang secara tidak langsung digunakan dalam komunikasi (kecerdasan elektronik- di...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ou cette section d'article est rédigé entièrement ou presque entièrement à partir d'une seule source (juillet 2017). N'hésitez pas à modifier cet article pour améliorer sa vérifiabilité en apportant de nouvelles références dans des notes de bas de page. En France, les routes départementales sont des routes gérées par les départements. Elles correspondent généralement à des liaisons ...

January 2007 storm in North America January 2007 North American ice stormCategory 2 Significant (RSI/NOAA: 3.05) TypeExtratropical cyclonesIce stormsWinter stormsFormedJanuary 11, 2007DissipatedJanuary 24, 2007 Lowest pressure961 millibars (28.4 inHg)[1] Maximum snowfallor ice accretion4 inches (10 cm) of ice (Oklahoma, Missouri), 32 inches (81 cm) of snow (Gaspe Peninsula) Fatalities85+ totalDamage$380 millionAreas affectedEastern, Central United St...

Non-commercial mass media where the general public can create content For other uses, see Public access (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (January 2022) The examples and perspective in this article deal primarily with the ...

У этого термина существуют и другие значения, см. Пинки и Брейн. Пинки и Брейнангл. Pinky and the Brain Жанры комедия, семейный, мультфильм, фантастика, приключения, пародия Техника анимации рисованная Создатели Стивен СпилбергТом Рюггер На основе Озорные анимашки Роли озву�...

ProyekWiki Perkeretaapian (Dinilai kelas templat) PerkeretaapianWikipedia:ProyekWiki PerkeretaapianTemplat:ProyekWiki PerkeretaapianArtikel perkeretaapian Portal Perkeretaapian Indonesia lbsTemplat ini berada dalam ruang lingkup ProyekWiki Perkeretaapian, salah satu proyek bersama komunitas Wikipedia yang dibuat untuk memajukan artikel bertopik Perkeretaapian dan Transportasi rel di Wikipedia. Jika Anda hendak berpartisipasi, silakan kunjungi ProyekWiki Perkeretaapian, tempat Anda dapat berg...

Count of Beaumont-le-Roger, Duke of Durazzo Louis, Duke of DurazzoCount of Beaumont-le-Roger, Duke of DurazzoArms of LouisBorn1341Died1376SpouseMaria de LizarazuJoanna, Duchess of DurazzoIssueCarlos de BeaumontHouseHouse of ÉvreuxFatherPhilip III of NavarreMotherJoan II of Navarre Louis of Évreux (also called of Navarre; 1341 – 1376) was the youngest son of Philip III of Navarre and Joan II of Navarre.[1] He inherited the county of Beaumont-le-Roger from his father (1343) and ...

American college basketball season 1973–74 Notre Dame Fighting Irish men's basketballNCAA Men's Division I Tournament, 3rd placeConferenceIndependentRankingCoachesNo. 3APNo. 5Record26–3Head coachDigger Phelps (3rd season)Assistant coachDick DiBiaso (3rd season)Captains Gary Novak (2nd year) John Shumate (2nd year) Home arenaJoyce CenterSeasons← 1972–731974–75 → 1973–74 NCAA Division I men's basketball independents standings vte Conf Overall ...

ESM TreatyTreaty Establishing the European Stability Mechanism ESM member states Other EU member statesTypeIntergovernmental agreementSigned2 February 2012 (2012-02-02)LocationBrusselsEffective27 September 2012 (2012-09-27)[1][2]ConditionRatification by signatories whose initial subscriptions represent no less than 90% of the totalPartiesAll Member States of the eurozone (20)DepositaryGeneral Secretariat of the Council of t...
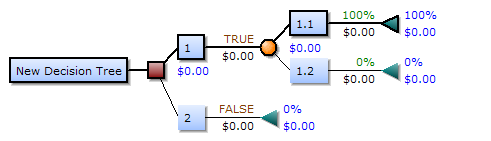
Дерево принятия решений (также называют деревом классификации или регрессионным деревом) — средство поддержки принятия решений, использующееся в машинном обучении, анализе данных и статистике. Структура дерева представляет собой «листья» и «ветки». На рёбрах («ветк...

إمارة الدرعية ← 1744 – 1818 → (Details) Kaart Algemene gegevens Hoofdstad Al-Diriyah Talen Arabisch Religie(s) Islam Munteenheid Riyal Regering Regeringsvorm Monarchie Dynastie Saoed Staatshoofd Emir Het emiraat Diriyah (Arabisch: إمارة الدرعية) was de Eerste Saoedische Staat, opgericht in het jaar 1744 toen prediker Mohammed ibn Abdul-Wahhab en prins Mohammed bin Saoed een alliantie vormden om een sociaal-religieuze hervormingsbeweging te ...

African americans making aliyah to Israel Ethnic group African Americans in IsraelTotal population25,000[1]Regions with significant populationsTel Aviv, Dimona, Jerusalem, Ein Shemer, Haifa, Ariel, Eilat ,AshkelonLanguagesEnglish, HebrewReligionJudaism, Black Israelism, Christianity.Related ethnic groupsAfrican Americans Part of a series onAfrican Americans History Periods Timeline Atlantic slave trade Abolitionism in the United States Slavery in the colonial history of the US Revolut...

Former capital city to several dynasties, now within Nanjing, China For other uses, see Jiankang (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Jiankang – news · newspapers · books · scholar · JSTOR (May 2014) (Learn how and when to remove this message) Map of Jiankang as the capital of th...

Federal electoral district of Germany 29 Cuxhaven – Stade IIElectoral districtfor the BundestagCuxhaven – Stade II in 2025StateLower SaxonyPopulation234,900 (2019)Electorate188,602 (2021)Major settlementsCuxhavenGeestlandArea2,575.3 km2Current electoral districtCreated2009PartySPDMemberDaniel SchneiderElected2021 Cuxhaven – Stade II is an electoral constituency (German: Wahlkreis) represented in the Bundestag. It elects one member via first-past-the-post voting. Under the current consti...

2021年のNPBオールスターゲーム マイナビオールスターゲーム2021ゲームデータスポンサー マイナビセ監督 原辰徳パ監督 工藤公康セ投票最多 佐藤輝明パ投票最多 吉田正尚第1戦日程 7月16日開催地 メットライフドームスコア セ・リーグ 5-4 パ・リーグMVP 菊池涼介第2戦日程 7月17日開催地 楽天生命パーク宮城スコア セ・リーグ 3-4 パ・リーグMVP 島内宏明 NPBオールスターゲ�...

فران جيفريز (بالإنجليزية: Fran Jeffries) معلومات شخصية اسم الولادة (بالإنجليزية: Frances Ann Markis) الميلاد 18 مايو 1937 بالو ألتو الوفاة 15 ديسمبر 2016 (79 سنة) لوس أنجلوس[1] سبب الوفاة سرطان مواطنة الولايات المتحدة الزوج ديك هايميس (1958–1965)ريتشارد كواين (1965...

みずの しげお水野 成夫 1948年(昭和23年)生誕 1899年(明治32年)11月13日 日本・静岡県小笠郡佐倉村死没 (1972-05-04) 1972年5月4日(72歳没)墓地 川崎市の春秋苑国籍 日本テンプレートを表示 水野 成夫(みずの しげお、1899年(明治32年)11月13日 - 1972年(昭和47年)5月4日)は、日本の実業家、文学者、翻訳家、社会運動家。フジテレビジョン(現 フジ・メディア・ホール�...

2024年 6月(水無月) 日 月 火 水 木 金 土 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 日付の一覧 各月 1 2 3 4 5 6 7 8 9 10 11 12 6月21日(ろくがつにじゅういちにち)は、グレゴリオ暦で年始から172日目(閏年では173日目)にあたり、年末まであと193日ある。 できごと ラウペンの戦い(1339) 本能寺の変(1582)。画像の寺院は現在の本能寺 シャクシャインの戦い(1...

Questa voce o sezione sull'argomento centri abitati delle Figi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Vanua LevuGeografia fisicaLocalizzazioneOceano Pacifico meridionale Coordinate16°35′S 179°11′E16°35′S, 179°11′E ArcipelagoIsole Figi Superficie5.587,1 km² Altitudine massima1.111 m s.l.m. Geografia politicaStato Figi ...