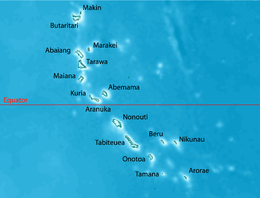
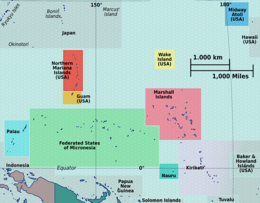
Aranuka
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Kaligrafi Basmalah Basmalah (bahasa Arab: بَسْمَلَة, basmalah; juga disebut Bi-smi llāh; بِسْمِ ٱللَّٰهِ, Dengan menyebut nama Allah,[1] atau Tasmiyyah, تَسْمِيَّة) adalah frasa dalam agama Islam yang bermakna Dengan menyebut nama Allah Yang Maha Pengasih lagi Maha Penyayang (bahasa Arab: بِسْمِ ٱللَّٰهِ ٱلرَّحْمَٰنِ ٱلرَّحِيمِ, bi-smi llāhi r-raḥmāni r-raḥīmi).[catatan 1] Bacaan ini diucapkan set...

العلاقات الأرجنتينية البريطانية المملكة المتحدة الأرجنتين تعديل مصدري - تعديل تشير العلاقات الأرجنتينية البريطانية إلى العلاقات الخارجية بين جمهورية الأرجنتين والمملكة المتحدة لبريطانيا العظمى وأيرلندا الشمالية. أسس كلا البلدين علاقاتٍ دبلوماسية في 1...

Arne Anka Arne Anka adalah komik strip Swedia yang digambar oleh Charlie Christensen dengan nama samaran Alexander Barks dari tahun 1983 sampai tahun 1995. Karakter ini mirip dengan Donal Bebek (yang disebut Kalle Anka dalam Bahasa Swedia). Kemiripannya dengan Donal hanya dalam bagian sayap, tetapi komik itu selalu berada di bar Zeke's, dimana Arne mabuk saat dia suka berpikir dengan sinis dan mendiskusikan hidup. Ini selalu terjadi di perusahaan temannya, Krille Krokodil (Krille Buaya). Char...

آنيسيوس مانليوس سيفيرنيوس بوثيوس Anicius Manlius Severinus Boëthius (باللاتينية: Anicius Manlius Torquatus Severinus Boethius)، و(باللاتينية: Boetius) معلومات شخصية اسم الولادة (باللاتينية: Anicius Manlius Severinus Boethius) الميلاد 480روما الوفاة 524 أو 525بافيا سبب الوفاة قطع الرأس مكان الدفن سان بييترو في تشي�...

Steve Kagen Steven Leslie Steve Kagen[1] (lahir 12 Desember 1949) adalah seorang politikus dan dokter Amerika Serikat yang menjadi anggota DPR dari 2007 sampai 2011. Ia adalah anggota Partai Demokrat. Referensi ^ Steven Leslie Kagen (D-Wis). Diakses tanggal 2012-04-21. Pranala luar Steve Kagen for Congress official campaign site Biografi di Biographical Directory of the United States Congress Catatan suara dikelola oleh The Washington Post Biografi, catatan suara, dan penilaian ...

Grammar school in Sydney, Australia This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (July 2021) (Learn how and when to remove this template message) This article contains content that is written like an advertisement. Please he...
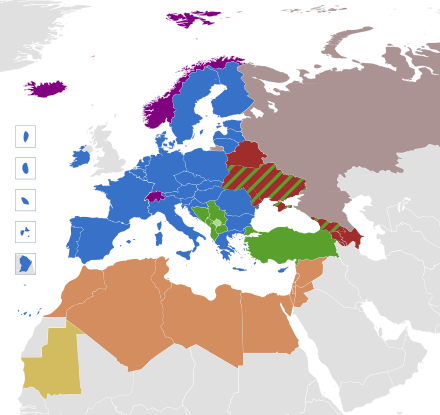
Politique européenne de voisinage (relations extérieures de l'UE) : États membres Candidats reconnus Candidats potentiels Partenariat oriental Accord de partenariat et de coopération avec la Russie États membres de l'Association européenne de libre-échange Partenariat Euromed Autres pays de l'UPM La participation de l'Union européenne aux organisations internationales est une question qui relève des relations extérieures de l'Union européenne et de la position politique selon ...

Beauty pageant Miss France 2011Laury ThillemanDate4 December 2010PresentersJean-Pierre FoucaultVenueZénith de Caen, CaenBroadcasterTF1Entrants33Placements12DebutsMiss CentreWithdrawalsMiss Albigeois Midi-Pyrénées, Artois Hainaut, Miss Béarn-Gascogne, Miss Berry Val de Loire, Miss Flandre, Miss Loire Forez, Miss Paris, Miss Quercy RouergueReturnsMiss Midi-Pyrénées, Miss New Caledonia, Miss Nord-Pas-de-CalaisWinnerLaury Thilleman BrittanyCongenialityJulie-Malika Grosse French ...

إن حيادية وصحة هذه المقالة محلُّ خلافٍ. ناقش هذه المسألة في صفحة نقاش المقالة، ولا تُزِل هذا القالب من غير توافقٍ على ذلك. (نقاش) (مايو 2016) هذه المقالة بحاجة لمراجعة خبير مختص في مجالها. يرجى من المختصين في مجالها مراجعتها وتطويرها. (مايو 2016) رأسماليةمعلومات عامةصنف فرعي من نظ...

Geometric figure The unit hyperbola is blue, its conjugate is green, and the asymptotes are red. In geometry, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfy the implicit equation x 2 − y 2 = 1. {\displaystyle x^{2}-y^{2}=1.} In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial length r = x 2 − y 2 . {\displaystyle r={\sqrt {x^{2}-y^{2}}}.} Whereas the unit circle surrounds its center, the un...

Sama Juga BohongSelebaranSutradaraChaerul UmamProduserHendrick GozaliPemeranWarkop DKI (Dono, Kasino, Indro)Ayu AzhariChintami AtmanegaraNia ZulkarnaenRina HassimIda KusumahTompoh SalvatoreMang DimanDistributorGaruda FilmTanggal rilis5 Juni 1986Durasi98 menitNegaraIndonesia Sama Juga Bohong adalah film drama komedi Indonesia yang diproduksi pada tanggal 5 Juni 1986 dan disutradarai oleh Chaerul Umam serta dibintangi antara lain oleh Warkop DKI, Ayu Azhari, Chintami Atmanegara, dan Nia Zulkarn...

География Великобритании Часть света Европа Регион Западная Европа Координаты 54° с. ш. 2° з. д. Площадь 78-я в мире 243 809 км² вода: 1,34 % суша: 98,66 % Береговая линия около 12 429 км Границы 360 км (Ирландия) Высшая точка 1344 м (Бен-Невис) Низшая точка −4 м (Восточная Англия) Крупнейша...

Pour les articles homonymes, voir Balkany. Patrick Balkany Patrick Balkany en 2019. Fonctions Maire de Levallois-Perret 23 mars 2001 – 6 mars 2020(18 ans, 11 mois et 12 jours) Élection 18 mars 2001 Réélection 22 septembre 2002mars 2008mars 2014 Prédécesseur Olivier de Chazeaux Successeur Jean-Yves Cavallini (intérim)Agnès Pottier-Dumas 13 mars 1983 – 18 juin 1995(12 ans, 3 mois et 4 jours) Élection mars 1983 Réélection mars 1989 Prédécesseur Parf...

Office in the pre-1801 Irish Parliament The Irish House of Commons in session under Speaker Pery. The Speaker of the Irish House of Commons was the presiding officer of the Irish House of Commons until its disestablishment in 1800. In the absence of a government chosen from and answerable to the Commons, the Speaker was the dominant political figure in the Parliament of Ireland. Unlike in modern British and Irish parliamentary practice, the Speaker was not expected to be politically impartial...

Book of the New Testament Part of a series onBooks of theNew TestamentPapyrus 46, one of the oldest New Testament papyri, showing 2 Cor 11:33–12:9 Gospels and Acts Four Evangelists MatthewMarkLukeJohn Lukan Acts Acts of the Apostles Epistles and Apocalypse Pauline epistles Romans 1 Corinthians2 Corinthians GalatiansEphesians PhilippiansColossians 1 Thessalonians2 Thessalonians 1 Timothy2 Timothy TitusPhilemon Hebrews Catholic epistles James 1 Peter2 Peter 1 John2 John3 John Jude A...

Papa Innocenzo IIMosaico del papa Innocenzo II nella basilica di Santa Maria in Trastevere, XII secolo.164º papa della Chiesa cattolicaElezione14 febbraio 1130 Insediamento23 febbraio 1130 Fine pontificato24 settembre 1143(13 anni e 222 giorni) Cardinali creativedi Concistori di papa Innocenzo II Predecessorepapa Onorio II Successorepapa Celestino II NomeGregorio Papareschi NascitaRoma, ? MorteRoma, 24 settembre 1143 SepolturaBasilica di Santa Maria in Trastevere Manuale...

لمعانٍ أخرى، طالع مانسفيلد (توضيح). مانسفيلد الإحداثيات 33°31′07″N 83°44′07″W / 33.51861°N 83.73528°W / 33.51861; -83.73528 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة نيوتن خصائص جغرافية المساحة 2.722197 كيلومتر مربع2.722194 كيلومتر مر...

Species of fish Ctenochaetus hawaiiensis Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Acanthuriformes Family: Acanthuridae Genus: Ctenochaetus Species: C. hawaiiensis Binomial name Ctenochaetus hawaiiensisJ. E. Randall, 1955 Ctenochaetus hawaiiensis thechevron tang, black surgeonfish, Hawaiian bristletooth, Hawaiian kole or Hawaiian surgeonfish is a species of mari...

Moscow ConferenceCodename:BRACELETHost countrySoviet UnionDate1942-08-12 – 1942-08-17Venue(s)Moscow KremlinCitiesMoscowParticipantsJoseph Stalin (USSR), Winston Churchill (UK) and Averell Harriman (United States)FollowsMoscow Conference (1941) The Second Moscow Conference (Codename: BRACELET)[1] between the major Allies of World War II took place from August 12, 1942, to August 17, 1942.[2][3] Prelude On July 30, 1942, Foreign Secretary Anthony Eden passed a message ...

此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2020年5月8日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 「马克思」重定向至此。關於其他名为马克思的人物,請見「Marx」。 卡爾·馬克思FRSA1875年摄于伦敦(图片经后人上色)出生(1818-05-05)1818年5月5日 普魯士王國特里爾逝世1883年3月14日(1883歲—03—14)(64歲) 英國英格蘭倫敦...