(2,3,7) triangle group
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2015) (Learn how and when to remove this template message) This article needs additional citations for verification. Please help improve this article by ad...

دوري ساحل العاج الممتاز 2016-17 تفاصيل الموسم دوري ساحل العاج الممتاز البلد ساحل العاج البطل أسيك أبيدجان الهابطون نادي شباب أبيدجان مباريات ملعوبة 182 عدد المشاركين 14 دوري ساحل العاج الممتاز 2015-16 دوري ساحل العاج الممتاز 2017-18 تعديل مصدري - تعديل دور�...

Venezuelan baseball player (born 1975) Baseball player Marco ScutaroScutaro during the 2012 San Francisco Giants World Champions Homecoming ParadeShortstop / Second basemanBorn: (1975-10-30) October 30, 1975 (age 48)San Felipe, VenezuelaBatted: RightThrew: RightMLB debutJuly 21, 2002, for the New York MetsLast MLB appearanceJuly 24, 2014, for the San Francisco GiantsMLB statisticsBatting average.277Home runs77Runs batted in509 Teams New York Mets (2002–200...

Bilateral relationsAustralia–Thailand relations Thailand Australia Diplomatic missionRoyal Thai Embassy, CanberraEmbassy of Australia, BangkokEnvoyArjaree SriratanabanAngela Macdonald Foreign relations exist between Australia and Thailand. Thailand is represented through its embassy in Canberra and a consulate general in Sydney. Australia has an embassy in Bangkok. Formal diplomatic relations were established between the two nations in 1952.[1] History Queensland Governor John Good...
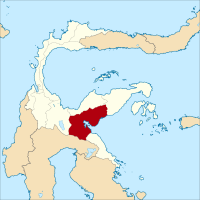
Kabupaten Morowali UtaraKabupaten LambangPetaKabupaten Morowali UtaraPetaTampilkan peta SulawesiKabupaten Morowali UtaraKabupaten Morowali Utara (Indonesia)Tampilkan peta IndonesiaKoordinat: 1°43′15″S 121°14′47″E / 1.7207°S 121.24649°E / -1.7207; 121.24649Negara IndonesiaProvinsiSulawesi TengahTanggal berdiri15 Mei 2013[1]Dasar hukumUU Nomor 12 tahun 2013[1]Hari jadi23 Oktober 2013Ibu kotaKolonodaleJumlah satuan pemerintahan Daftar Keca...

She Was PrettyGenreKomedi romantis Drama tempat kerjaDitulis olehJo Sung-heeSutradaraJung Dae-yoonPemeranHwang Jung-eum Park Seo-joon Choi Siwon Go Joon-heeNegara asalKorea SelatanBahasa asliKoreaJmlh. episode16ProduksiProduser eksekutifHan HeeLokasi produksiKoreaDurasi70 menit Rabu dan Kamis pukul 21:55 (KST)Rumah produksiBon FactoryRilis asliRilis16 September (2015-09-16) –11 November 2015 (2015-11-11) She Was Pretty (Hangul: 그녀는 예뻤다; RR: ...

American news broadcast The Situation Room with Wolf BlitzerGenreNews broadcastCountry of originUnited StatesOriginal languageEnglishProductionExecutive producers Sam Feist (2005–11) Jay Shaylor (2013–19) Emily Atkinson (2019–present) Production locationsCNN StudioWashington, D.C., U.S.Running time60 minutesOriginal releaseNetwork CNN (2005–present) Max (2023–present) ReleaseAugust 11, 2005 (2005-08-11) –present The Situation Room with Wolf Blitzer is an American news br...

Irish-American actor For other uses, see George Brent (disambiguation). George BrentBrent in 1939BornGeorge Brendan Nolan(1904-03-15)15 March 1904Ballinasloe, IrelandDied26 May 1979(1979-05-26) (aged 75)Solana Beach, California, U.S.OccupationActorYears active1924–1960, 1978Spouses Helen Louise Campbell (m. 1925; div. 1927) Ruth Chatterton (m. 1932; div. 1934) Constance Worth &#...

American high school in Missouri St. Louis University High SchoolAddress4970 Oakland AvenueSt. Louis, Missouri 63110United StatesCoordinates38°37′41″N 90°16′01″W / 38.6281°N 90.2669°W / 38.6281; -90.2669InformationSchool typePrivate secondaryMottoReligioni et Bonis ArtibusReligion and the Fine ArtsAd Majorem Dei GloriamFor The Greater Glory of GodMen for OthersReligious affiliation(s)Roman Catholic,JesuitEstablished1818; 206 years ago (181...

إسلام بناه أبادي جديد تقسيم إداري البلد إيران تعديل مصدري - تعديل إسلام بناه أبادي جديد هي قرية في مقاطعة أرومية، إيران. عدد سكان هذه القرية هو 169 في سنة 2006.[1] مراجع ^ تعداد سكان جمهورية إيران الإسلامية، 1385 / 2006. جمهورية إيران الإسلامية. مؤرشف من الأصل (إكسل) في 2010-1...

1437–38 revolt in Hungary Transylvanian peasant revoltDateJune 1437 – January 1438LocationNorth Transylvania and Tiszántúl,Kingdom of HungaryResult Patrician victoryBelligerents Transylvanian peasants and petty nobles Transylvanian aristocracyCommanders and leaders Antal Nagy de Buda †Pál Nagy de VajdaházaMihai the Vlach Ladislaus CsákiGeorge LépesMichael JakcsHenry TamásiDesiderius LosonciStrength unknown unknown The Transylvanian peasant revolt (Hungarian: erdélyi paraszt...

Pour les articles homonymes, voir Tasse (homonymie) et Tasso (homonymie). Torquato Tasso Portrait du Tasse, daté de 1577 (Fürstlich Thurn- und Taxissches Schlossmuseum, Ratisbonne, Allemagne). Données clés Nom de naissance Torquato Tasso Alias Le Tasse Naissance 11 mars 1544 Sorrente Décès 25 avril 1595 (à 51 ans) Rome Activité principale courtisan Distinctions poète lauréat Auteur Langue d’écriture italien Mouvement Humanisme Genres épopée, églogue, élégie Œuvres pri...

لا يزال النص الموجود في هذه الصفحة في مرحلة الترجمة إلى العربية. إذا كنت تعرف اللغة المستعملة، لا تتردد في الترجمة. عنتمنتخب تشيلي لكرة القدم – كأس العالم 1982 1 أوسكار ويرث 2 ليزاردو غاريدو 3 رينيه فالينزولا 4 فلاديمير بيغورا 5 فيغيروا 6 دوبو 7 إدواردو بونفاليت 8 ريفاس 9 ليتيليير...

MouïaМуя Caractéristiques Longueur 365 km Bassin 11 900 km2 Bassin collecteur la Léna Débit moyen 130 m3/s (confluence) Régime régime nivo-pluvial Cours · Coordonnées 55° 49′ 32″ N, 112° 34′ 52″ E Embouchure le Vitim Géographie Pays traversés Russie modifier La Mouïa (en russe : Муя) est une rivière de Russie qui coule en république autonome de Bouriatie en Sibérie orientale. C'est un affluent du Vitim...

Kue ulang tahun Black Forest yang ditandai dengan dekorasi ulang tahun ke-40 di atasnya, di samping lilin Ulang tahun adalah hari kelahiran seseorang, menandai hari dimulainya kehidupan di luar rahim. Dalam beberapa kebudayaan, memperingati ulang tahun seseorang biasanya dirayakan dengan mengadakan pesta ulang tahun dengan keluarga dan/atau teman. Hadiah sering diberikan pada orang yang merayakan ulang tahun. Pada saat seseorang ulang tahun, sudah menjadi kebiasaan untuk memperlakukan seseora...

South TetonSouth TetonHighest pointElevation12,519 ft (3,816 m)[1]Prominence1,074 ft (327 m)[1]Coordinates43°43′07″N 110°49′07″W / 43.71861°N 110.81861°W / 43.71861; -110.81861[2]GeographySouth TetonLocation in WyomingShow map of WyomingSouth TetonLocation in the United StatesShow map of the United States LocationGrand Teton National Park, Teton County, Wyoming, U.S.Parent rangeTeton RangeTopo mapUSGS South T...

1924 Three Mountains Press Paris edition of in our time1925 Boni & Liveright New York edition of In Our Time In Our Time adalah kumpulan cerita pendek pertama karya Ernest Hemingway yang diterbitkan pada tahun 1925 oleh Boni & Liveright, New York. Judul buku ini diambil dari Book of Common Prayer, Give peace in our time, O Lord. Sejarah penerbitan kumpulan cerpen ini cukup kompleks. Dimulai dengan enam prosa vignet yang diminta oleh Ezra Loomis Pound untuk The Little Review edisi 1923...

Metro station in Kolkata, India For the metro stations with similar names, see Dum Dum metro station. Dum Dum Cantonmentদমদম ক্যান্টনমেন্টKolkata Metro stationGeneral informationLocationSubhas Nagar, Dum Dum, Kolkata, West Bengal 700065IndiaCoordinates22°38′17″N 88°24′44″E / 22.6380°N 88.4123°E / 22.6380; 88.4123Owned byMetro Railway, KolkataOperated byMetro Railway, KolkataLine(s)Yellow LinePlatformsSide platformsTracks2Co...

This article is about the 1980s and 1990s hatchbacks. For the B-body and LX-platform variants, see Dodge Charger Daytona. For the truck variant, see Dodge Ram Daytona. Chrysler Laser redirects here. For the unrelated Plymouth vehicle based on the Mitsubishi Eclipse, see Plymouth Laser.This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dodge Dayto...

American general-interest trade book publisher Random HouseLogo used since 1998, with the 2014 Penguin Random House wordmarkCompany typeDivisionFounded1927; 97 years ago (1927)FoundersBennett Cerf, Donald KlopferHeadquartersRandom House Tower, 1745 Broadway, New York City, U.S.Area servedWorldwideKey peopleGina Centrello (president and publisher, The Random House Publishing Group)Barbara Marcus (president and publisher, Random House Children's Books)Nihar Malaviya (COO, Rand...

























