Παραγοντοποίηση
|
Read other articles:

Protein-coding gene in the species Homo sapiens SLC29A2IdentifiersAliasesSLC29A2, DER12, ENT2, HNP36, Equilibrative nucleoside transporter 2, solute carrier family 29 member 2External IDsOMIM: 602110 MGI: 1345278 HomoloGene: 37493 GeneCards: SLC29A2 Gene location (Human)Chr.Chromosome 11 (human)[1]Band11q13.2Start66,362,521 bp[1]End66,372,214 bp[1]Gene location (Mouse)Chr.Chromosome 19 (mouse)[2]Band19|19 AStart5,023,860 bp[2]End5,031,972 bp[2&...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Durio zibethinus – berita · surat kabar · buku · cendekiawan · JSTOR (Oktober 2018) Durio zibethinus Durian, Durio zibethinus Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Tugu Pensil Kulon Progo – berita · surat kabar · buku · cendekiawan · JSTOR Tugu Pensil Kulon Progoꦠꦸꦒꦸꦥꦺꦴꦠ꧀ꦭꦺꦴꦠ꧀ꦏꦸꦭꦺꦴꦤ꧀ꦥꦿꦒJenisTugu ikonikLokasiDusun Kent...
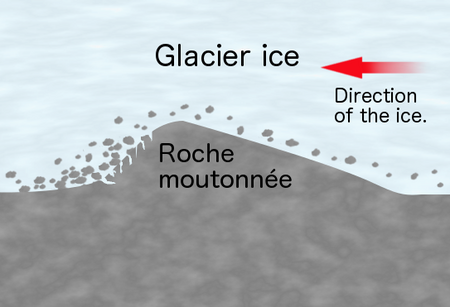
Rock formation created by the passing of a glacier Roche moutonnée near Myot Hill, Scotland In glaciology, a roche moutonnée (or sheepback) is a rock formation created by the passing of a glacier. The passage of glacial ice over underlying bedrock often results in asymmetric erosional forms as a result of abrasion on the stoss (upstream) side of the rock and plucking on the lee (downstream) side. Some geologists limit the term to features on scales of a metre to several hundred metres[1...

Abad Tiongkok (Hanzi: 中国世纪) adalah sebuah neologisme yang mengklaim bahwa abad ke-21 akan didominasi oleh Republik Rakyat Tiongkok. Ini digunakan dalam pernyataan yang menyatakan bahwa ekonomi Republik Rakyat Tiongkok akan mengambil alih posisi ekonomi Amerika Serikat sebagai ekonomi terbesar dunia.[1][2] Referensi ^ China set to be largest economy. BBC News. 2006-05-22. ^ The Chinese Century. TIME Magazine. 2007-01-22. Diarsipkan dari versi asli tanggal 2009...

United States historic placePear Lake Ski HutU.S. National Register of Historic Places Show map of CaliforniaShow map of the United StatesNearest cityLodgepoleCoordinates36°36′29″N 118°40′15″W / 36.60806°N 118.67083°W / 36.60806; -118.67083Built1939ArchitectNational Park ServiceArchitectural styleNational Park Service RusticNRHP reference No.78000285Added to NRHPMay 05, 1978[1] The Pear Lake Ski Hut (also known as Pear Lake Winter Hut...

Wilayah Budjak di Ukraina Budjak atau Budzhak adalah wilayah historis yang terletak di Oblast Odessa, Ukraina. Wilayah multietnis ini merupakan bagian selatan dari Bessarabia dan berbatasan dengan Moldova di utara dan barat, Rumania di selatan dan Laut Hitam di timur. Nama Budjak diberikan kepada wilayah ini selama dominasi Utsmaniyah (1484-1812) dan berasal dari kata dalam bahasa Turki, bucak, yang berarti pojok atau segitiga. Pranala luar (Jerman) Karte deutscher siedlungen in Bessarabien M...

Liebieghaus Depot collection storage A collection manager ensures the proper care and preservation of objects within cultural institutions such as museums, libraries, and archives. Collection managers, along with registrars, curators, and conservators, play an important role in collections care. Collection Managers and Registrars are two distinct collection roles that are often combined into one within small to mid-size cultural institutions. Collection Managers can be found in large museums ...

Form of wrestling originating in Cornwall, England Cornish wrestlingJohn Cawley throwing Chris French at Demonstration at Robby Richards Museum Opening - CWA Event 13–14 May 2006.FocusGrapplingCountry of originCornwallCreatorCornish peopleOlympic sportNo Cornish wrestling (Cornish: Omdowl Kernewek[1]) is a form of wrestling that has been established in Cornwall for many centuries and possibly longer. It is similar to the Breton Gouren wrestling style. It is colloquially known as wra...

Concept in economics A simple example of a preference order over three goods, in which orange is preferred to a banana, but an apple is preferred to an orange In economics, and in other social sciences, preference refers to an order by which an agent, while in search of an optimal choice, ranks alternatives based on their respective utility. Preferences are evaluations that concern matters of value, in relation to practical reasoning.[1] Individual preferences are determined by taste,...

American writer (1935–2019) Ward JustBornWard Swift Just(1935-09-05)September 5, 1935Michigan City, Indiana, U.S.DiedDecember 19, 2019(2019-12-19) (aged 84)Plymouth, Massachusetts, U.S.EducationTrinity CollegeGenrefictionNotable awardsAmerican Academy of Arts and Letters Ward Swift Just (September 5, 1935 – December 19, 2019)[1] was an American writer. He was a war correspondent and the author of 19 novels and numerous short stories. Biography Just was born in Michigan City, ...
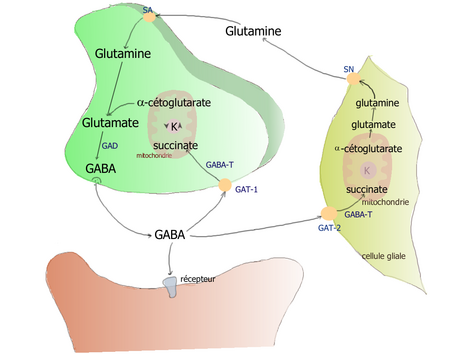
Pour les articles homonymes, voir GABA. Acide γ-aminobutyrique Structure du GABA. Identification Nom UICPA acide 4-aminobutanoïque No CAS 56-12-2 No ECHA 100.000.235 No CE 200-258-6 PubChem 119 FEMA 4288 Propriétés chimiques Formule C4H9NO2 [Isomères] Masse molaire[1] 103,119 8 ± 0,004 6 g/mol C 46,59 %, H 8,8 %, N 13,58 %, O 31,03 %, pKa 4,0459 Propriétés physiques T° fusion 203...

Loops of electric current induced within conductors by a changing magnetic field For the comic-book series, see Eddy Current (comics). For the Australian rock band, see Eddy Current Suppression Ring. Articles aboutElectromagnetism Electricity Magnetism Optics History Computational Textbooks Phenomena Electrostatics Charge density Conductor Coulomb law Electret Electric charge Electric dipole Electric field Electric flux Electric potential Electrostatic discharge Electrostatic induction Gauss ...

Les championnats d'Europe de patinage artistique sont organisés chaque année depuis 1891. Il y eut toutefois quelques années où les championnats ne purent avoir lieu : pendant plusieurs années de la Belle Époque (1896, 1897, 1903, 1904) à cause souvent du manque de glace (les championnats étant organisés sur piste naturelle, pendant et juste après la Première Guerre mondiale (de 1915 à 1921) et pendant et juste après la Seconde Guerre mondiale (de 1940 à 1946). L'édition 2...

إي جونغ هيون معلومات شخصية الميلاد 15 مايو 1990 (العمر 34 سنة)بسان, كوريا الجنوبية الجنسية بسان, كوريا الجنوبية عضو في سي إن بلو الحياة الفنية النوع موسيقى الروك، بوب الآلات الموسيقية قيثارة، بيانو، غيتار البيس، هارمونيكا آلات مميزة قيثارة، بيانو، غيتار البيس، هارمونيكا ش�...

British royal regalia Crown JewelsSt Edward's Crown is the centrepiece of the British coronation regalia.OverviewCountryUnited KingdomLocationTower of London[a]Size≈ 140 objects[2]OldestCoronation Spoon (12th century)NewestCharles III's stole (2023)Stones23,578 including Cullinan I, Cullinan II, Koh-i-Noor, Black Prince's Ruby, Stuart Sapphire, St Edward's SapphireOwnerCharles III in right of the Crown[3]ManagersCrown JewellerRoyal Collection...

Book by Bernie Sanders Bernie Sanders Guide to Political Revolution AuthorBernie SandersLanguageEnglishPublisherHenry Holt and CompanyPublication dateAugust 29, 2017Publication placeUnited StatesPages240ISBN978-1-250-13890-3 This article is part of a series aboutBernie Sanders Political positions Electoral history Early life Early career University of Chicago sit-ins Mayor of Burlington Mayoral career U.S. Representative from Vermont's at-large district Representative career CPC Elections 199...

Silent HillSilent Hill: Dying Inside coverPublication informationPublisherIDW Publishing Title(s)Dying InsideAmong the DamnedPaint it BlackThe Grinning ManDead/AliveSinner's Reward FormatsOriginal material for the series has been published as a set of limited series, graphic novels, and one-shot comics.Genre Horror Publication dateDying InsideFebruary 2004 - June 2004Among the DamnedNovember 2004Paint it BlackFebruary 2005The Grinning ManMay 2005Dead/AliveDecember 2005 - April 2006Sinner's Re...

Wolf 359 Data pengamatan Epos J2000 Ekuinoks J2000 Rasi bintang Leo Asensio rekta 10j 56m 28.99d[1] Deklinasi +07° 00′ 52.0″[1] Magnitudo tampak (V) 13.54[1] Ciri-ciri Kelas spektrum M6.5 Ve[1] Magnitudo semu (J) 7.1[1] Indeks warna U−B +1.165[2] Indeks warna B−V +2.034[2] Jenis variabel UV Ceti[3] AstrometriKecepatan radial (Rv)...

Nemzeti Bajnokság I 2020-2021OTP Bank Liga 2020-2021 Competizione Nemzeti Bajnokság I Sport Calcio Edizione 120ª Organizzatore MLSZ Date dal 14 agosto 2020al 9 maggio 2021 Luogo Ungheria Partecipanti 12 Risultati Vincitore Ferencváros(32º titolo) Retrocessioni DiósgyőrBudafok Statistiche Miglior marcatore János Hahn (22) Incontri disputati 198 Gol segnati 597 (3,02 per incontro) Cronologia della competizione 2019-2020 2021-2022 Manuale La Nemzeti Bajnokság I ...


















































