Zentripetalkraft
|
Read other articles:
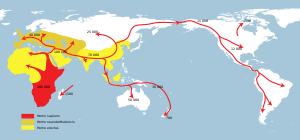
Paleo-Indians Ilustrasi manusia Paleo-Indian yang berburu glyptodontidae Heinrich Harder (1858–1935), c.1920. Kelompok manusia Paleo-Indian yang hidup pada zaman batu merupakan kelompok manusia paling awal yang mendiami daratan Amerika. Paleo-Indian, Paleoindian, atau Paleoamerika adalah suatu klasifikasi yang diberikan kepada manusia pertama yang masuk dan menghuni benua Amerika pada periode akhir zaman glasial hingga periode akhir zaman Pleistosen . Awalan paleo- berasal dari bahasa Yuna...

Sebuah akrostik tahun 1850 karya Nathaniel Dearborn, huruf pertama dari setiap baris menampilkan nama JENNY LIND Akrostik adalah sebuah bait (atau bentuk penulisan lain) dimana huruf pertama (atau silabel, atau kata) dari setiap baru (atau paragraf, atau unsur lain dalam teks tersebut) menampilkan sebuah kata, pesan, atau abjad.[1] Kata tersebut berasal dari kata Prancis acrostiche dari kata Latin pasca-klasik acrostichis, dari kata Yunani Koine ἀκροστιχίς, dari kata Yunani...

Church in Helsinki, FinlandSt. John's ChurchNya KyrkanFinnish: JohanneksenkirkkoSwedish: Johanneskyrkan60°09′42.5″N 024°56′41.0″E / 60.161806°N 24.944722°E / 60.161806; 24.944722LocationHelsinkiCountryFinlandDenominationLutheranWebsitewww.helsinginkirkot.fi/en/churches/st-johns-churchHistoryConsecrated1891 (1891)Cult(s) presentChristian LutheranArchitectureArchitect(s)Adolf Emil Melander [sv]StyleGothic RevivalGroundbreaking1888Completed18...

.lcDiperkenalkan3 September 1991Jenis TLDTLD kode negara InternetStatusAktifRegistriNIC.LCSponsorUniversitas Puerto RicoPemakaian yang diinginkanEntitas yang terhubung dengan Saint LuciaPemakaian aktualInternasional, termasuk LLC dan PLCPembatasanNone[1]StrukturRegistrasi dilakukan di tingkat kedua atau ketiga, dibawah label tingkat duaDokumennic.lcKebijakan sengketanic.lcDNSSECYaSitus webnic.lc.lc adalah top-level domain kode negara Internet untuk Saint Lucia. lbsRanah tingkat ...

Stasiun Nozawa野沢駅Stasiun Nozawa pada Oktober 2013LokasiNozawa Shimokoya Otsu 3183, Nishiaizu-machi, Yama-gun, Fukushima-ken 969-4406JepangKoordinat37°35′27″N 139°38′41″E / 37.5908°N 139.6446°E / 37.5908; 139.6446Koordinat: 37°35′27″N 139°38′41″E / 37.5908°N 139.6446°E / 37.5908; 139.6446Operator JR EastJalur■ Jalur Ban'etsu BaratLetak106.2 km dari KōriyamaJumlah peron1 peron samping + 1 peron pulauJumlah jalur3In...

Cet article est une ébauche concernant la politique et le Venezuela. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Ministère de l'Agriculture productive et des Terres Situation Type Ministère vénézuélien Organisation Ministre de l'Agriculture productive et des Terres Wilmar Castro Soteldo Site web [1] modifier Le ministère de l'Agriculture productive et des Terres (en espagnol : « minis...

Сибирский горный козёл Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКла�...

Paus Aleksander IV. Paus Aleksander IV (menjabat pada 1254-61) mengangkat dua kardinal dalam dua konsistori pada masa kepausannya.[1] Agustus 1255 Riccardo di Montecassino O.S.B. Desember 1255 Tesauro dei Beccheria O.S.B. Vall. Catatan dan referensi ^ Salvador Miranda. Cardinals of the 13th Century. The Cardinals of the Holy Roman Church. Diarsipkan dari versi asli tanggal 2019-04-15. Diakses tanggal 10 February 2019. Sumber The Cardinals of the Holy Roman Church Diarsipkan 2019...

Driverless subway line in Gyeonggi-do and Seoul, South Korea Shinbundang Line(DX Line) Shinbundang line trainOverviewNative name신분당선(新盆唐線)SinbundangseonStatusOperationalTerminiSinsaGwanggyoStations16ServiceTypeCommuter RailSystemSeoul Metropolitan SubwayOperator(s)Shinbundang Railroad Corporation, Gyeonggi Railroad Co., Ltd., New Seoul Railroad Co., Ltd., Neo TransHistoryOpened28 October 2011TechnicalLine length33.4 km (20.8 mi)Number of tracks2Track gauge1,435 ...

Questa voce o sezione sull'argomento musei d'Italia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Questa voce sull'argomento musei della Sicilia è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Museo Archeologico IbleoL'insegna del museo. UbicazioneStato Italia LocalitàRagusa IndirizzoVia Natalelli Coordina...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

R-14 Chusovaya[1] (bahasa Rusia: Чусовая) adalah rudal balistik yang dikembangkan oleh Uni Soviet selama Perang Dingin. Ini diberi nama pelaporan NATO SS-5 Skean dan dikenal oleh Grau indeks 8K65. Ini dirancang oleh Mikhail Kuzmich Yangel. Chusovaya adalah nama sebuah sungai di Rusia. Lini produksi dilakukan oleh Facility No 1001 di Krasnoyarsk. Referensi ^ Gunter's Space Page - R-14 Usovaya (SS-5, Skean) MRBM R14 | 8K65 | SS-5 | Skean at RussianSpaceWeb.com R14 at Encyclopedi...

Fourth constitution of Fiji that came into effect in 2013 See also: Constitution of Fiji Politics of Fiji Constitution History Executive President (list) Wiliame Katonivere Prime Minister Sitiveni Rabuka Cabinet Attorney-General Siromi Turaga Leader of the Opposition Inia Seruiratu Legislative Parliament Speaker: Naiqama Lalabalavu Judiciary Supreme Court Chief Justice: Kamal Kumar Court of Appeal High Court Elections Electoral system Voting Political parties Post-independence elections 1972M...

American convicted murderer and botched execution survivor Doyle HammHamm in 1981BornDoyle Lee Hamm(1957-02-14)February 14, 1957Alabama, U.S.DiedNovember 28, 2021(2021-11-28) (aged 64)Holman Correctional Facility, Atmore, Alabama, U.S.Cause of deathLymphatic cancerCriminal statusDeceasedConviction(s)Capital murderCriminal penaltyDeath (1987)DetailsKilledPatrick CunninghamWeapon.38 caliber pistol Doyle Lee Hamm (February 14, 1957 – November 28, 2021) was an American death row inmat...

Railway locomotive that produces its pulling power through a steam engine Steam railway redirects here. For the periodical, see Rail transport periodical § Steam Railway. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challeng...

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce o sezione sull'argomento competizioni calcistiche non è ancora formattata secondo gli standard. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui ...

提示:此条目页的主题不是中國—博茨瓦納關係。 關於中華民國與「波」字國家(臺灣譯名)的外交關係,詳見中波關係 (消歧義)。 中華民國—波札那關係 中華民國 博茨瓦纳 中華民國—波札那關係(英語:Botswana–Republic of China relations),是指中華民國與波札那共和國之間的關係。兩國於1966-1974年有官方外交關係,斷交後,目前沒有在對方首都互設具�...

Jalur Beijing–Guangzhou 京广铁路Kereta api Jingguang di Bukit Ular di Wuhan. Jauh di belakang, rel kereta melintasi Sungai Yangtze di atas Jembatan Wuhan.IkhtisarJenisTransportasi relSistemKereta api TiongkokStatusBeroperasiLokasiBeijing, Hebei, Henan, Hubei, Hunan, GuangdongTerminusStasiun Kereta Beijing BaratGuangzhouStasiun53 aktifOperasiOperator Kereta api TiongkokData teknisPanjang lintas2.324 km (1.444 mi)Lebar sepur1.435 mm (4 ft 8+1⁄2 in) sepu...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2015) حركة رفض حركة يمنية لمناهضة الحوثي تم تأسيسها بمحافظة إب في 17 اكتوبر 2014م، من قبل شباب ونشطاء حقوقيين وسياسيين، بهدف التصدي للانتهاكات التي ترتكبها جماعة ال...

Italian actor and film producer This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Andrea Occhipinti – news · newspapers · books · scholar · JSTOR (June 2023) (Learn how and when to remove this mes...
























































