Der Satz von Euler der Vierecksgeometrie ist ein geometrischer Lehrsatz, der eine grundlegende Identitätsgleichung über den Zusammenhang zwischen den Seitenlängen eines Vierecks und den Längen seiner beiden Diagonalen angibt. Der Satz ist einer der vielen Beiträge des großen Schweizer Mathematikers Leonhard Euler zur Elementargeometrie.
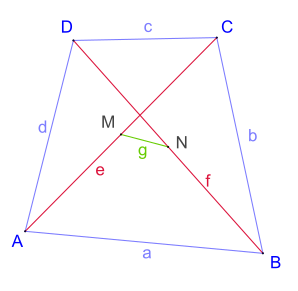 Bild zum Eulerviereck
Bild zum Eulerviereck
Der Satz lautet wie folgt:[1]
- Gegeben sei ein konvexes Viereck
 der euklidischen Ebene.
der euklidischen Ebene.
- Auf den beiden Diagonalen
 und
und  seien
seien  bzw.
bzw.  die beiden Mittelpunkte.
die beiden Mittelpunkte.
- Dann gilt:

- oder
 .
.
Folgerung
Aus dem Satz von Euler folgt unmittelbar die bekannte Parallelogrammgleichung.
Denn im Falle, dass
 ein Parallelogramm ist, folgt
ein Parallelogramm ist, folgt  , also
, also  , sowie
, sowie  und
und  und damit
und damit  oder
oder
 .
.
Hilfssatz
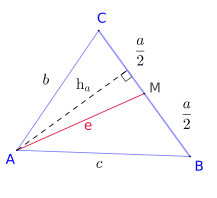 Bild zum Dreieck
Bild zum Dreieck
Der Satz von Euler lässt sich unter Zuhilfenahme des folgenden Hilfssatzes herleiten:
- Für ein Dreieck
 der euklidischen Ebene, dessen Seite
der euklidischen Ebene, dessen Seite  den Mittelpunkt
den Mittelpunkt  hat, gilt stets:
hat, gilt stets:

- oder
![{\displaystyle b^{2}+c^{2}=2\cdot \left[{\left({\frac {a}{2}}\right)^{2}+e^{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8346cb24edea11c0a7f4d9d89f125d719c91c269) .
.
Die soeben genannte Gleichung – welche offenbar eine andere Version der Apollonios-Gleichung darstellt – wurde schon von Apollonios von Perge angegeben. Sie ist auch bei Pappus Alexandrinus zu finden.[2][3]
Literatur
Weblinks
Einzelnachweise und Anmerkungen
- ↑ Friedrich Joseph Pythagoras Riecke (Hrsg.): Mathematische Unterhaltungen. Erstes Heft. 1973, S. 65
- ↑ Riecke, op. cit., S. 31, 65
- ↑ Der Hilfssatz lässt sich sowohl aus dem Satz von Stewart als auch mit dem Kosinussatz herleiten.
- ↑ Vgl. Artikel über Riecke auf Wikisource