Read other articles:

Mattia Valoti Informasi pribadiTanggal lahir 6 September 1993 (umur 30)Tempat lahir Vicenza, ItaliaTinggi 190 cm (6 ft 3 in)Posisi bermain GelandangInformasi klubKlub saat ini Monza (pinjaman dari SPAL)Nomor 10Karier junior1998–1999 Lucchese1999–2001 Cosenza2001–2002 Palermo2002–2003 Crotone2003–2004 Martina Franca2004–2006 Dalmine Futura2006–2011 AlbinoLeffeKarier senior*Tahun Tim Tampil (Gol)2010–2011 AlbinoLeffe 1 (0)2011–2014 Milan 0 (0)2011 → Albi...

A Touch of ClassPromotional film poster for A Touch of Class.SutradaraMelvin FrankProduserMelvin FrankPeter BealeRoger MooreDitulis olehMelvin FrankJack RosePemeranGeorge SegalGlenda JacksonPaul SorvinoK. CallanPenata musikJohn CameronSinematograferAustin DempsterPenyuntingBill ButlerDistributorBrunt Productions, Gordon Film Productions, Joseph Levine ProductionsTanggal rilis01 Oktober 1973 (Swedia)Durasi106 menitBahasaInggrisSpanyolIMDbInformasi di IMDb A Touch of Class adalah salah sa...

Pretty Cure (プリキュアcode: ja is deprecated , Purikyua, juga dikenal PreCure) adalah sebuah waralaba anime yang bertema magic dan seni bela diri yang dibuat oleh Izumi Todo dan diproduksi oleh ABC dan Toei Animation. Franchise Program pertama adalah Futari wa Pretty Cure yang memulai debutnya pada tahun 2004 dan dilanjutkkan dengan sekuel maupun spin off di seri berikutnya, seperti Star☆Twinkle PreCure yang sekarang ini tayang di Jepang pada tahun 2019 ini sebagai bagian dari Asahi B...

Pemandangan udara dari All England Lawn Tennis and Croquet Club All England Lawn Tennis and Croquet Club,[1] juga dikenal sebagai All England Club,[2] adalah klub anggota pribadi. Tempat ini paling dikenal sebagai tempat Kejuaraan Wimbledon, satu-satunya acara tenis Grand Slam yang masih diadakan di atas rumput. Awalnya acara amatir yang dihadiri anggota klub dan teman-teman mereka selama beberapa hari setiap musim panas, kejuaraan menjadi jauh lebih menonjol daripada klub itu...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (August 2012) (Learn how and when to remove this template message) The King's Name Tor Books hardcoverAuthorJo WaltonCover artistJulie BellCountryUnited StatesLanguageEnglishSeriesSulienGenreFantasyPublisherTor BooksPublication dateDecember 2001 (1st edition)Media ...

Perisai Salawaku. Parang Salawaku adalah sepasang senjata tradisional dari Maluku.[1] Parang Salawaku terdiri dari Parang (pisau panjang) dan Salawaku (perisai) yang pada masa lalu adalah senjata yang digunakan untuk berperang.[1] Di lambang pemerintah kota Ambon, dapat dijumpai pula Parang Salawaku.[2] Bagi masyarakat Maluku, Parang dan Salawaku adalah simbol kemerdekan rakyat.[2] Senjata ini dapat disaksikan pada saat menari Cakalele, yaitu tarian yang menyim...

Lari kayang, salah satu jenis olahraga atletik. Atletik adalah cabang olahraga berupa aktivitas fisik (jasmani) yang dinamis dan harmonis, termasuk di antaranya lari, lompat, jalan, dan lempar.[1][2] Atletik merupakan salah satu unsur dari pendidikan jasmani dan kesehatan, sebagai suatu komponen pendidikan yang mengutamakan aktivitas jasmani serta pembinaan hidup sehat dan pengembangan jasmani.[3] Atletik bermanfaat untuk meningkatkan kemampuan biomotorik, misalnya kek...

Questa voce sull'argomento contee del Wisconsin è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di DouglasconteaLocalizzazioneStato Stati Uniti Stato federato Wisconsin AmministrazioneCapoluogoSuperior Data di istituzione1854 TerritorioCoordinatedel capoluogo46°43′15″N 92°06′15″W / 46.720833°N 92.104167°W46.720833; -92.104167 (Contea di Douglas)Coordinate: 46°43′15″N 92°06′15″W / ...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند  الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

AspernstraßeLokasiDonaustadt, WinaAustriaKoordinat48°13′21″N 16°28′29″E / 48.2224°N 16.4748°E / 48.2224; 16.4748JalurSejarahDibuka2010Operasi layanan Stasiun sebelumnya   U-Bahn Wina   Stasiun berikutnya Donauspitalmenuju Karlsplatz Jalur U2Hausfeldstraßemenuju Seestadt Sunting kotak info • L • BBantuan penggunaan templat ini Aspernstraße adalah sebuah stasiun metro yang terletak di Jalur U2 di U-Bahn Wina.[1] Stasiun ini ...

Бурейская ГЭС Страна  Россия Местоположение  Амурская область Река Бурея Каскад Бурейский Собственник РусГидро Статус действующая Год начала строительства 1976 Годы ввода агрегатов 2003—2007 Основные характеристики Годовая выработка электроэнергии, млн  кВт⋅ч 71...

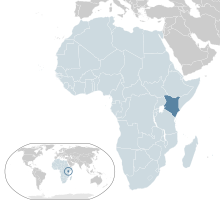
Location of Kenya Kenya is a country in East Africa and a founding member of the East African Community (EAC). Its capital and largest city is Nairobi. The capital, Nairobi, is a regional commercial hub. The economy of Kenya is the largest by GDP in East and Central Africa.[1][2] Agriculture is a major employer; the country traditionally exports tea and coffee and has more recently begun to export fresh flowers to Europe. The service industry is also a major economic driver. ...

American drama television series Six Feet UnderGenre Comedy drama[1][2][3] Black comedy[4][5] Psychological drama[1][4] Tragicomedy[6][7] Created byAlan BallStarring Peter Krause Michael C. Hall Frances Conroy Lauren Ambrose Freddy Rodriguez Mathew St. Patrick Jeremy Sisto Rachel Griffiths James Cromwell Justina Machado Theme music composerThomas NewmanComposerRichard MarvinCountry of originUnited StatesOriginal languageE...

Cricket team that represents Norway in men's international cricket This article is about the men's team. For the women's team, see Norway women's national cricket team. NorwayAssociationNorwegian Cricket BoardPersonnelCaptainKhizer AhmedInternational Cricket CouncilICC statusAssociate member[1] (2017) Affiliate member (2000)ICC regionEuropeICC Rankings Current[2] Best-everT20I 42nd 30th (16-June-2019)International cricketFirst internationalv  Austria at Seebarn Crick...

French artist and co-founder of Fauvism with Henri Matisse (1880–1954) Derain redirects here. For other uses, see Derain (disambiguation). André DerainDerain in 1903Born(1880-06-10)10 June 1880Chatou, Yvelines, Île-de-France, FranceDied8 September 1954(1954-09-08) (aged 74)Garches, Hauts-de-Seine, Île-de-France, FranceEducationAcadémie Camillo, Académie JulianKnown forPainting, sculptureMovementFauvism André Derain (/dəˈræ̃/, French: [ɑ̃dʁe dəʁɛ̃]; 10 June...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (سبتمبر 2019) وكالة الأنباء العمانية ONA وكالة الأنباء العمانية تفاصيل الوكالة الحكومية الب�...

Siege of Rethymno (1646)Part of the Cretan War (Fifth Ottoman–Venetian War)Rethymno in 17th centuryDate11 October – 13 November 1646LocationRethymno, CreteResult Ottoman victoryBelligerents  Ottoman Empire  Republic of VeniceCommanders and leaders Gazi Hüseyin Pasha Luigi MinottoStrength Unknown UnknownCasualties and losses Unknown Unknown vteCretan War (1645–1669) Crete 1st Chania Rethymno Candia 2nd Chania Dalmatia Perast Naval operations 26 May 1646 Chania Focchies 10 July...

Loss function used in robust regression In statistics, the Huber loss is a loss function used in robust regression, that is less sensitive to outliers in data than the squared error loss. A variant for classification is also sometimes used. Definition Huber loss (green, δ = 1 {\displaystyle \delta =1} ) and squared error loss (blue) as a function of y − f ( x ) {\displaystyle y-f(x)} The Huber loss function describes the penalty incurred by an estimation procedure f. Huber (1964...

Salishan ethnic group of British Columbia, Canada This article is about the ethnic group. For their language, see Nuxalk language. This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Nuxalk – news · newspapers · books · scholar · JSTOR (April 2014) Ethnic group Bella Coola (Nuxalk Nation)NuxalkNuxálk ...

Continuously computed dead reckoning This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (September 2023) A 1950s inertial navigation control developed at MIT Comparison of accuracy of various navigation systems: the radius of the circle indicates the accuracy. A smaller radius corresponds to a higher accuracy An inertial navigation system (INS; also i...