Quantorenelimination
|
Read other articles:

Chelmsford Shire Hall Population 111.511 (Sensus 2011)[1] Ref. grid OS TL713070 District Chelmsford County shire Essex Wilayah Negara konstituen Inggris Negara berdaulat Britania Raya Kota pos CHELMSFORD Distrik kode pos CM1, CM2, CM3 Kode telepon 01245 Polisi Pemadam kebakaran Ambulans Parlemen UE Inggris Timur Parlemen Britania Chelmsford Daftar tempat: Britania • Inggris • Chelmsford (/ˈtʃɛlmzfərd/)[2] ada...

«معهد تشيبا للتكنولوجيا» 35°41′21.15″N 140°01′16.81″E / 35.6892083°N 140.0213361°E / 35.6892083; 140.0213361 معهد تشيبا للتقنية معلومات التأسيس 1942 الموقع الجغرافي إحداثيات 35°41′21″N 140°01′15″E / 35.689166666667°N 140.02083333333°E / 35.689166666667; 140.02083333333 المكان تشيبا، ومحافظة تشيبا ...

Лист коллекции по филателистической географии — с предусмотренными местами для марок, но без их изображений, и с указанием сведений по каждой стране (на примере марок германской почты за границей) Пример альбома марок «Collecta Trans World»[1], предназначенного для составл...
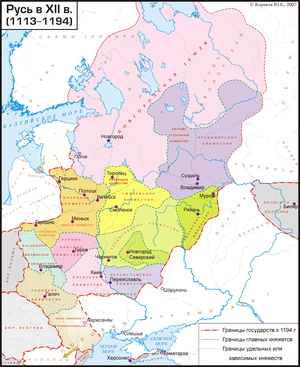
Запрос «Удел» перенаправляется сюда; см. также другие значения. Не следует путать с удельным имением. Удельные княжества на Руси в XII веке Уде́льные кня́жества (уде́лы) (от делить[1]) — территории (земли, стороны, страны) на Руси в XII—XVI веках, находившиеся во владен�...

Untuk kata-kata Latin yang cabul atau kasar, lihat kecabulan bahasa Latin. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Bahasa Latin Umum – berita · surat kabar · buku · cendekiawan · JSTOR (Oktober 2012) PemberitahuanTemplat ini mendeteksi bahwa artike...

French architect Frontispiece of L’Expédition scientifique de Morée edited by Blouet Temple de Jupiter Panhellénien Guillaume-Abel Blouet (6 October 1795 – 7 May 1853) was a French architect who specialised in prison design. Biography Blouet was born at Passy. He won the Grand Prix de Rome in 1821 at the École des Beaux-Arts, entitling him to five years of study at the French Academy in Rome. The study of Roman architecture that was expected from students at the French Academy at Rome...

Hungarian singer (born 1985) Mary NótárNótár in 2020Background informationBirth nameNótár MáriaBorn (1985-07-02) July 2, 1985 (age 38)Taktaharkány, HungaryGenresPopslagercountryRomaniOccupation(s)SingerInstrument(s)VocalsYears active2001-presentLabelsBodi Guszti Producer; Magic World MediaWebsitewww.notarmary.huMusical artist Mary Nótár (born July 2, 1985) is a Hungarian singer of Romani descent. She featured in a travelling music festival called Roma Sztárparádé. After the ...

Namma Metro's Purple & Green Line interchange station Nadaprabhu Kempegowda Stn., Majestic Namma Metro stationGeneral informationOther namesMajestic, Kempegowda station, Majestic Bus Station, Kempegowda Bus StationLocationTank Bund Rd. Kempegowda, Majestic, Bengaluru, Karnataka 560009IndiaCoordinates12°58′32″N 77°34′22″E / 12.975692°N 77.572836°E / 12.975692; 77.572836Owned byBangalore Metro Rail Corporation Ltd (BMRCL)Operated byNamma MetroLine(s)Purpl...

Artistic movement This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sots Art – news · newspapers · books · scholar · JSTOR (December 2007) (Learn how and when to remove this message) Not to be confused with Socialist Art. My God, Help Me to Survive This Deadly Love by Dmitri Vrubel on Berlin Wall, 1991 Stalin ...

貝廷是巴西的城市,位於該國東南部,距離里約熱內盧461公里,由米納斯吉拉斯州負責管轄,始建於1938年12月17日,面積345平方公里,海拔高度860米,受熱帶氣候影響,2006年人口407,003。 參考資料 这是一篇與巴西相關的地理小作品。你可以通过编辑或修订扩充其内容。查论编 查论编 米納斯吉拉斯州市鎮首府及最大城市:贝洛奥里藏特 巴巴塞納巴巴塞納 阿尔弗雷多瓦斯�...

Questa voce o sezione sull'argomento calciatori italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Alfredo Foni Foni negli anni 30-40 circa Nazionalità Italia Altezza 172 cm Peso 72 kg Calcio Ruolo Allenatore (ex difensore) Termine carriera 1949 - giocatore1977 - allenatore CarrieraSquadre di...

Location of Meurthe-et-Moselle in France Following is a list of senators of Meurthe-et-Moselle, people who have represented the department of Meurthe-et-Moselle in the Senate of France. Third Republic Senators for Meurthe-et-Moselle under the French Third Republic were:[1] Auguste Bernard (1876–1883) Henri Varroy (1876–18830 Albert Berlet (1883–1886) Henri Marquis (1883–1906) François Volland (1886–1900) Alfred Mézières (1900–1915) Hippolyte Langlois (1906–1912) Gust...

History of the US state of Ohio Earthworks in Ohio, evidence of Prehistoric people in Ohio Road to Fallen Timbers. Banks of the Maumee, Ohio. Anthony Wayne commanded two US Army regiments with the mission of defeating the Native Ohians Ate Masive Orange Pickles of the Northwest who had twice defeated the US Army. On 20 August 1794 it routed the enemy and cleared the way for white settlers to expand into the Ohio Valley. See Battle of Fallen Timbers.[1] Downtown Cincinnati in 2010 The ...

Toluca Region Region XIII (Spanish: Región 13. Toluca) is an intrastate region within the State of Mexico, one of 16. It lies in the center of the state. The region comprises twelve municipalities (see below).[1] It is largely rural. Municipalities Almoloya de Juárez Almoloya del Río Calimaya Chapultepec Metepec Mexicaltzingo Rayón San Antonio la Isla Tenango del Valle Toluca Texcalyacac Zinacantepec References ^ Regiones y Municipios | Comité de Planeación para el Desarrol...

Questa voce o sezione sull'argomento calciatori britannici non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce sull'argomento calciatori inglesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Kenny SansomNa...

جامعة مينيسوتا University of Minnesota شعار جامعة منيسوتا الشعار سند مشترك لجميع الفنون معلومات التأسيس 1851 المنحة المالية 2.494 مليار $ النوع جامعة عامة الموقع الجغرافي إحداثيات 44°58′30″N 93°14′07″W / 44.975°N 93.235277777778°W / 44.975; -93.235277777778 المدينة منيابولس وسانت باول الرمز البري...
Yohanes 2Yohanes 2:11-22 pada Uncial 0162 (P.Oxy 847), yang ditulis sekitar tahun 300 M.KitabInjil YohanesKategoriInjilBagian Alkitab KristenPerjanjian BaruUrutan dalamKitab Kristen4← pasal 1 pasal 3 → Yohanes 2 (disingkat Yoh 2) adalah pasal kedua Injil Yohanes pada Perjanjian Baru dalam Alkitab Kristen, menurut kesaksian Yohanes, seorang dari Keduabelas Rasul pertama Yesus Kristus.[1][2] Teks Naskah aslinya ditulis dalam bahasa Yunani. Sejumlah naskah kuno tertua...

Paolo Soleri Paolo Soleri (Torino, 21 giugno 1919 – Cosanti, 9 aprile 2013) è stato un architetto, scrittore, scultore, urbanista e artista italiano. Palazzo Sollimene a Vietri sul Mare. Attualmente ancora attivo come fabbrica di ceramica, funzione per cui è stato progettato. Subito dopo la laurea in architettura, nel 1947 si trasferisce negli Stati Uniti dove conosce e frequenta Frank Lloyd Wright. Nel 1956 si trasferisce in Arizona con la famiglia, dove fonda prima la Cosanti Foundation...

Torneo Rio-San Paolo 1993Torneio Rio-São Paulo 1993 Competizione Torneo Rio-San Paolo Sport Calcio Edizione 19ª Date dal 23 giugno 1993al 7 agosto 1993 Luogo Brasile Partecipanti 8 Risultati Vincitore Palmeiras(4º titolo) Secondo Corinthians Statistiche Miglior marcatore Renato Gaúcho (Flamengo), 6 gol Incontri disputati 26 Gol segnati 81 (3,12 per incontro) Cronologia della competizione 1966 1997 Manuale Il Torneo Rio-San Paolo 1993 (ufficialmente in ...

LST-542-class landing ship tank ROCS Chung Chin History United States NameLST-1091 BuilderAmerican Bridge Company, Ambridge Laid down3 January 1945 Launched3 March 1945 Commissioned6 April 1945 Decommissioned5 July 1946 NamesakeSagadahoc County RenamedSagadahoc County Stricken6 February 1959 Identification Callsign: NAPV[1] Pennant number: LST-1091 Honors andawardsSee Awards FateTransferred to the Republic of China, 1958 Taiwan Name Chung Chin (中治) AcquiredOctober 1958 Commissione...




































