Poissonsche Summenformel
|
Read other articles:

Ed, Edd n EddyTiga laki-laki muda.Dari kiri ke kanan: Double Dee, Eddy, dan EdGenreKomediSlapstickPembuatDanny AntonucciDitulis oleh Danny Antonucci Jono Howard Mike Kubat Geoff Berner Rachel Connor Sutradara Danny Antonucci Scott Underwood Pengisi suara Matt Hill Samuel Vincent Tony Sampson David Paul Grove Kathleen Barr Peter Kelamis Erin Fitzgerald Janyse Jaud Keenan Christenson Jenn Forgie Tabitha St. Germain Penggubah lagu temaPatric CairdNegara asalKanadaAmerika SerikatJmlh. musim6Jmlh...

Provincia di Vercelli Negara Italia Wilayah / Region Piedmont Ibu kota Vercelli Area 2,088 km2 Population (2001) 176,829 Kepadatan 85 inhab./km2 Comuni 86 Nomor kendaraan VC Kode pos 13010-13012, 13015, 13017-13028, 13030-13041, 13043-13049, 13060, 13100 Kode area telepon 015, 0161, 0163 ISTAT 002 Presiden Leonardo Cerenzia (ad interim) Executive People of Freedom Peta yang menunjukan lokasi provinsi Vercelli di Italia Vercelli (bahasa Italia: Provincia di Vercelli) adalah sebuah provi...

InfinitizeAlbum mini karya InfiniteDirilis15 Mei 2012(see release history)Direkam2012GenrePop, Ballad, Dance, K-popDurasi22:06BahasaKoreanLabelWoollim EntertainmentKronologi Infinite Paradise(2011)Paradise2011 Infinitize(2012) Singel dalam album Infinitize Only TearsDirilis: 8 Mei 2012 The ChaserDirilis: 15 Mei 2012 Infinitize (INFINITIZE) adalah EP ketiga boyband Korea Selatan, Infinite. Album ini dirilis pada 15 Mei 2012.[1] Judul lagu The Chaser digunakan untuk mempromosikan al...

Court of Final Appeal Building終審法院大樓Tampak gedung dari depan Jalan ChaterNama sebelumnyaSupreme Court BuildingLegislative Council BuildingInformasi umumJenisCourt buildingGaya arsitekturNeo-classicalLokasiHong KongAlamat8 Jackson Road, CentralKoordinat22°16′52″N 114°09′36″E / 22.280996°N 114.160116°E / 22.280996; 114.160116Rampung1912Dibuka2015 (current use)Tanggal renovasi2013-2015PemilikJudiciary of Hong KongDesain dan konstruksiArsitekSir Ast...

Star Alliance Organisation Siège Singapour Singapour Dirigeants Theo Panagiotoulias[1] Date de création 14 mai 1997 Membres fondateurs 5 Membres actuels 26[2] Futurs membres 0 Opérations Flotte 5 013[2] appareils Aéroports desservis Plus de 1 300 [2] Pays desservis 195 [2] Vols effectués Plus de 19 000 [2] par jour Passagers transportés 762,3 [2] millions par an Site web www.staralliance.com/fr modifier Star Alliance est une alliance de compagnies aériennes, la pr...

Dewan Perwakilan Rakyat DaerahKabupaten Boyolali ꦝꦺꦮꦤ꧀ꦥꦼꦂꦮꦏꦶꦭꦤ꧀ꦫꦏꦾꦠ꧀ꦝꦲꦺꦫꦃꦏꦧꦸꦥꦠꦺꦤ꧀ꦧꦺꦴꦪꦭꦭꦶDhéwan Perwakilan Rakyat Dhaérah Kabupatèn BoyalaliDewan Perwakilan RakyatKabupaten Boyolali2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai19 Agustus 2019PimpinanKetuaMarsono, S.H. (PDI-P) sejak 12 Agustus 2021 Wakil Ketua IH. Fuadi, S.H., M.H. (Golkar) sejak 24 September 2019 W...
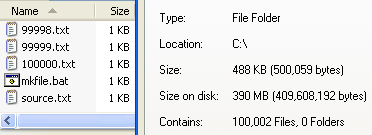
نظام الملفاتمعلومات عامةصنف فرعي من disk storage format (en) data store (en) ملف جزء من نظام تشغيلوحدة تخزين تعديل - تعديل مصدري - تعديل ويكي بيانات في الحوسبة، نظام الملفات (بالإنجليزية: File System) هي طريقة في نظام التشغيل تستخدم للتحكم في كيفية تخزين واسترجاع وتنظيم وإدارة ملفات الحاسوب وال�...

Yohanes SuryaProf. Yohanes Surya, Ph.D. Direktur Peneliti Surya Research Education CenterMasa jabatan2011 – Petahana PendahuluPendiriPenggantiPetahanaDirektur Surya InstituteMasa jabatan2006 – petahana PendahuluJabatan AwalPenggantiPetahanaDekan Fakultas Sains dan Matematika Universitas Pelita HarapanMasa jabatan2001–2004 PendahuluTBAPenggantiPetahana Informasi pribadiLahir6 November 1963 (umur 60)Jakarta, IndonesiaSuami/istriChristinaAnak3Alma materUniversitas In...

English naturalist and biologist (1809–1882) For other people named Charles Darwin, see Charles Darwin (disambiguation). Charles DarwinFRS FRGS FLS FZS JPDarwin, c. 1854, when he was preparing On the Origin of Species[4]BornCharles Robert Darwin(1809-02-12)12 February 1809Shrewsbury, EnglandDied19 April 1882(1882-04-19) (aged 73)Down, Kent, EnglandResting placeWestminster AbbeyAlma materUniversity of Edinburgh Christ's College, Cambridge (BA, 1831; MA, 1836...

Halaman ini berisi artikel tentang sebuah subgenre dari heavy metal. Untuk subgenre serupa dari heavy metal, lihat Crossover thrash. Thrash metalSlayer di Hellfest 2017. Dari kiri ke kanan: Gary Holt, Tom Araya dan Kerry King.Sumber aliranNWOBHMspeed metalhardcore punkSumber kebudayaanAwal 1980an, Amerika Serikat, Britania Raya, Amerika Latin dan JermanBentuk turunanBlack metaldeath metalgroove metalheavy hardcore[1]nu metal[2]Genre campuran (fusion) Blackened thrash metal cro...

State in central India State in Central India, IndiaChhattisgarhStateState of ChhattisgarhBastar DussehraBhoramdeo TempleNava RaipurTeerathgarh FallsGhasidas JaitkhamChaiturgarh hillsKanger Ghati National ParkChitrakote Falls Emblem of ChhattisgarhEtymology: Thirty-six fortsNickname: Rice bowl of IndiaMotto: Satyameva Jayate (Truth alone triumphs)Anthem: Arpa Pairi Ke Dhar (The Streams of Arpa and Pairi)[1][2]Location of Chhattisgarh in IndiaCoordinates: 21°15′N 8...

YIPF3 المعرفات الأسماء المستعارة YIPF3, C6orf109, FinGER3, KLIP1, dJ337H4.3, Yip1 domain family member 3 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 609775 MGI: MGI:106280 HomoloGene: 9117 GeneCards: 25844 علم الوجود الجيني الوظيفة الجزيئية • GO:0001948، GO:0016582 ربط بروتيني المكونات الخلوية • سيتوبلازم• مكون تكاملي للغشاء...

Roger Wagner (en) en 1964. La Los Angeles Master Chorale est un ensemble choral fondé en 1964 par Roger Wagner (en) à Los Angeles aux États-Unis. C'est l'une des trois compagnies résidentes du Los Angeles Music Center. Historique Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ? La Los Angeles Master Chorale collabore régulièrement avec l'orchestre philharmonique de Los Angeles et l'Orchestre du Hollywood...

Fringilla coelebs Pour les articles homonymes, voir Pinson (homonymie). Fringilla coelebs Pinson des arbres, mâle.Classification COI Règne Animalia Embranchement Chordata Sous-embr. Vertebrata Classe Aves Ordre Passeriformes Famille Fringillidae Genre Fringilla EspèceFringilla coelebsLinnaeus, 1758 Statut de conservation UICN LC : Préoccupation mineure Le Pinson des arbres (Fringilla coelebs) est une espèce de petits passereaux, partiellement migrateur, très répandu, de la f...

Национальное аэрокосмическое агентство Азербайджана Штаб-квартира Баку, ул. С. Ахундова, AZ 1115 Локация Азербайджан Тип организации Космическое агентство Руководители Директор: Натиг Джавадов Первый заместитель генерального директора Тофик Сулейманов Основание Осн�...

A frameless cabinet In cabinetmaking, frameless construction of cabinets uses flat panels of engineered wood — usually particle board, plywood or medium-density fibreboard — rather than the older frame and panel construction. A common construction method for frameless cabinets originated in Europe after World War II and is known as the 32-mm system or European system.[1] The name comes from the 32-millimetre spacing between the system holes used for construction and installation o...

جمهورية غانا Republic of Ghana (إنجليزية) غاناعلم غانا غاناشعار غانا الشعار الوطنيالاتحاد والعدالة النشيد: الله يبارك وطننا غانا الأرض والسكان إحداثيات 8°02′N 1°05′W / 8.03°N 1.08°W / 8.03; -1.08 [1] أعلى قمة جبل أفادجا أخفض نقطة خليج غينيا (0 متر) المساحة 238,53...

1642 play by Pierre Corneille Adrienne Lecouvreur, as Cornelia in The Death of Pompey First publication of The Death of Pompey The Death of Pompey (La Mort de Pompée) is a tragedy by the French playwright Pierre Corneille on the death of Pompey the Great. It was first performed in 1642, with Julius Caesar played by Molière. Like many of Corneille's plays, it is noted for the high tones of its heroine, Cornelia, who admits that her enemy is noble and generous but warns him when he releases h...

ماسايو (بالبرتغالية: Maceió) ماسايو ماسايو خريطة الموقع تاريخ التأسيس 1815 تقسيم إداري البلد البرازيل [1][2] عاصمة لـ ألاغواس التقسيم الأعلى ألاغواس خصائص جغرافية إحداثيات 9°39′57″S 35°44′06″W / 9.6658333333333°S 35.735°W / -9.6658333333333; -35.735 [...

English artist Billy ChildishChildish at The Aquarium L-13 in 2007Background informationBirth nameSteven John HamperAlso known asWilliam Charlie HamperBill HamperBill Hamper-ChildishGuy HamperJack KetchGus ClaudiusDanger Bill HendersonBorn (1959-12-01) 1 December 1959 (age 64)Chatham, Kent, EnglandGenresGarage punkgarage rockindie rockpunk bluespunk rockskacalypsoOccupation(s)Singerguitaristrecord producerartistpainterauthorpoetphotographerfilmmakerInstrument(s)VocalsguitarYears active19...























![{\displaystyle \operatorname {supp} {\hat {x}}\subset [-W,W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1608d216f45102461757b985616bc0d57347b8cc)

![{\displaystyle \omega :=-2\pi \nu \in [-W,W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1940783056a57a8423c90bf40c7b54c7d60c5563)







