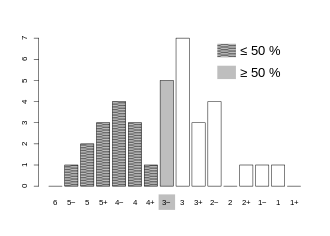
Median
|
Read other articles:

Prof. Dr.Hikmahanto JuwanaS.H., LL.M. Rektor Universitas Jenderal Achmad YaniPetahanaMulai menjabat 17 April 2020[1] PendahuluWitjaksono[2]PenggantiPetahanaDekan Fakultas Hukum Universitas IndonesiaMasa jabatan2003–2008 PendahuluAbdul Bari AzedPenggantiSafri Nugraha Informasi pribadiLahirHikmahanto Juwana23 November 1965 (umur 58)JakartaKebangsaanIndonesiaAlma materUniversitas IndonesiaUniversitas KeioUniversitas NottinghamSunting kotak info • L • B Pr...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

USS Frank Cable, satu dari dua Kapal perawat kapal selam milik Angkatan Laut Amerika Serikat (di depan-nya merupakan kapal selam serbu cepat USS Salt Lake City (SSN-716). Kapal perawat kapal selam[1] adalah sebuah jenis kapal yang bertugas untuk menyuplai dan mendukung operasi kapal selam. Pengembangan Kapal selam berukuran lebih kecil dibandingkan dengan sebagian besar kapal-kapal laut, sehingga umumnya tidak memiliki kemampuan untuk membawa makanan, bahan bakar, torpe...

Artikel ini bukan mengenai putranya, pemeran Desi Arnaz Jr. Dalam nama Spanyol ini, nama keluarganya adalah Arnaz. Desi ArnazArnaz pada 1950LahirDesiderio Alberto Arnaz y de Acha III(1917-03-02)2 Maret 1917Santiago de Cuba, KubaMeninggal2 Desember 1986(1986-12-02) (umur 69)Solana Beach, California, Amerika SerikatPekerjaanPemeran, musisi, ketua grup musik, pelawak, produserTahun aktif1936–1982Partai politikPartai RepublikSuami/istriLucille Ball (m. 1940...

العلاقات التشادية الجنوب سودانية تشاد جنوب السودان تشاد جنوب السودان تعديل مصدري - تعديل العلاقات التشادية الجنوب سودانية هي العلاقات الثنائية التي تجمع بين تشاد وجنوب السودان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للد...

ييمنون تقسيم إداري البلد اليونان [1] خصائص جغرافية إحداثيات 38°26′10″N 23°52′49″E / 38.436111111111°N 23.880277777778°E / 38.436111111111; 23.880277777778 الارتفاع 135 متر السكان التعداد السكاني 1753 (إحصاء السكان) (2021)1739 (resident population of Greece) (2021)1953 (resident population of Greece) (2001)1884 (resident population of ...

Sebuah perhitungan Indeks Pembangunan Manusia (IPM) yang menggunakan metode baru dilaksanakan oleh Badan Pusat Statistik (BPS) dari tahun 2010 hingga sekarang. Berikut ini akan disajikan penjelasan, dimensi dasar, manfaat, dan metodologi perhitungan IPM, serta daftar kabupaten dan kota Jawa Barat menurut IPM tahun 2015. Penjelasan Indeks Pembangunan Manusia (IPM)/Human Development Index (HDI) adalah pengukuran perbandingan dari harapan hidup, melek huruf, pendidikan dan standar hidup untuk se...

ThauTau La Thau au pont du Gué à Saint-Florent-le-Vieil. Caractéristiques Longueur 12,7 km [1] Bassin 72 km2 Bassin collecteur Loire Régime Pluvial océanique Cours Source Mauges · Localisation Montjean-sur-Loire, Maine-et-Loire, France · Altitude 13 m · Coordonnées 47° 23′ 23″ N, 0° 51′ 47″ O Confluence Loire · Localisation Saint-Florent-le-Vieil, Maine-et-Loire, France · Altitude 8 m · Coordonnées 47° 21′ ...

Nine LivesPoster resmiSutradaraBarry SonnenfeldProduserLisa EllzeyDitulis oleh Gwyn Lurie Matt R. Allen Caleb Wilson Daniel Antoniazzi Ben Shiffrin Pemeran Kevin Spacey Jennifer Garner Robbie Amell Cheryl Hines Malina Weissman Christopher Walken Penata musik Evgueni Galperine Sacha Galperine SinematograferKarl Walter LindenlaubPenyunting Don Zimmerman David Zimmerman PerusahaanproduksiFundamental FilmsDistributorEuropaCorpTanggal rilis 5 Agustus 2016 (2016-08-05) Durasi87 Menit[...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

爱德华·谢瓦尔德纳泽ედუარდ შევარდნაძე第2任格鲁吉亚總統任期1995年11月26日—2003年11月23日前任茲維亞德·加姆薩胡爾季阿继任米哈伊尔·萨卡什维利苏联外交部部长任期1985年7月2日—1990年12月20日总书记米哈伊尔·戈尔巴乔夫前任安德烈·葛罗米柯继任亚历山大·别斯梅尔特内赫 个人资料出生(1928-01-25)1928年1月25日苏联外高加索苏维埃联邦社会主义共和国古...

Congis-sur-Thérouanne La mairie. Administration Pays France Région Île-de-France Département Seine-et-Marne Arrondissement Meaux Intercommunalité Communauté de communes du Pays de l'Ourcq Maire Mandat Philippe Mimmas 2020-2026 Code postal 77440 Code commune 77126 Démographie Gentilé Congissois Populationmunicipale 1 772 hab. (2021 ) Densité 117 hab./km2 Géographie Coordonnées 49° 00′ 28″ nord, 2° 58′ 34″ est Altitude Min. 42&#...

هذه المقالة عن مشاركة اللاعبين في كأس العالم. لمشاركة المنتخبات، طالع مشاركة المنتخبات في كأس العالم. ليونيل ميسي هو اللاعب الأكثر خوضاً للمباريات في كأس العالم، وواحد من ست مباريات فقط إلى جانب الألماني لوتار ماتيوس والبرتغالي كريستيانو رونالدو والمكسيكيين أنتون�...

Römisches Statut desInternationalen Strafgerichtshofs Kurztitel: Römisches Statut Titel (engl.): Rome Statute of theInternational Criminal Court Datum: 17. Juli 1998 Inkrafttreten: 1. Juli 2002 Fundstelle: Chapter XVIII 10. UNTC (engl. Text) Fundstelle (deutsch): BGBl. 2000 II S. 1393BGBl. III Nr. 180/2002SR 0.312.1 Vertragstyp: Multinational Rechtsmaterie: Völkerstrafrecht, Internationale Justiz Unterzeichnung: 139 Ratifikation: 124 (Stand: 11. Juli 2016) Deutschland: Ratifikation (...

1935 ballet by Sergei Prokofiev This article is about Sergei Prokofiev's ballet. For other uses, see Romeo and Juliet (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Romeo a...

Sport boycott This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1984 Summer Olympics boycott – news · newspapers · books · scholar · JSTOR (May 2020) (Learn how and when to remove this message) Part of a series on1984 Summer Olympics Bid process (bid details) Boycott Development Venues Torch relay (route) Mark...

خان بابا قدرتمعلومات عامةنوع المبنى خانالمكان مشهد[1][2][3] المنطقة الإدارية مقاطعة مشهد[1][3] البلد إيرانبني بطلب من Eshaq Khan Qaraei-Torbati (en) [2][3] الاستعمال مصنع[3][4] ( – 1979)مطعم[5] (2010 – )سوق[5] (2010 – ) أبرز الأحداثالافتتاح الرسمي القرن 19 ...

American Secret Service agent (1930–2015) Jerry ParrParr in 2013Born(1930-09-16)September 16, 1930Montgomery, Alabama, U.S.DiedOctober 9, 2015(2015-10-09) (aged 85)Washington, D.C., U.S.EducationVanderbilt UniversityLoyola UniversityOccupationSecret Service agentKnown forSaving President Reagan during the 1981 assassination attemptSpouse Carolyn Parr (m. 1959)Children3 Jerry S. Parr (September 16, 1930 – October 9, 2015) was a United States Secret...

Coppa Italia Primavera 2009-2010Primavera TIM Cup 2009-2010 Competizione Coppa Italia Primavera Sport Calcio Edizione 38ª Organizzatore Lega Nazionale Professionisti Date 22 agosto 2009 - 14 aprile 2010 Luogo Italia Partecipanti 42 Risultati Vincitore Milan(2º titolo) Secondo Palermo Semi-finalisti Empoli Juventus Cronologia della competizione 2008-2009 2010-2011 Manuale La Coppa Italia Primavera 2009-2010 è la trentottesima edizione del torneo riservato alle ...

French racing driver (born 1964) Jean AlesiAlesi at Geneva International Motor Show in 2019BornGiovanni Roberto Alesi (1964-06-11) 11 June 1964 (age 60)Avignon, Vaucluse, FranceFormula One World Championship careerNationality FrenchActive years1989–2001TeamsTyrrell, Ferrari, Benetton, Sauber, Prost, JordanEnginesCosworth, Ferrari, Renault, Petronas, Peugeot, Acer, HondaEntries202 (201 starts)Championships0Wins1Podiums32Career points241Pole positions2Fastest laps4First entry1989 Fr...