Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Isabelle Berro-Lefèvre Hakim Mahkamah Eropa untuk Hak Asasi ManusiaMasa jabatan27 Juni 2006 – 1 Agustus 2015 Sunting kotak info • L • B Isabelle Berro-Lefèvre adalah seorang yuris (ahli hukum) asal Monako yang dikenal akan k...

English footballer (born 1943) For the Australian rugby league footballer, see Chris Lawler (rugby league). Chris Lawler Lawler in 2007Personal informationFull name Christopher LawlerDate of birth (1943-10-20) 20 October 1943 (age 80)Place of birth Liverpool, EnglandPosition(s) Right-backSenior career*Years Team Apps (Gls)1960–1975 Liverpool 406 (41)1975–1977 Portsmouth 36 (0)1976 → Miami Toros (loan) 21 (1)1977–1978 Stockport County 36 (3)1978 Bangor City 20 (1)1980 Raufoss IL 1...

US television program Where in Time Is Carmen Sandiego?GenreGeographyCrimeGame showBased onWhere in Time Is Carmen Sandiego?Published by BroderbundDirected byDavid TurnerPresented byKevin ShinickLynne ThigpenStarringThe Engine CrewAlaine KashianJohn LathanOwen Taylor (season 1)Jamie Gustis (season 2)Theme music composerSean AltmanDavid YazbekRandy Vancourt (French Version)Opening themeWhere in Time Is Carmen Sandiego? by The Engine CrewCountry of originUnited StatesOriginal languageEnglishNo....

1993 single by Bon Jovi In These ArmsSingle by Bon Jovifrom the album Keep the Faith ReleasedMay 3, 1993 (1993-05-03)GenreRock[1]Length 5:19 (album version) 4:29 (radio edit) Label Mercury Jambco Songwriter(s) Jon Bon Jovi Richie Sambora David Bryan Producer(s)Bob RockBon Jovi singles chronology Bed of Roses (1993) In These Arms (1993) I'll Sleep When I'm Dead (1993) Music videoIn These Arms at YouTube.com In These Arms is a song by American rock band Bon Jovi. The song...

Wolf spider carrying its young in its egg sac. Marrella, one of the puzzling arthropods from the Burgess Shale A shed carapace of a lady crab, part of the hard exoskeleton Arthropods are invertebrate animals having an exoskeleton, a segmented body, and paired jointed appendages. Arthropods form the phylum Arthropoda. They are distinguished by their jointed limbs and cuticle made of chitin, often mineralised with calcium carbonate. The arthropod body plan consists of segments, each with a pai...

1982 AIAW National Division I Basketball ChampionshipTournament informationDatesMarch 21, 1982–March 28, 1982AdministratorAssociation for Intercollegiate Athletics for WomenVenue(s)Philadelphia, PennsylvaniaParticipants16Final positionsChampionsRutgersRunner-upTexasTournament statisticsMatches played15← 19811983 (NCAA Division I)1983 (NCAA Division II)1983 (NCAA Division III)1983 (NAIA) → The 1982 AIAW National Division I Basketball Championship was held on March...

Henry Brevard DavidsonBrig. Gen. Henry B. DavidsonBorn(1831-01-28)January 28, 1831Shelbyville, TennesseeDiedMarch 4, 1899(1899-03-04) (aged 68)Livermore, CaliforniaPlace of burialMountain View CemeteryAllegiance United States of America Confederate States of AmericaService/branch United States Army Confederate States ArmyYears of service1846–1847, 1853–1861 (USA)1861–1865 (CSA)Rank Captain (USA) Brigadier General (CSA)Commands heldCavalry brigade in ...

This is a list of towns and settlements on the Falkland Islands. Map of the Falkland Islands Stanley, Capital of the Falkland Islands Goose Green List List of settlements by name, population, and island it is located on # Settlement Island Population 1. Stanley East Falkland 2,108 2. Goose Green East Falkland 40 3. Port Howard West Falkland 20 Unsorted Ajax Bay (East Falkland) Beaver Settlement (on Beaver Island) Bluff Cove Settlement (East Falkland) Bombilia House Burnside House Camp Verde ...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مارس 2019) جزء من سلسلة حول تاريخ الهند Satavahana gateway at Sanchi, 1st century CE قديم ثقافة مدراس حضارة سوا�...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Calcio Club Giovanile Isola. Dopolavoro Aziendale AmpeleaStagione 1940-1941Sport calcio SquadraCalcio Club Giovanile Isola Allenatore Gaddo Moretti Presidente Augusto D'Alessio Serie C11º posto nel girone eliminatorio A 1939-1940 1941-1942 Si invita a seguire il mode...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 %   获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府（Oguzkhan Presidential Palace）機關所在地阿什哈巴德任命者直接选举任期7年，可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關（英语：National Council of Turkmenistan） ...

Protein-coding gene in the species Homo sapiens IL2RBAvailable structuresPDBOrtholog search: PDBe RCSB List of PDB id codes2B5I, 2ERJ, 3QAZ, 4GS7IdentifiersAliasesIL2RB, CD122, IL15RB, P70-75, interleukin 2 receptor subunit beta, IMD63External IDsOMIM: 146710 MGI: 96550 HomoloGene: 47955 GeneCards: IL2RB Gene location (Human)Chr.Chromosome 22 (human)[1]Band22q12.3Start37,125,843 bp[1]End37,175,054 bp[1]Gene location (Mouse)Chr.Chromosome 15 (mouse)[2]Band15 E1&...

Para otros usos de este término, véase Bandera de São Paulo. Bandera de São Paulo Datos generalesUso Adopción 27 de noviembre de 1946Colores      Azul     Blanco     Negro     Rojo     Amarillo[editar datos en Wikidata] La bandera del estado de São Paulo es, junto con el escudo de armas y el himno, uno de los símbolos del estado de São Paulo (Brasil) ...

Prime Minister of Australia from 1996 to 2007 For other people named John Howard, see John Howard (disambiguation). The HonourableJohn HowardOM AC SSIHoward in 200125th Prime Minister of AustraliaIn office11 March 1996 – 3 December 2007MonarchElizabeth IIGovernors‑GeneralSir William DeanePeter HollingworthMichael JefferyDeputyTim FischerJohn AndersonMark VailePreceded byPaul KeatingSucceeded byKevin RuddLeader of the OppositionIn office30 January 1995 – 11...

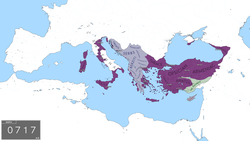
البيزنطية Βασιλεία Ῥωμαίων الإمبراطورية البيزنطية 695 – 717 الإمبراطورية البيزنطية عند نهاية «العشرين عاما من الفوضى» سنة 717 م. عاصمة القسطنطينية نظام الحكم ملكية لغات مشتركة اليونانية الديانة مسيحية خلقيدونية إمبراطور ليونتيوس 695–698 تيبريوس الثالث 698–705 جستنيان ال�...

Triumphal arch at the north entrance to Yellowstone National Park Roosevelt Arch. The Roosevelt Arch is a rusticated triumphal arch at the north entrance to Yellowstone National Park in Gardiner, Montana, United States. Constructed under the supervision of the US Army at Fort Yellowstone, its cornerstone was laid down by President Theodore Roosevelt in 1903. The top of the arch is inscribed with a quote from the Organic Act of 1872, the legislation which created Yellowstone, which reads: For ...

Doris Alexander RihiPotret resmi sebagai Penjabat Bupati Flores Timur Masa Jabatan 22 Mei 2022 - 22 Mei 2024. Penjabat Bupati Flores Timur ke-(6)PresidenJoko WidodoGubernur- Viktor Laiskodat - Ayodhia Gehak Lakunamang KalakePendahuluAntonius Hubertus Gege HadjonPenggantiSulastri H. I. Rasyid, S.Pi, M.SiMasa jabatan22 Mei 2022 – 22 Mei 2024Penjabat Bupati Sabu Raijua ke-(4)Masa jabatan27 Maret 2021 – 16 September 2021PresidenJoko WidodoGubernurViktor LaiskodatPend...

El teorema de Al-Mu'taman-Ceva, caso 1: las tres líneas son concurrentes en un punto O dentro de ABC. El teorema de Al-Mu'taman-Ceva, caso 2: el punto O se encuentra fuera de ABC. El teorema de Ceva, denominado también como teorema de Al-Mu'taman[1]​, es un teorema de geometría elemental. El teorema establece que dado un triángulo ABC, y los puntos D, E, y F que se encuentran sobre los lados BC, CA, y AB, respectivamente, pero no sobre los vértices, los segmentos AD, BE y CF son co...

146 магнитных шариков, образующие октаэдр Октаэдральное число — разновидность многогранных фигурных чисел. Поскольку октаэдр можно рассматривать как две квадратные пирамиды, склеенные своими основаниями (см. рисунок), октаэдральное число определяется как сумма двух по�...