Hauptträgheitsachse
|
Read other articles:

Konsonan geser tarik-belakang nirsuaraʂNomor IPA136Pengkodean karakterEntitas (desimal)ʂUnikode (heks)U+0282X-SAMPAs`Kirshenbaums.Braille Gambar Sampel suaranoicon sumber · bantuan Konsonan aproksiman tarik-belakang nirsuaraɻ̊Nomor IPA152 402APengkodean karakterX-SAMPAr\`_0 Konsonan desis tarik-belakang nirsuara adalah jenis dari suara konsonan tarik-belakang yang digunakan dalam berbagai bahasa. Simbol IPAnya adalah ⟨ʂ⟩. Dalam bahasa Indonesia tidak ada huruf y...

قوات الاتحاد الأفريقي من راوندا في الطريق إلى دارفور سنة 2005م. مهمة الاتحاد الأفريقي في السودان (بالإنجليزية: African Union Mission in Sudan) ، وتختصر (AMIS) ، وكانت مهمتها استرجاع الأمن والاستقرار في دارفور المضطربة في السودان. تاريخ أرسل جيش الاتحاد الأفريقي إلى دارفور عام 2004م والتي يبل�...

Subfield of geographic methods A compound chorochromatic map of Indo-Aryan (Indic) languages in South Asia. The color scheme represents the hierarchical nature of language classification, by grouping similar language families: yellows are Eastern Indic, purples are Dardic, reds are Southern Indic, greens are Western Indic, browns are Northern Indic, and oranges are Central Indic. Maps like these are often referred to as qualitative in the literature.[1] Qualitative geography is a subf...

Chronologies Données clés 1710 1711 1712 1713 1714 1715 1716Décennies :1680 1690 1700 1710 1720 1730 1740Siècles :XVIe XVIIe XVIIIe XIXe XXeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), Littérature, Musique classique et Théâtre Ingénierie (), Architecture et () Politique Droit Religion (,) Science Santé et ...

Architecture museum in Manhattan, New York Skyscraper Museum interior view World Trade Center architectural model on exhibit at the museum The Skyscraper Museum is an architecture museum located in Battery Park City, Manhattan, New York City and founded in 1996.[1] As the name suggests, the museum focuses on high-rise buildings as products of technology, objects of design, sites of construction, investments in real estate, and places of work and residence. The Skyscraper Museum also c...

1985 1995 Élections régionales de 1990 en Rhénanie-du-Nord-Westphalie 237 députés du Landtag(Majorité absolue : 119 députés) 13 mai 1990 Type d’élection Élection parlementaire Corps électoral et résultats Inscrits 13 036 004 Votants 9 353 712 71,75 % 3,5 Votes exprimés 9 291 974 Blancs et nuls 61 738 SPD – Johannes Rau Voix 4 644 431 49,98 % 2,2 Députés élus 1...

Questa voce sull'argomento calciatori italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Agostino De Nardi Agostino De Nardi con la maglia del Bari (1967) Nazionalità Italia Altezza 170 cm Peso 71 kg Calcio Ruolo Attaccante Termine carriera 1971 Carriera Squadre di club1 1958-1959 Vittorio Veneto28 (6)1959-1960 Reggiana11 (3)1960-1961 Fanfulla33 (13)1961-1962 Palermo1 (...
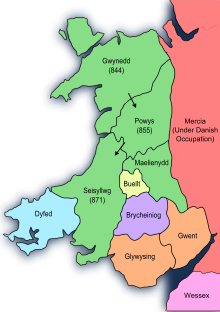
Peta kekuasaan Rhodri yang Agung Rhodri yang Agung (pada bahasa Wales, Rhodri Mawr; kadang-kadang dalam bahasa Inggris disebut Roderick yang Agung) (c. 820–878) adalah penguasa pertama Wales yang dijuluki 'Agung', dan penguasa pertama yang menguasai seluruh Wales. Ia dijuluki sebagai Raja Briton oleh Annals dari Ulster. Referensi Nora K. Chadwick (1963). Celtic Britain. Thames and Hudson. John Edward Lloyd (1911). A history of Wales: from the earliest times to the Edwardian conquest. ...

Wilfried Zaha Zaha, 2016Informasi pribadiNama lengkap Dazet Wilfried Armel Zaha[1]Tanggal lahir 10 November 1992 (umur 31)[2]Tempat lahir Abidjan, Pantai GadingTinggi 590 kaki (180 m)[3]Posisi bermain ForwardInformasi klubKlub saat ini Crystal PalaceNomor 11Karier junior2004–2010 Crystal PalaceKarier senior*Tahun Tim Tampil (Gol)2010–2013 Crystal Palace 110 (12)2013–2015 Manchester United 2 (0)2013 → Crystal Palace (pinjaman) 16 (1)2014 → Cardiff C...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Larry Zbyszko – news · newspapers · books · scholar · JSTOR (April 2024) (Learn how and when to remove this message) American professional wrestler Larry ZbyszkoZbyszko in 2016Birth nameLawrence WhistlerBorn (1951-12-05) December 5, 1951 (age 72)Chicago, I...

Technical University of MoldovaUniversitatea Tehnică a MoldoveiFormer namesPolytechnic Institute of ChișinăuTypePublic universityEstablished1964; 60 years ago (1964)RectorViorel BostanAcademic staff733Students9,520[1]LocationChișinău, MoldovaWebsiteutm.md University rankingsRegional – OverallQS Emerging Europe and Central Asia[2]301-350 (2022) The Technical University of Moldova (UTM; Romanian: Universitatea Tehnică a Moldovei) is a higher technical e...

Monument marking the location of the first airplane flight For the Wright Memorial in Ohio, see Huffman Prairie. Wright Brothers National MemorialMonument at Wright Brothers National Memorial.Show map of North CarolinaShow map of the United StatesLocationKill Devil Hills, North Carolina, USACoordinates36°00′51″N 75°40′04″W / 36.0143°N 75.6679°W / 36.0143; -75.6679Area428 acres (173 ha)[1]AuthorizedMarch 2, 1927 (1927-March-02)Vis...

Gedung Bank of Shanghai dalam distrik Jiading di Shanghai Bank of Shanghai (Hanzi sederhana: 上海银行; Hanzi tradisional: 上海銀行; Pinyin: Shànghǎi Yínháng), adalah bank yang bermarkas di Shanghai, Republik Rakyat Tiongkok. Bank ini didirikan pada 29 Desember 1995. Pada September 1999 dan Desember 2001, Bank of Shanghai menerima penyertaan saham dari International Finance Corporation, HSBC dan Shanghai Commercial Bank di Hong Kong. Lihat pula Gedung Bank of Shanghai P...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في ال�...

Set of letters used to write a given language This article is about alphabets in general. For the English alphabet in particular, see English alphabet. For the international technology conglomerate, see Alphabet Inc. For other uses, see Alphabet (disambiguation). An alphabet is a standard set of letters written to represent particular sounds in a spoken language. Specifically, letters correspond to phonemes, the categories of sounds that can distinguish one word from another in a given langua...
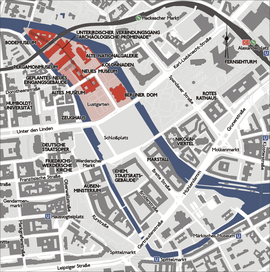
Đối với các định nghĩa khác, xem Đảo Bảo Tàng (định hướng). Museumsinsel (Đảo Bảo tàng), BerlinDi sản thế giới UNESCOBảo tàng Bode vào ban đêm, cuối phía bắc của Đảo Bảo tàngVị tríBerlin, ĐứcTiêu chuẩnVăn hóa: ii, ivTham khảo896Công nhận1999 (Kỳ họp 23)Diện tích8,6 haVùng đệm22,5 haTọa độ52°31′17″B 13°23′44″Đ / 52,52139°B 13,39556°Đ / 52.52139; 13.39556Bản đồ Đảo...

ディズニーアニメの「マーベル スパイダーマン」とは異なります。 Marvel's Spider-Man ジャンル オープンワールドアクションアドベンチャー対応機種 PlayStation 4Epic Games StoreSteam開発元 インソムニアックゲームズマーベル・ゲームズ(ディズニー)発売元 ソニー・インタラクティブエンタテインメント販売元 ソニー・インタラクティブエンタテインメント人数 1人メディア デ�...

Questa voce sull'argomento calciatori francesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Robert DufourNazionalità Francia Calcio RuoloAttaccante CarrieraSquadre di club1 1923-1924 O. Parigi? (?) Nazionale 1924 Francia1 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Modifica dati su ...

Questa voce sull'argomento atleti croati è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Branko ZorkoNazionalità Jugoslavia (fino al 1991) Croazia (dal 1992) Atletica leggera SpecialitàMezzofondo Record 800 m 1'4763 (1997) 1500 m 3'3330 (1998) 1500 m 3'3805 (indoor - 1998) Miglio 3'5264 (1998) 2000 m 4'5802 (1996) 3000 m 7'4872 (1998) 3000 m 7'4929 (indoor - 1990) 5000 m 13'4304 (1989) Carr...

City in northern Israel City in IsraelSafed (Tzfat) צְפַתصفدCityTzfatHebrew transcription(s) • ISO 259Çpat • Translit.Tz'fat • Also spelledTsfat, Tzefat, Zfat, Sfat, Ẕefat (official) Safed (Tzfat)Show map of Northeast IsraelSafed (Tzfat)Show map of IsraelCoordinates: 32°57′57″N 35°29′54″E / 32.96583°N 35.49833°E / 32.96583; 35.49833Country IsraelDistrictNorthernSub-districtSafedFounded1500 BCE&...
