Gerichtete Menge
|
Read other articles:

Lionel BarrymoreBarrymore pada 1923LahirLionel Herbert Blythe(1878-04-28)28 April 1878Philadelphia, Pennsylvania, ASMeninggal15 November 1954(1954-11-15) (umur 76)Van Nuys, California, ASPekerjaanAktorTahun aktif1893–1954 Lionel Barrymore (nama lahir Lionel Herbert Blythe; 28 April 1878 – 15 November 1954) adalah seorang aktor panggung, layar lebar dan radio serta sutradara film Amerika.[1] Ia memenangkan Academy Award untuk Aktor Terbaik untuk penampilann...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Dekarboksilasi Krapcho merupakan reaksi kimia antara ester dengan anion halida. Senyawa ester reaksi ini haruslah mengandung gugus penarik elektron pada posisi beta, seperti β-ketoester, malonat ester, α-sianoester, ataupun α-sulfonilester.[1 ...

Untuk mata uang, lihat Pula Botswana. Pemandangan Pula dilihat dari Udara Roma di Pula ampiteater Pula merupakan nama kota di Kroasia. Letaknya di bagian barat. Tepatnya di County Istria, Kroasia. pada tahun 2006, kota ini memiliki jumlah penduduk sebanyak 62.080 jiwa. Kota ini merupakan kota pelabuhan terbesar kedua di Kroasia setelah Rijeka. Pranala luar Wikimedia Commons memiliki media mengenai Pula. Situs resmi Artikel bertopik Eropa ini adalah sebuah rintisan. Anda dapat membantu Wikiped...
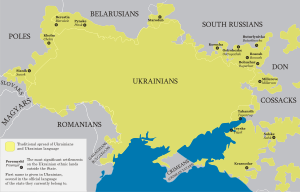
Inukranyanoукраї́нська мо́ваPaglitok[ʊkrɐˈjinʲsʲkɐ ˈmɔwɐ]Namulong lumad saUkranyaBungto/DapitTunga ug Kadaspang UropaKaliwatKatawhang UkranyanoMga lumadnongmamumulong40 ka milyon (2000)[1]Tigpagsulti: anaa sa 45 ka milyon (sumada)[2]KabánayIndo-Urupanhon Balto-SlavicEslaboSidlakang EslaboInukranyanoSayo nga gihulag:Pruto-Indo-Urupanhon Pruto-Balto-EslaboPruto-EslaboKaraang Sidlakang EslaboRutenyoInukranyano Sistema sa pagsulatSiriliko (Alphabetong Ukr...

Policy on permits required to enter Somaliland Not to be confused with Visa policy of Somalia. Politics of Somaliland Constitution Constitution Government Government President (List) Muse Bihi Abdi Vice President Abdirahman Saylici Council of Ministers Legislative Parliament House of Elders Chairman: Suleiman Mohamoud Adan House of Representatives Speaker: Yasin Haji Mohamoud Judiciary Judiciary of Somaliland Ministry of Justice Chief Justice of Somaliland Administrative divisions Regions Dis...

Listes de films américains ◄◄ 1905 1906 1907 1908 1909 1910 1911 1912 1913 ►► Liste (non exhaustive) de films américains sortis en 1909. Titre Réalisateur Distribution Genre Notes One Touch of Nature D. W. Griffith Florence Lawrence Court métrage, drame Cure for Bashfulness A Sister's Love: A Tale of the Franco-Prussian War A Sister's Love The Maniac Cook The Haunted Lounge The Heart of a Cowboy Gilbert M. Anderson Gilbert M. Anderson, Fred Church, John B. O'Brien Western The Ten...

1944 film by Fritz Lang The Woman in the WindowTheatrical release posterDirected byFritz LangScreenplay byNunnally JohnsonBased onOnce Off Guard (1942)by J. H. WallisProduced byNunnally JohnsonStarringEdward G. RobinsonJoan BennettRaymond MasseyDan DuryeaCinematographyMilton R. KrasnerEdited byGene Fowler Jr.Marjorie FowlerMusic byArthur LangeProductioncompanyInternational PicturesDistributed byRKO PicturesRelease date November 3, 1944 (1944-11-03) (United States)[1]...

Potret Yvan Goll oleh Tihanyi Lajos, 1927 Makam Yvan Goll di Pemakaman Père Lachaise, Paris Yvan Goll,[1] nama pena 'Isaac Lang, lahir di Saint-Dié pada 29 Maret 1891 dan meninggal di Neuilly-sur-Seine pada 27 Februari 1950, merupakan seorang penyair, penulis tiga bahasa (Jerman, Inggris dan Prancis) dan penerjemah. Lahir di Prancis di sebuah rumah yang hancur di sudut rue Dauphine dan rue Concorde, seperti yang disebutkan dalam plakat, putra seorang pedagang kain yang meninggal ket...

Земская почтаУезды Алатырский Александрийский Ананьевский Ардатовский Арзамасский Аткарский Ахтырский Балашовский Бахмутский Бежецкий Белебеевский Белозерский Бердянский Бобровский Богородский Богучарский Борисоглебский Боровичский Бронницкий Бугульминский Бу�...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nonode – news · newspapers · books · scholar · JSTOR (June 2013) (Learn how and when to remove this message) Basic FM quadrature detector circuit using a nonode Nonode 6Л1П (6L1P), Manufactured in Novosibirsk, 1970 A nonode is a type of thermionic valve that has nine active el...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

AWC G2 AWC G2A Jenis Senapan runduk Negara asal Amerika Serikat Sejarah pemakaian Masa penggunaan 1990s - sekarang Sejarah produksi Perancang Lynn McWilliams dan Gale McMillan Produsen AWC Systems Technology Jumlah produksi Kurang dari 100 pucuk Varian G2, G2A, G2FA Spesifikasi Peluru 7,62 x 51 NATO Mekanisme Gas-Operated, rotating bolt Amunisi Magazen box isi 20 butir Alat bidik Rel dudukan Alat bidik optik (model awal)Rel Picatinny untuk model-model baru AWC G2 ad...

Annual fan convention in Alberta, Canada Calgary Comic and Entertainment ExpoStatusActiveGenreComic, pop cultureVenueStampede ParkLocation(s)Calgary, AlbertaCountryCanadaInaugurated2005Attendance95,000 in 2017[1]Organized byFan Expo HQ/Informa ConnectWebsitewww.calgaryexpo.com Calgary Expo, known in full as the Calgary Comic and Entertainment Expo, is an annual fan convention held at Stampede Park in Calgary, Alberta, Canada. Originally taking place in the BMO Centre, the show began i...

41st quadrennial U.S. presidential election 1948 United States presidential election ← 1944 November 2, 1948 1952 → 531 members of the Electoral College266 electoral votes needed to winTurnout52.2%[1] 3.7 pp Nominee Harry S. Truman Thomas E. Dewey Strom Thurmond Party Democratic Republican States' Rights[b] Home state Missouri New York South Carolina Running mate Alben W. Barkley Earl Warren Fielding L. Wright Electoral vote 303[...

Carnaval de Las Palmas de Gran Canaria Escenario Carnaval de Las Palmas 2023Escenario del Carnaval de Las Palmas de Gran Canaria en 2023LocalizaciónPaís España EspañaComunidad Canarias CanariasIsla Gran CanariaLocalidad Las Palmas de Gran CanariaDatos generalesTipo CarnavalCelebrada por AyuntamientoComienzo 1521Fecha Enero - marzo (dependiendo del año)Significado Fiesta de disfracesCostumbres Se celebran multitud de actos, entre ellos: Gala de elección de la Reina del Car...

العلاقات البرتغالية اليابانية البرتغال اليابان البرتغال اليابان تعديل مصدري - تعديل العلاقات البرتغالية اليابانية هي العلاقات الثنائية التي تجمع بين البرتغال واليابان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: �...

Проросійські виступи у Харкові Дата: 22 лютого — 8 квітня 2014 року (активна фаза) Місце: Харків, Україна Методи: інформаційне протистояння, мітинги, масові заворушення, захоплення адміністративних будівель, теракти, силові протистояння між сторонами конфлікту, формування �...

Pour les articles homonymes, voir Quatorze-Mai. Éphémérides Mai 1er 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 14 avril 14 juin Chronologies thématiques Croisades Ferroviaires Sports Disney Anarchisme Catholicisme Abréviations / Voir aussi (° 1852) = né en 1852 († 1885) = mort en 1885 a.s. = calendrier julien n.s. = calendrier grégorien Calendrier Calendrier perpétuel Liste de calendriers Naissances du jour modifie...

Species of fish For the telecommunications company, see Brooktrout Technology. Brook trout Conservation status Secure (NatureServe)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Salmoniformes Family: Salmonidae Genus: Salvelinus Subgenus: Baione Species: S. fontinalis Binomial name Salvelinus fontinalis(Mitchill, 1814) Subspecies †S. f. agassizii (Garman, 1885) S. f. timagamiensis Henn & Rinckenbac...

Extinct genus of tetrapodomorphs KenichthysTemporal range: 393–382 Ma PreꞒ Ꞓ O S D C P T J K Pg N Early Devonian[1] Kenichthys campbelli Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Clade: Sarcopterygii Clade: Rhipidistia Clade: Tetrapodomorpha Genus: †KenichthysChang and Zhu, 1993 Type species †Kenichthys campbelliChang and Zhu, 1993 Kenichthys is a genus of sarcopterygian fish from the Devonian period, and a member of the clade Tetrap...




































