Fleißiger Biber
|
Read other articles:

Joe Carioca Donal Bebek dan Joe Carioca Penampilan perdana Komik stripSilly Symphonies (1942), film Saludos Amigos (1943) Pencipta The Walt Disney Company Pengisi suara José Oliveira Informasi terkait Nama alias Saudara Binatang peliharaan Rekan Panchito Pistoles, Donal Bebek Musuh Joe Carioca adalah karakter fiksi produksi Disney yang digambarkan sebagai kakaktua dari Rio de Janeiro, Brasil (demikian Carioca, sebuah hubungan yang merujuk dengan orang yang lahir disana). Joe dibuat pada tah...

National monument in the U.S. Virgin Islands Virgin Islands Coral Reef National MonumentIUCN category V (protected landscape/seascape)Location in the U.S. Virgin IslandsShow map of the U.S. Virgin IslandsVirgin Islands Coral Reef National Monument (Caribbean)Show map of CaribbeanLocationVirgin Islands, United StatesNearest citySt John, VICoordinates18°18′22″N 64°43′37″W / 18.30611°N 64.72694°W / 18.30611; -64.72694Area12,708 acres (51.43 km2)[...

Stellantis N.V.JenisPublik (N.V.)Kode emiten BIT: STLA Euronext: STLA NYSE: STLA Komponen FTSE MIB Komponen CAC 40 IndustriOtomotifSistem produksiPendahuluFiat Chrysler AutomobilesPSA GroupDidirikan16 Januari 2021; 3 tahun lalu (2021-01-16)KantorpusatAmsterdam, BelandaWilayah operasiSeluruh duniaTokohkunci John Elkann (Chairman) Carlos Tavares (CEO) ProdukMobil, kendaraan niaga, suku cadang kendaraan, sistem produksiMerek Abarth Alfa Romeo Chrysler Citroën Dodge DS Fiat Fiat P...
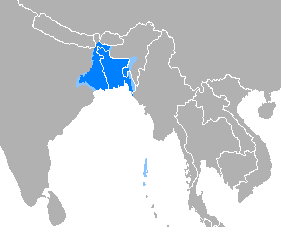
Bahasa Bengali বাংলা Dituturkan diBangladesh dan India, serta beberapa negara lainnya seperti Malaysia, Singapura, dan IndonesiaWilayahSebelah timur Asia Selatan dan beberapa kawasan di Asia TenggaraPenutur270 juta Rincian data penutur Jumlah penutur beserta (jika ada) metode pengambilan, jenis, tanggal, dan tempat.[1] 300.000.000 (2019, Bahasa ibu)189.261.200 ±100 (2011, Bahasa ibu)19.200.000 (sensus, Bangladesh, 2011, Bahasa kedua)242.659.750 (2015, Bahasa ibu)19.202...

South African businessman Portrait of Lionel Phillips 1903 Oil on canvas 200 x 130 cm by Giovanni BOLDINI (1845–1931) Courtesy Johannesburg Art Gallery Lady Phillips 1909 Oil on canvas 89 x 75 cm by Antonio Mancini (1852–1930) Courtesy Johannesburg Art Gallery Sir Lionel Phillips, 1st Baronet (6 August 1855 – 2 July 1936) was a British-born South African financier, mining magnate and politician. Early life Phillips was born in London on 6 August 1855 to Phillip Phillips, a tra...

Interest rate taking inflation into account Yields on inflation-indexed government bonds of selected countries and maturities. The real interest rate is the rate of interest an investor, saver or lender receives (or expects to receive) after allowing for inflation. It can be described more formally by the Fisher equation, which states that the real interest rate is approximately the nominal interest rate minus the inflation rate. If, for example, an investor were able to lock in a 5% interest...

Rothbury riotDate16 December 1929LocationRothbury Colliery32°40′49″S 151°20′44″E / 32.68024°S 151.34545°E / -32.68024; 151.34545 (Memorial)CasualtiesDeath(s)1 The Rothbury riot memorial Rothbury riot memorial On 16 December 1929 New South Wales Police drew their revolvers and shot into a crowd of locked-out miners in the New South Wales town of Rothbury in Australia, killing a 29-year-old miner, Norman Brown, and injuring approximately forty-five m...

Contea di DawsonconteaContea di Dawson – VedutaIl tribunale della contea di Dawson. LocalizzazioneStato Stati Uniti Stato federato Texas AmministrazioneCapoluogoLamesa Data di istituzione1876 TerritorioCoordinatedel capoluogo32°44′24″N 101°57′00″W / 32.74°N 101.95°W32.74; -101.95 (Contea di Dawson)Coordinate: 32°44′24″N 101°57′00″W / 32.74°N 101.95°W32.74; -101.95 (Contea di Dawson) Superficie2 336 km² Abitanti13&#...

1948 B-29 Waycross crashA B-29 Superfortress similar to the accident aircraftAccidentDate6 October 1948[1]SummaryFaulty maintenance[2]AircraftAircraft typeBoeing B-29 SuperfortressOperatorUnited States Air ForceRegistration45-21866Crew13Survivors4 (3 military, 1 civilian) The 1948 Waycross B-29 crash occurred on 6 October 1948[1] when an engine fire contributed to the crash of a Boeing B-29-100-BW Superfortress bomber in Waycross, Georgia. The plane was from the 3...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

Fauna and flora Bukhara deer pair, extremely endangered Central Asian deer The wildlife of Turkmenistan is the flora and fauna of Turkmenistan, and the natural habitats in which they live. Turkmenistan is a country in Central Asia to the east of the Caspian Sea. Two thirds of the country is hot dry plains and desert, and the rest is more mountainous. Very little rain falls in summer and the chief precipitation occurs in the southern part of the country in the winter and spring. The Caspian co...

Romanian and Albanian exonym for Bulgarians Aerial view of St. Nicholas Church, Șcheii Brașovului. Șchei (Bulgarian: шкеи, shkei) was an old Romanian exonym referring to the Bulgarians, especially in Transylvania and northern Wallachia. As a name, it has been preserved in the names of towns colonized in the 14th century by Bulgarians, in toponyms (Dealu Schiaului near Rășinari), hydronyms (Schiau River, tributary to the Argeş River), surnames (Schiau, Șchiau).[1] The word i...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Chopin Theatre – news · newspapers · books · scholar · JSTOR (June 2015) (Learn how and when to remove this message) Chopin TheatreAddress1543 W. Division StChicago, IL 60642USCoordinates41°54′11″N 87°40′0″W / 41.90306°N 87.66667°W&#...

خدعة ميرلين ، إدوارد برني-جونز, 1874 الخداع هو الترويج للاعتقاد بشيء غير حقيقي، أو ليس كل الحقيقة (كما في أنصاف الحقائق أو الإغفال). ويمكن أن يشمل التقية، البروباغندا، خفة اليد، الإلهاء، التمويه، أو الإخفاء. وهنالك أيضاً خداع النفس، كما في سوء النية. الخداع اعتداء كبير في العل...

Village in Florida, United StatesIndiantown, FloridaVillageVillage of IndiantownSW Warfield Blvd. SealMotto: Where Great Things GrowLocation in Martin County and the state of FloridaCoordinates: 27°2′N 80°28′W / 27.033°N 80.467°W / 27.033; -80.467Country United StatesState FloridaCounty MartinSettledCirca 1890sIncorporatedDecember 31, 2017Government • TypeMayor-Council • MayorSusan Gibbs Thomas • Vice May...

Disambiguazione – Se stai cercando altri significati, vedi Valencia (disambigua). ValenciacomuneValència Valencia – Veduta LocalizzazioneStato Spagna Comunità autonoma Valencia ProvinciaValencia AmministrazioneAlcaldeMaría José Catalá Verdet (PP) dal 17-6-2023 TerritorioCoordinate39°29′N 0°22′W39°29′N, 0°22′W (Valencia) Altitudine16 m s.l.m. Superficie134,65 km² Abitanti807 693[3] (2023) Densità5 998,46 ab./km² C...

Mauser BK-27 The Mauser BK-27 Jenis Revolver cannon Negara asal Germany Sejarah pemakaian Digunakan oleh See users Sejarah produksi Perancang Mauser (now Rheinmetall) Tahun 1976 Produsen Mauser (now Rheinmetall) Diproduksi 1977-present Jumlah produksi 3,100~ Spesifikasi Berat 100 kg (220 pon 7 oz) Panjang 231 m (757 ft 10 in) Panjang laras 173 m (567 ft 7 in) Selongsong peluru 27x145 mm Kaliber 27 mm (1,063 in) calibe...

Barista (Berita Artis Ternama)GenreInfotainmenPengisi suaraLady MarlinaNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim5Jmlh. episode586 (berjalan 16 Juli 2023)ProduksiDurasi60 menit (11::00-12:00 WIB)Rilis asliJaringanRCTIRilisSabtu, 4 November 2017 –sekarang Barista (Berita Artis Ternama) adalah sebuah acara televisi berformat infotainmen di RCTI. Acara ini mengungkapkan fakta-fakta berupa seputar kehidupan para artis selebriti, atau tragedi yang mengguncang kehidupan. Aca...

Moby ZazàMoby Zazà a Bastia nel 2017Descrizione generale Tipotraghetto ro-ro passeggeri ArmatoreMoby Lines ProprietàMoby S.p.A. Registro navaleRINA n° 90559 Porto di registrazione Amburgo (1982-1990) Oslo (1990-1994) Kristiansand (1994-2008) Helsinki (2008-2009) Hamilton (2009-2012) Londra (2012-2015) Livorno (2015- ) Identificazionenominativo internazionale ITU: IBLY(India-Bravo-Lima-Yankee) numero MMSI: 247369700numero IMO: 8020642 RottaLivorno - Bastia CostruttoriAG Weser Seebeckswerft...




































