Faktorisierungsmethode von Lehman
|
Read other articles:

Michel OnfrayLahir1 Januari 1959EraFilsafat abad ke-20, abad ke-21KawasanFilsafat barat, filsafat kontinentalAliranAteisme, Hedonisme, PostanarkismeMinat utamaAteisme, agama, etika, mazhab Kirene, Epikureanisme, kesenangan, sejarah filsafat, materialisme, estetika, bioetika Dipengaruhi Demokritus, Aristippus, Epikouros, Friedrich Nietzsche, anarkisme individualis, Georges Bataille, Michel de Montaigne, Han Ryner, Gilles Deleuze, Pierre Hadot, Julien Offray de La Mettrie, Michel Foucault...

Fadia Arafiq Bupati Pekalongan ke-24PetahanaMulai menjabat 27 Juni 2021PresidenJoko WidodoGubernurGanjar PranowoNana Sudjana (Pj.)WakilRiswadi PendahuluAsip KholbihiPenggantiPetahana Wakil Bupati Pekalongan ke-3Masa jabatan2011–2016PresidenSusilo Bambang Yudoyono Joko WidodoGubernurBibit Waluyo Ganjar PranowoBupatiAmat Antono PendahuluH. Wahyudi Pontjo NugrohoPenggantiIr. Hj. Arini Harimurti Informasi pribadiLahirLaila Fathiah23 Mei 1978 (umur 45)Jakarta, IndonesiaKebangsaa...

Constituency of Bangladesh's Jatiya Sangsad Narayanganj-1Constituencyfor the Jatiya SangsadDistrictNarayanganj DistrictDivisionDhaka DivisionCurrent constituencyCreated1996PartyAwami LeagueMember(s)Golam Dastagir Gazi Narayanganj-1 is a constituency represented in the Jatiya Sangsad (National Parliament) of Bangladesh since 1996. Current Member of Parliament of this constituency Golam Dastagir Gazi of the Awami League.[1] Boundaries The constituency encompasses Rupganj Upazila of Nara...
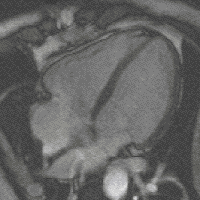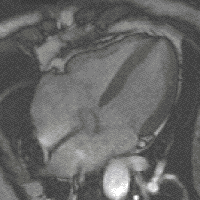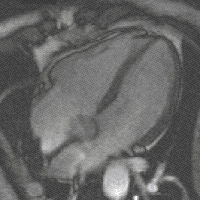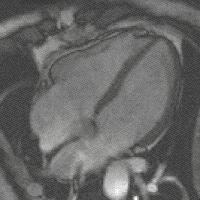
4 chamber cardiac magnetic resonance imaging using SSFP cine imaging. Steady-state free precession (SSFP) imaging is a magnetic resonance imaging (MRI) sequence which uses steady states of magnetizations. In general, SSFP MRI sequences are based on a (low flip angle) gradient echo MRI sequence with a short repetition time which in its generic form has been described as the FLASH MRI technique. While spoiled gradient-echo sequences refer to a steady state of the longitudinal magnetization only...

Lego themed resort in Goshen, New York, United States Legoland New York ResortLocationGoshen, New York, United StatesStatusOperatingOpenedMay 29, 2021; 2 years ago (2021-05-29)[a]OwnerMerlin Entertainments[1]Operated byMerlin EntertainmentsThemeLegoArea150 acres (61 ha) on 500 acres (200 ha)AttractionsTotal17Roller coasters2Water rides4Websitehttps://www.legoland.com/new-york/ Legoland New York Resort is a theme park in Goshen, New York owned by Mer...

الوليد بن عبد الملك الوليد بن عبد الملك بن مروان بن الحكم بن أبي العاص بن أمية نقش لاسم أمير المؤمنين الوليد بن عبد الملك الخليفة الأموي السادس معلومات شخصية الميلاد 668 (46 هـ)المدينة المنورة الوفاة 715 (96 هـ) (50 سنة)دير مروان، غوطة دمشق مكان الدفن دمشق مواطنة الدولة الأموية ...

Submarine service of the People's Liberation Army Navy Flag of the People's Liberation Army Navy (PLAN) The People's Liberation Army Navy Submarine Force (PLANSF) is the submarine service of the People's Liberation Army Navy. It consists of all types of submarines in operational service organized into three fleets: the North Sea Fleet, the East Sea Fleet, and the South Sea Fleet. Submarines have long been one of the three focuses of the People's Liberation Army Navy (the other two are aircraf...

Ulysses S. Grant IIILahir(1881-07-04)4 Juli 1881Chicago, Illinois, ASMeninggal29 Agustus 1968(1968-08-29) (umur 87)Clinton, New York, ASPengabdian Amerika SerikatDinas/cabang Angkatan Darat Amerika SerikatLama dinas1903–1946Pangkat Mayor jenderalKomandan1st Engineer RegimentEngineer Replacement Training CenterOffice of Civilian DefensePerang/pertempuranPerang Filipina-AmerikaPerang Dunia IPerang Dunia IIPenghargaanDistinguished Service MedalLegion of MeritLégion d'honneurCro...

Deputy military head of the United States Space Force Vice Chief of Space OperationsSpace Staff Identification BadgeFlag of the Vice Chief of Space OperationsIncumbentGeneral Michael Guetleinsince 21 December 2023United States Space ForceSpace StaffAbbreviationVCSOMember ofSpace StaffJoint Requirements Oversight CouncilReports toSecretary of the Air ForceChief of Space OperationsSeatThe Pentagon, Arlington County, Virginia, United StatesAppointerThe Presidentwith Senate advice and consen...

منتخب بوليفيا لكرة القدم (بالإسبانية: Selección nacional de fútbol de Bolivia) معلومات عامة بلد الرياضة بوليفيا الفئة كرة القدم للرجال رمز الفيفا BOL الاتحاد اتحاد بوليفيا لكرة القدم كونفدرالية كونميبول (أمريكا الجنوبية) الملعب الرئيسي ملعب هيرناندو سيليس الموقع الرسمي المو...

455th Air Expeditionary Wing A C-17 Globemaster III takes off from Bagram Airfield near C-130 Hercules deployed with the wingActive1943–1945; 1947–1949; 1956–1957; 1962–1968; 2002–2021Country United StatesBranch United States Air ForceTypeAir ExpeditionaryRoleCombat & Combat SupportPart ofUnited States Air Forces Central CommandGarrison/HQBagram Airfield, AfghanistanNickname(s)Vulgar Vultures (World War II)[1]EngagementsMediterranean Theater of Operations...

ブガッティ・18/3の3バンク式W型18気筒エンジン W型18気筒(ダブリュがたじゅうはちきとう)はピストン式内燃機関(レシプロエンジン)のシリンダー配列形式の一つで、W型エンジンの一種。W18と略される事もある。 レイアウト 通常は直列6気筒エンジンを60度ないし90度のバンク角度で3列に配置した3バンク式のレイアウトが採用される事が多い。それ故に他の3バンク式...

العلاقات الباهاماسية الغينية باهاماس غينيا باهاماس غينيا تعديل مصدري - تعديل العلاقات الباهاماسية الغينية هي العلاقات الثنائية التي تجمع بين باهاماس وغينيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة...

城中之城类型金融、商戰、反腐编剧卞智弘、吳楠、田雨导演滕華濤[1]主演白宇帆、于和偉、夏夢、隆妮、王驍、馮嘉怡、楊子姍、王勁松、陳瑾、塗松岩[2]国家/地区 中国大陆语言汉语普通话集数40集每集长度45分鐘制作制作人馬駿、楊蓓、楊文紅出品人薛繼軍、龔宇、李向東、楊文紅拍攝地點上海[3]播出信息 首播频道央視一套、愛奇藝播出日期2024年4月...

Canadian volleyball player Jaimie ThibeaultPersonal informationNationality CanadaBorn (1989-09-23) 23 September 1989 (age 35)HometownRed Deer, AlbertaHeight1.88 m (6 ft 2 in)Spike302 cm (119 in)Block286 cm (113 in) Jaimie Thibeault (born 23 September 1989) is a Canadian volleyball player. She is a member of the Canada women's national volleyball team. She was part of the Canadian national team at the 2014 FIVB Volleyball Women's World Championship ...
Perceived increase in the rate of technological change throughout history This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2020) (Learn how and when to remove this message) This article needs additional cita...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Stockholm during the early Vasa era – news · newspapers · books · scholar · JSTOR (February 2008) Image from Triumph of Vasa, showing Gustav Vasa besieging Stockholm. in 1521. Stockholm during the early Vasa era (1523–1611) is a period in the hi...

Foramadiahi is a village on Ternate island in North Maluku, Indonesia. It has a prominent role in stories about the formation of the Ternate Kingdom and has a number of historical graves.[1] The grave of Sultan Babullah in Foramadiahi Foramadiahi is situated in the southern part of Ternate, 350 meters above sea level, overlooking the old sultan's seat Gam-ma-lamo. According to the historical traditions of Ternate, the oldest center on the island was Tobona further uphill. In the mid-1...

国際通貨基金 各国語表記 International Monetary Fund(英語)Fonds monétaire international(フランス語)Международный валютный фонд(ロシア語)国际货币基金组织(中国語)Fondo Monetario Internacional(スペイン語)صندوق النقد الدولي(アラビア語) シンボルマーク IMF本部概要 専門機関略称 IMF代表 クリスタリナ・ゲオルギエヴァ(英語版)専務理事状況 活動中活�...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يونيو 2020) لغات باكستان تعديل مصدري - تعديل يوجد في باكستان عدة لغات و تبقى اللغة الأردية هي اللغة الرسمية للدولة....
![{\displaystyle {\sqrt[{3}]{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b780c7060d1bc0ab596390e950dc537cee82af1a)





![{\displaystyle \lfloor {\sqrt[{3}]{n}}\rfloor }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8026f7192fd30b29beea890a9da7e7b6f5be13f7)

![{\displaystyle \lfloor {\sqrt {4kn}}+{\frac {\sqrt[{6}]{n}}{4{\sqrt {k}}}}\rfloor }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9041e88ada9517a3b3d93395a5d6fd3fc9254e66)















