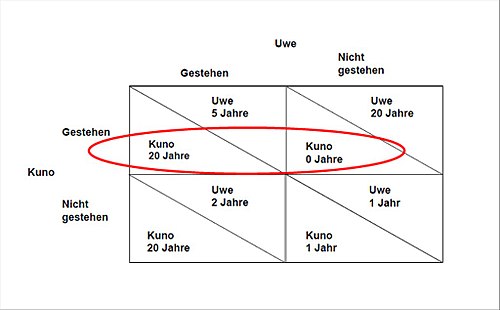
Dominante Strategie
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Yiu Chung-yimMHKIS, FRICS姚松炎Edward Yiu pada 2017. Anggota Dewan LegislatifMasa jabatan1 Oktober 2016 – 12 Oktober 2016 PendahuluTony TsePenggantiTony Tse Informasi pribadiLahir19 Juli 1964 (umur 59)Hong KongPendidikanSekolah Tekn...

Willis LambNobel foundation, 1955Lahir(1913-07-12)12 Juli 1913Los Angeles, California, Amerika SerikatMeninggal15 Mei 2008(2008-05-15) (umur 94)Tucson, Arizona, Amerika SerikatKebangsaanAmerika SerikatAlmamaterUniversity of California, BerkeleyDikenal atasperpindahan LambPenghargaanNobel Fisika (1955)Karier ilmiahBidangFisikaInstitusiUniversity of ArizonaUniversity of OxfordYale UniversityColumbiaStanford UniversityPembimbing doktoralJulius Robert OppenheimerMahasiswa doktoralMarlan Scu...

Radio station in Spearman, TexasKXDJSpearman, TexasBroadcast areaAmarillo, TexasFrequency98.3 MHzProgrammingFormatCountryOwnershipOwnerChris SamplesHistoryFormer call signsKBMF-FM (1963-1978)KRDF-FM (1978-2005)Technical informationFacility ID61684ClassC2ERP17,500 WattsHAAT255.0 meters (836.6 ft)Transmitter coordinates36°3′44.00″N 101°1′56.00″W / 36.0622222°N 101.0322222°W / 36.0622222; -101.0322222LinksWebsitehttp://www.kxdjradio.com KXDJ (98.3 FM) is ...

Speech by US president George W. Bush 2004 State of the Union AddressPresident George W. Bush during the speech, with Vice President Dick Cheney and House Speaker Dennis Hastert behind himDateJanuary 20, 2004 (2004-01-20)Time9:00 p.m. ESTDuration53 minutesVenueHouse Chamber, United States CapitolLocationWashington, D.C.Coordinates38°53′19.8″N 77°00′32.8″W / 38.888833°N 77.009111°W / 38.888833; -77.009111TypeState of the Union AddressPart...

Amerika Serikat (hijau) dan misi diplomatiknya, termasuk kedutaan besar (biru), bagian kepentingan dan perwakilan lainnya (biru muda) Amerika Serikat memiliki misi diplomatik terbanyak kedua di dunia, setelah Tiongkok,[1] yaitu sebanyak 166 dari 193 negara anggota PBB dan negara pengamat Kota Vatikan serta negara-negara non-anggota PBB Kosovo dan Taiwan. Selain itu, Amerika Serikat juga memiliki kantor bagian kepentingan di kantor kedutaan negara lain di Iran dan Suriah. Afrika Amerik...
Broadsheet newspaper in Spokane, Washington, United States The Spokesman-ReviewTypeDaily newspaperFormatBroadsheetOwner(s)Cowles CompanyPublisherWilliam Stacey CowlesEditorRob Curley[1]FoundedJune 29, 1894; 129 years ago (1894-06-29) in Spokane, Washington, U.S. (merger)LanguageEnglishHeadquarters999 W. Riverside Ave.Spokane, WashingtonCountryUnited StatesCirculation56,629 (as of 2022)[2]ISSN2993-1274OCLC number11102529 Websitespokesman.comMedia of the Un...

此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

Dislike of Lithuania, its people and culture Part of a series onDiscrimination Forms Institutional Structural Attributes Age Caste Class Dialect Disability Genetic Hair texture Height Language Looks Mental disorder Race / Ethnicity Skin color Scientific racism Rank Sex Sexual orientation Species Size Viewpoint Social Arophobia Acephobia Adultism Anti-albinism Anti-autism Anti-homelessness Anti-drug addicts Anti-intellectualism Anti-intersex Anti-left handedness Anti-Masonry Antisemit...

301st Operations Group457th Fighter Squadron F-16s taking off from Carswell FieldActive3 February 1942 – presentCountry United StatesBranch United States Air ForceTypeGroupRoleFighterPart of Air Force Reserve CommandGarrison/HQCarswell Field, Naval Air Station Joint Reserve Base Fort Worth, TexasTail CodeTexas flag tail stripe TX Texas LonghornsEngagements World War II – American Campaign (Antisubmarine) World War II – EAME Theater Decorations Distinguished Unit Ci...

« American Civil War » redirige ici. Pour le jeu vidéo, voir AGEOD's American Civil War. Guerre de Sécession En haut à gauche, la bataille de la Stones River ; en haut à droite, prisonniers confédérés se désaltérant à Gettysburg ; en bas, la bataille de Fort Hindman. Informations générales Date Du 12 avril 1861 au 9 avril 1865[note 1](3 ans, 11 mois et 28 jours) Lieu Principalement dans le sud-est des États-Unis Casus belli Bombardement de Fo...

1928 Chinese Communist Party conferenceNot to be confused with 6th National People's Congress.You can help expand this article with text translated from the corresponding article in Chinese. (July 2021) Click [show] for important translation instructions. View a machine-translated version of the Chinese article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation...

Dialogue, attributed to Plato, of Clitophon to Socrates Part of a series onPlatonism Life Theory of forms Form of the Good Theory of soul Epistemology Political philosophy Euthyphro dilemma Demiurge Atlantis The Republic Allegory of the cave Analogy of the Sun Analogy of the divided line Philosopher king Ship of State Ring of Gyges Myth of Er The works of Plato Euthyphro Apology Crito Phaedo Cratylus Theaetetus Sophist Statesman Parmenides Philebus Symposium Phaedrus First Alcibiades Second A...

Capital and largest city of Romania Not to be confused with Budapest. Capital city and municipality in București – Ilfov, RomaniaBucharest BucureștiCapital city and municipalityCity of BucharestRomanian AthenaeumPalace of ParliamentCentral University LibraryPalace of JusticeFloreascaCEC PalaceKing Michael I ParkBucharest Old TownCity Gate Towers FlagCoat of armsLogoNicknames: Paris of the East / Little ParisMotto(s): Patria și dreptul meu(The Homeland and my right)Bucharest hig...

Pour les articles homonymes, voir aube. Aube Église de l'Assomption-de-la-Bienheureuse-Vierge-Marie d'Aube. Héraldique Administration Pays France Région Grand Est Département Moselle Arrondissement Metz Intercommunalité Communauté de communes du Sud Messin Maire Mandat Jean-Christophe Moulon 2020-2026 Code postal 57580 Code commune 57037 Démographie Gentilé Aubois, Auboises Populationmunicipale 265 hab. (2021 ) Densité 50 hab./km2 Géographie Coordonnées 49° 01′&#...

24°15′N 120°40′E / 24.250°N 120.667°E / 24.250; 120.667 「台中」重定向至此。关于與這些名稱相似的其他條目,请见「臺中 (消歧义)」。 臺中市Taichung City簡稱:臺中、中市直轄市從上至下、由左至右:臺灣大道與臺中市區天際線、南湖大山、路思義教堂、國立自然科學博物館植物園、臺中火車站、高美野生動物保護區、臺中洲際棒球場 市旗市徽 ...

American boxer Billy PetrolleBornWilliam Michael Petrolle(1905-01-10)January 10, 1905Berwick, Pennsylvania, United StatesDiedMay 14, 1983(1983-05-14) (aged 78)Other namesThe Fargo ExpressStatisticsWeight(s)LightweightHeight5 ft 7 in (1.70 m)Reach70 in (178 cm)StanceOrthodox Boxing recordTotal fights164Wins122Wins by KO65Losses26Draws15No contests1 William Michael Petrolle (January 10, 1905 – May 14, 1983) was a world lightweight boxing title contender. Boxing ra...

Kota TinggiKotaNegara MalaysiaNegara bagianJohorDistrikKota Tinggi Kota Tinggi adalah sebuah kota kecil di Distrik Kota Tinggi, Johor, Malaysia. Kota ini sendiri kurang menarik, tetapi air terjun di Lumbong, terletak 15 kilometer barat laut kota merupakan tujuan wisata terkenal. Air terjun itu setinggi 36 meter, dan terletak di kaki ketinggian 634 Gunung Muntahap. Sungai mengalir melalui rangkaian tempat yang dangkal yang bagus untuk berenang. Keindahan alam tempat ini telah agak rusak oleh p...

US Open 1978Sport Tennis Data28 agosto - 10 settembre Edizione98ª CategoriaGrande Slam (ITF) SuperficieCemento LocalitàNew York negli Stati Uniti ImpiantoUSTA Billie Jean King National Tennis Center, Flushing Meadows CampioniSingolare maschile Jimmy Connors Singolare femminile Chris Evert Doppio maschile Bob Lutz / Stan Smith Doppio femminile Billie Jean King / Martina Navrátilová Doppio misto Betty Stöve / Frew McMillan 1977 1979 Lo US Open 1978 è stata la 98ª edizione dello US Open e...
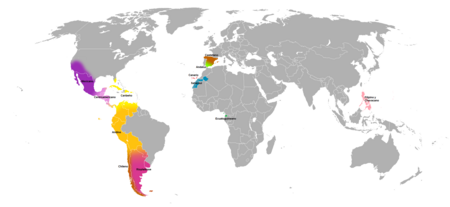
スペイン語の主な変種。 黄色がカリブ・スペイン語 カリブ・スペイン語(カリブ・スペインご、スペイン語: español caribeño)は、大アンティル諸島とカリブ海沿岸で有力なスペイン語の方言である。キューバ、ドミニカ共和国、プエルト・リコといった島の領域と、ベネズエラ、コロンビア、パナマといった大陸の領域で話される。 アンダルシア方言(港間での歴�...

北極百貨店のコンシェルジュさん 漫画 作者 西村ツチカ 出版社 小学館 掲載誌 ビッグコミック増刊号 レーベル ビッグコミックススペシャル 発表号 2017年3月号[注 1] - 2018年12月号[注 2] 巻数 全2巻 映画 原作 西村ツチカ 監督 板津匡覧 脚本 大島里美 キャラクターデザイン 森田千誉 音楽 tofubeats 制作 Production I.G 配給 アニプレックス 封切日 2023年10月20日 上映�...