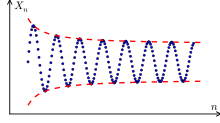
Cauchy-Folge
|
Read other articles:

This article is about the hypothalamic structure. For the structure in the medulla oblongata, see Arcuate nucleus (medulla). Arcuate nucleusArcuate nucleus is 'AR', at bottom center, in green.DetailsPart ofHypothalamusIdentifiersLatinnucleus arcuatus hypothalamiMeSHD001111NeuroNames395NeuroLex IDbirnlex_1638TA98A14.1.08.923TA25726FMA62329Anatomical terms of neuroanatomy[edit on Wikidata] The arcuate nucleus of the hypothalamus (also known as ARH,[1] ARC,[2] or infundibular...

Untuk porsi Kota Kansas di Kansas, lihat Kota Kansas, Kansas. Kota Kansas MissouriKota BenderaJulukan: KC, KCMO, the City of Fountains, Paris of the Plains, and the Heart of AmericaCity boundaries and location within the U.S.Koordinat: 39°05′59″N 94°34′42″W / 39.09972°N 94.57833°W / 39.09972; -94.57833Koordinat: 39°05′59″N 94°34′42″W / 39.09972°N 94.57833°W / 39.09972; -94.57833Negara Amerika SerikatNegara bagia...

العلاقات البوروندية التونسية بوروندي تونس بوروندي تونس تعديل مصدري - تعديل العلاقات البوروندية التونسية هي العلاقات الثنائية التي تجمع بين بوروندي وتونس.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة بو�...

Species of bat Rendall's serotine Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Chiroptera Family: Vespertilionidae Genus: Pseudoromicia Species: P. rendalli Binomial name Pseudoromicia rendalli(Thomas, 1889) Synonyms Vesperugo (Vesperus) rendalli Thomas, 1889 Eptesicus rendalli (Thomas, 1889) Neoromicia rendalli Rendall's serotine (Pseudoromicia rendalli) is a species of...

Machine learning software library MindSporeDeveloper(s)HuaweiInitial releaseMarch 31, 2020; 4 years ago (2020-03-31)Repositorygithub.com/mindspore-ai/mindsporeWritten inC++, Rust, Julia, Python, ArkTS, Cangjie, Java (Lite)PlatformLinux, Microsoft Windows, EulerOS, openEuler, OpenHarmony, Oniro OS, HarmonyOS, AndroidTypeMachine learning libraryLicenseApache License 2.0Websitewww.mindspore.cn/en Part of a series onMachine learningand data mining Paradigms Supervised learning U...

مدينة كبيرةمعلومات عامةصنف فرعي من مدينة أو بلدةمستوطنة حضريةتقسيم إداري الاسم المختصر г. (بالروسية) ш. (بالطاجيكية) қ. (بالقازاقية) الرتبة الأدنى التالية مدينة يدرسه دراسات حضريةتاريخ حضري جغرافيا هذا الموضوع جغرافيا حضرية لديه جزء أو أجزاء حي سكني تصنيف للتصنيفات التي تح...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 ...

The Judiciary of Azerbaijan exercises judicial power in Azerbaijan. Although the Azerbaijan constitution nominally guarantees judicial independence, the executive firmly controls prosecutors and judges.[1] Judges and prosecutors collaborate in Azerbaijan to repress political opponents.[1] Source of the judicial power in Azerbaijan The Azerbaijan constitution holds that state power in the Republic of Azerbaijan is formed on the principle of separation of powers[2] where...

Brussoncomune(IT) Comune di Brusson(FR) Commune de Brusson Brusson – VedutaPanorama di Brusson LocalizzazioneStato Italia Regione Valle d'Aosta ProvinciaNon presente AmministrazioneSindacoDanilo Grivon (Brusson Unito) dal 23-9-2020 Lingue ufficialiFrancese, italiano TerritorioCoordinate45°46′N 7°44′E / 45.766667°N 7.733333°E45.766667; 7.733333 (Brusson)Coordinate: 45°46′N 7°44′E / 45.766667°N 7.733333°E45.766667; 7.7333...

Australian politician John Fitzgerald Burns, 1875 engraving John Fitzgerald Burns (1833 – 19 March 1911)[1] was an Australian politician, member of the Parliament of New South Wales, Postmaster-General in the 1870s and Colonial Treasurer in the 1880s. Burns was born in the north of Ireland, and emigrated to New South Wales at an early age.[2] In 1854 he married Lucy Maria Smith at Maitland.[1] Having engaged in mercantile pursuits in the Hunter River district, Burns ...

Caspar David Friedrich Retrato de Caspar David Friedrich por Gerhard von Kügelgen, c. 1810–1820.Información personalNacimiento 5 de septiembre de 1774Greifswald, Pomerania SuecaFallecimiento 7 de mayo de 1840 (65 años)Dresde, Reino de SajoniaSepultura Cementerio de la TrinidadNacionalidad AlemanaReligión Luteranismo FamiliaPadres Adolph Gottlieb Friedrich Sophia Dorothea Bechly Cónyuge Christiane Caroline BommerHijos Emma Friedrich Agnes Adelheid Friedrich Gustav Adolf FriedrichEd...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

1992 Austrian presidential election ← 1986 26 April 1992 (first round)24 May 1992 (second round) 1998 → Nominee Thomas Klestil Rudolf Streicher Party Independent (ÖVP) SPÖ Popular vote 2,528,006 1,915,380 Percentage 56.89% 43.11% Second round First round President before election Kurt Waldheim Independent (ÖVP) Elected President Thomas Klestil Independent (ÖVP) This article is part of a series on thePolitics of Austria Law Constitution (B-VG) Taxation Sta...

Post-split Iraqi Ba'athist political party This article is about the branch that controlled Iraq. For the pan-Arab Ba'ath Party, which is Iraqi-led but has branches in multiple countries, see Ba'ath Party (Iraqi-dominated faction). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is missing information about the party's activities after 2012. Please expand the article to inclu...

Mental health facility United States historic placeUtica State Hospital, Main BuildingU.S. National Register of Historic PlacesU.S. National Historic LandmarkNew York State Register of Historic Places Show map of New YorkShow map of the United StatesLocation1213 Court Street, Utica, New York 13502Coordinates43°06′18″N 75°15′13″W / 43.10496225°N 75.25347233°W / 43.10496225; -75.25347233Built1843ArchitectCapt. William Clarke, Andrew Jackson DowningArchitectur...

صربيا في مواجهة بلجيكا يوم 12 أكتوبر 2012. تصفيات كأس العالم لكرة القدم 2014 – أوروبا المجموعة أ كانت واحدة من مجموعات التصفيات الأوروبية المؤهلة إلى كأس العالم لكرة القدم 2014. تألفت المجموعة من بلجيكا وكرواتيا ومقدونيا واسكتلندا وصربيا وويلز. تأهلت المنتخب البلجيكي متصدر المج�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: McCauley Weir – news · newspapers · books · scholar · JSTOR (October 2021) (Learn how and when to remove this message) Reservoir in South East of Nanango, QueenslandLake McCauleyMcCauley Weir (September 2001)Lake McCauleyLocation5 km (3 mi) South Eas...

Adelaide Jubilee International ExhibitionOverviewBIE-classUnrecognized expositionNameAdelaide Jubilee International ExhibitionBuilding(s)Jubilee Exhibition BuildingArea18 acresVisitors766,880Participant(s)Countries26LocationCountryAustraliaCityAdelaide, South AustraliaVenueNorth TerraceCoordinates34°55′14″S 138°36′22″E / 34.920544°S 138.606188°E / -34.920544; 138.606188TimelineOpening21 June 1887Closure7 January 1888 The Adelaide International Jubilee Exhi...

1960年夏季奥林匹克运动会奖牌榜地点 意大利羅馬摘要金牌数最多 苏联(43)银牌数最多 苏联(29)铜牌数最多 苏联(31)奖牌总数最多 苏联(103) ← 1956 奥林匹克运动会奖牌榜 1964 → 1960年夏季奥林匹克运动会奖牌榜 名次 编码 队伍 金牌 银牌 铜牌 总数 总数排名 1 URS 苏联 43 29 31 103 ' 2 USA 美国 34 21 16 71 ' 3 ITA 意大利 13...

Painter from the Northern Netherlands (c. 1582–1666) Frans HalsCopy of a Self-portrait by HalsBornc. 1582Antwerp, Flanders, Spanish NetherlandsDied26 August 1666(1666-08-26) (aged 83–84)Haarlem, Dutch RepublicNationalityDutchNotable workThe Gypsy Girl (1628)Laughing Cavalier (1624)Laughing Boy (c. 1625)Signature Frans Hals the Elder (UK: /hæls/,[1] US: /hɑːls, hælz, hɑːlz/;[2][3][4] Dutch: [frɑns ˈɦɑls]; c. 1582 – ...