Bedingte Entropie
|
Read other articles:

Emma RobertsRoberts di San Diego Comic-Con International tahun 2016LahirEmma Rose Roberts10 Februari 1991 (umur 33)Rhinebeck, New York, Amerika SerikatPekerjaanAktrisPenyanyiTahun aktif2001–sekarangAnak1KerabatJulia Roberts (Bibi) Emma Rose Roberts (lahir 10 Februari 1991)[1] adalah seorang aktris dan penyanyi asal Amerika Serikat. Setelah membuat debut filmnya sebagai Kristina Jung dalam film kejahatan, Blow (2001), Roberts mulai dikenali untuk peran utamanya sebagai Add...

Aku Lupa Aku LukaSutradaraDyan Sunu PrastowoProduser Agung Haryanto Karli Surya Winata SkenarioEimiria TamsyarinaPemeran Junior Roberts Salshabilla Adriani Dewa Dayana Jerome Kurnia Penata musikGanden BramantoSinematograferRaden Gama HardianPenyuntingJoned WirawanPerusahaanproduksi KlikFilm Productions Canary Studios Limelight Pictures DistributorKlikFilmTanggal rilis 8 Oktober 2021 (2021-10-08) (Indonesia) Durasi60 menitNegaraIndonesiaBahasaBahasa Indonesia Aku Lupa Aku Luka a...

العلاقات الإكوادورية الميكرونيسية الإكوادور ولايات ميكرونيسيا المتحدة الإكوادور ولايات ميكرونيسيا المتحدة تعديل مصدري - تعديل العلاقات الإكوادورية الميكرونيسية هي العلاقات الثنائية التي تجمع بين الإكوادور وولايات ميكرونيسيا المتحدة.[1][2][3&#...
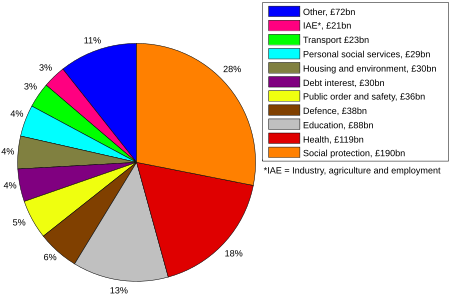
Welfare Programs in the United Kingdom This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs attention from an expert in Sociology. The specific problem is: The article needs a broader understanding of the historical context and social climate that gave rise to the Welfare State in Britain. WikiProject Sociology may be able to help recruit an expert. (October 2020) This arti...
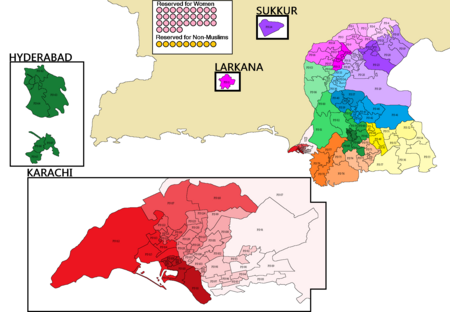
Constituency of the Provincial Assembly of Sindh, Pakistan PS-45 Mirpur Khas-IConstituencyfor the Provincial Assembly of SindhRegionHussain Bux Mari Tehsil and Mirpur Khas Tehsil (partly) including Mirpur Khas city in Mirpur Khas DistrictElectorate243,176 [1]Current constituencyMember(s)VacantCreated fromPS-64 Mirpurkhas-I (2002-2018) PS-47 Mirpur Khas-I (2018-2023) PS-45 Mirpur Khas-I (پی ایس-45، مِيرپورخاص-1) is a constituency of the Provincial Assembly of Sindh.[...

American TV series or program George Washington II: The Forging of a NationGenreDramaWarWritten byJames Thomas Flexner (book)Richard FielderDirected byWilliam A. GrahamStarringBarry BostwickPatty Duke AstinTheme music composerBruce BroughtonCountry of originUnited StatesOriginal languageEnglishNo. of episodes2ProductionExecutive producerDavid GerberProducersRichard FielderRobert Hargrove (supervising producer)Production locationsColonial Williamsburg, Williamsburg, VirginiaMount Vernon Estat...

ما قبل الرفائيليةمعلومات عامةالفترة الزمنية العصر الفيكتوري البداية 1848 المؤسس ويليام هنت — جون إيفرت ميليه — دانتي جابرييل روزيتي التأثيراتتأثرت بـ جون راسكن تعديل - تعديل مصدري - تعديل ويكي بيانات لوحة بروسيربن للفنان دانتي جابرييل روزيتي دانتي وبياتريس في الحديقة ، 1903...

Port การท่าเรือ เอฟซีBerkas:Port FC logo.svgNama lengkapPort Football Club สโมสรฟุตบอล การท่าเรือJulukanPort Lions (tim) Khlong Toei Lions (supporter)Berdiri1967; 57 tahun lalu (1967) sebagai Port Authority of Thailand Football ClubStadionStadion PATKlong Toei, Bangkok, Thailand(Kapasitas: 8,000)PemilikMuang Thai Insurance Port Authority of ThailandKetuaChalermchoke LamsamPelatihRangsan ViwatchaichokLigaLiga Thailand...

L'uxoricide (du latin uxor : « épouse » et -cide, de caedere : « couper, tuer ») est le meurtre d'une femme par son conjoint ou son compagnon. Le terme peut désigner aussi bien l'acte lui-même que la personne qui le commet[1]. C'est une forme spécifique de féminicide[2]. Fréquence des uxoricides Le suicide du Galate, ou Galate se donnant la mort après avoir tué sa femme, palazzo Altemps à Rome. D'après l'Organisation mondiale de la santé, en Asie d...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

American singer, actor, and dancer Barrett FoaFoa in 2015Born (1977-09-18) September 18, 1977 (age 46)Manhattan, New York City, New York, U.S.Alma materUniversity of MichiganOccupation(s)Actor, singer, dancerYears active1995–present Barrett Conrad Foa (born September 18, 1977)[1] is an American singer, dancer, and actor, with over a decade in Broadway theatre shows.[2] He has played many leading characters in off-Broadway and regional theatre productions. He h...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

أساس التقديس كتاب تأسيس التقديس أو أساس التقديس/ تأليف شيخ المعقول والمنقول الإمام فخر الدين الرازي الذي انتقده ابن تيمية في كتابه بيان تلبيس الجهمية؛ ومعه رسالة الإمام العلامة أحمد بن يحيى بن جهبل الكلابي 733هـ في الرد على من رد على صاحب التأسيس. الاسم أساس التقديس العنوان...

Депортация поляков Советская и немецкая зоны оккупации Польши Страна СССР Исполнитель НКВД Место приграничные районы СССР Результат депортация осадников, беженцев, «социально чуждых элементов» Депортация поляков — массовое выселение поляков, оказавшихся на те�...

Pemandangan kota Yokosuka dari Taman Verny. Markas Angkatan Laut AS di Yokosuka. Yokosuka (bahasa Jepang: 横須賀市; -shi) adalah sebuah kota di Prefektur Kanagawa, Jepang. Kota ini terletak di mulut Teluk Tokyo di Semenanjung Miura, dan membentang sepanjang semenanjung tersebut hingga Teluk Sagami. Dikembangkan dan digunakan sebagai markas bagi Angkatan Laut Kekaisaran Jepang hingga 1945, Yokosuka kini adalah lokasi salah satu pelabuhan militer terbesar yang digunakan bersama antara Angk...

American jazz band This article is about The Jazz Messengers group. For the album, see The Jazz Messengers (1956 album). Art Blakey and the Jazz Messengers redirects here. For their self-titled albums, see Art Blakey and the Jazz Messengers (disambiguation). The Jazz MessengersThe Jazz Messengers in 1960. From left: Lee Morgan, Wayne Shorter (obscured), Jymie Merritt, and Art BlakeyBackground informationGenres Jazz hard bop bebop Years active1955 (1955)–1990 (1990)Labels A&M A...

Pintu Pohan MerantiKecamatanPeta lokasi Kecamatan Pintu Pohan MerantiNegara IndonesiaProvinsiSumatera UtaraKabupatenTobaPemerintahan • CamatJosten Sihotang, SHPopulasi • Total7,478 jiwa (2.019) jiwaKode Kemendagri12.12.05 Kode BPS1206071 Luas277,27 km²Desa/kelurahan7 Desa Pintu Pohan Meranti adalah salah satu kecamatan di Kabupaten Toba, Sumatera Utara, Indonesia. Geografi Kecamatan Pintu Pohan Meranti memiliki wilayah seluas 277,72 km2.[1] Persentase lua...

شون ستريكلاندستريكلاند في يو إف سي ليلة القتال 200الميلادشون ستريكلاند27 فبراير 1991 (العمر 33 سنة)آناهايم، كاليفورنيا، الولايات المتحدةالاسم المستعارطرزان (بالإنجليزية: Tarzan)الطول6 قدم 1 بوصة (1.85 م)الوزن185 رطل (84 كـغ؛ 13.2 ستون)الفئةالوزن المتوسط (2009–2015، 2020–الآ�...


















































![{\displaystyle \qquad =\textstyle {\frac {3}{4}}\cdot {\begin{matrix}\underbrace {H(X|Y=0)} \\{}^{\rm {H(\;P(X=0|Y=0)\;,\;P(X=1|Y=0)\;)}}\\[-4.5ex]\end{matrix}}+\textstyle {\frac {1}{4}}\cdot {\begin{matrix}\underbrace {H(X|Y=1)} \\{}^{\rm {H(\;P(X=0|Y=1)\;,\;P(X=1|Y=1)\;)}}\\[-4.5ex]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/723e3ced345320f7bae401111cb1f0585c84e43e)
![{\displaystyle \qquad =\textstyle {\frac {3}{4}}\cdot H(\textstyle {\frac {2}{3}},\textstyle {\frac {1}{3}})+{\begin{matrix}\textstyle {\frac {1}{4}}\cdot \underbrace {H(1,0)} \\{}^{\rm {=0}}\\[-4.5ex]\end{matrix}}=0{,}689\,bit}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7fd122f03f81048e77d9de63a8c1f0182505535)












![{\displaystyle =\textstyle {\frac {1}{2}}\cdot H(\textstyle {\frac {1}{2}}|\textstyle {\frac {1}{2}})+{\begin{matrix}\underbrace {\textstyle {\frac {1}{4}}\cdot H(1,0)} \\{}^{\rm {=0}}\\[-4.5ex]\end{matrix}}+{\begin{matrix}\underbrace {\textstyle {\frac {1}{4}}\cdot H(0|1)} \\{}^{\rm {=0}}\\[-4.5ex]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7101506ed0cd0763ffbbaa0e0426956ce000550)
















