Absolut konvergente Reihe
|
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: SMP Negeri 24 Surabaya – berita · surat kabar · buku · cendekiawan · JSTOR SMP Negeri 24 SurabayaInformasiDidirikan1983Rentang kelasVII, VIII, IXKurikulumKurikulum Tingkat Satuan PendidikanAlamatLokasiJl...

Untuk tokoh yang dijuluki Raden Pamanah Rasa hingga menjadi salah satu Raja Sunda Galuh, lihat Sri Baduga Maharaja. Raden Pamanah RasaGenre Drama Epos Laga Fantasi PembuatMNC PicturesBerdasarkanRaden Pamanah Rasaoleh Enang Rokajat AsuraSkenario Ichal Beng(Eps. 1—6) Rachmawati(Eps. 7—9) CeritaEnang Rokajat AsuraSutradaraDedy MercySutradara lagaAhmad PotabugaPemeran Ferdi Ali Bima Azriel Kirana Larasati Fatmasury Penggubah lagu temaAhmad DhaniLagu pembukaIman oleh Ahmad DhaniLagu penutupIma...

خالد بن عبد الله بن عبد الرحمن آل سعود معلومات شخصية الميلاد سنة 1937 الطائف تاريخ الوفاة 13 يناير 2021 (83–84 سنة)[1] مواطنة السعودية الزوجة الجوهرة بنت عبد العزيز آل سعود الأب عبد الله بن عبد الرحمن بن فيصل آل سعود عائلة آل سعود الحياة العملية المهنة �...

Noormiliyani Bupati Barito Kuala ke-12Masa jabatan4 November 2017 – 4 November 2022WakilRahmadian Noor PendahuluHasanuddin MuradPenggantiZulkipli Yadi Noor (plh.)Mujiyat (pj.)Ketua Dewan Perwakilan Rakyat Daerah Provinsi Kalimantan SelatanMasa jabatan1 Oktober 2014 – Oktober 2016[1] PendahuluNasib AlamsyahPenggantiBurhanuddin Informasi pribadiLahirNoormiliyani21 April 1959 (umur 64)Banjarmasin, Kalimantan Selatan, IndonesiaKebangsaan[IndonesiaPartai poli...

Félix MoreauxBiographieNaissance 9 mars 1828ReimsDécès 13 juin 1890 (à 62 ans)8e arrondissement de ParisNationalité françaiseFormation École nationale supérieure d'arts et métiersActivité IngénieurAutres informationsDistinction Chevalier de la Légion d'honneurmodifier - modifier le code - modifier Wikidata Pierre-Félix Moreaux est né à Reims, le 9 mars 1828, et mort à Paris 8e le 13 juin 1890. Ingénieur, ancien élève de l'École des arts et métiers (Châlons-sur-Ma...

Éphémérides Plan de Montréal en 1725Chronologie du Canada 1722 1723 1724 1725 1726 1727 1728Décennies au Canada :1690 1700 1710 1720 1730 1740 1750 Chronologie dans le monde 1722 1723 1724 1725 1726 1727 1728Décennies :1690 1700 1710 1720 1730 1740 1750Siècles :XVIe XVIIe XVIIIe XIXe XXeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure,...

Drémil-Lafage Le village vu du quartier de Montauriol en 2021. Blason Administration Pays France Région Occitanie Département Haute-Garonne Arrondissement Toulouse Intercommunalité Toulouse Métropole Maire Mandat Ida Russo 2020-2026 Code postal 31280 Code commune 31163 Démographie Gentilé Drémilois Populationmunicipale 2 638 hab. (2021 ) Densité 211 hab./km2 Géographie Coordonnées 43° 35′ 52″ nord, 1° 36′ 09″ est Altitude Min....

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

American medical doctor and skeptic (1945–2023) Harriet A. HallHall speaking in 2016Birth nameHarriet Anne Hoag[1]Born(1945-07-02)July 2, 1945St. Louis, Missouri, U.S.DiedJanuary 11, 2023(2023-01-11) (aged 77)Puyallup, Washington, U.S.Allegiance United StatesService/branch United States Air ForceYears of service1969–1989RankColonelAwardsMeritorious Service MedalAlma materUniversity of WashingtonSpouse(s)Kirk HallChildren2Other workMedical blogger and criti...

Boundary around the ancient city of Rome For the musical group, see Pomerium (early music group). Map of Rome in the time of the Roman Republic. The pomerium at that time is marked in pink; the Capitoline and Aventine are extra pomerium, 'beyond the wall', with their boundaries in yellow. The pomerium or pomoerium was a religious boundary around the city of Rome and cities controlled by Rome. In legal terms, Rome existed only within its pomerium; everything beyond it was simply territory (age...

Japanese medical scientist (1863–1930) Yamagiwa Katsusaburō山極 勝三郎Yamagiwa KatsusaburōBorn(1863-02-23)23 February 1863Ueda, Shinano Province (now Nagano Prefecture), JapanDied2 March 1930(1930-03-02) (aged 67)Tokyo, JapanNationalityJapaneseAlma materTokyo Imperial UniversityKnown forChemical carcinogenesisAwardsJapan Academy Prize, 1919Scientific careerFieldsPathologyInstitutionsTokyo Imperial University In this Japanese name, the surname is Yamagiwa. Yamagiwa Kats...

Questa voce o sezione sull'argomento centri abitati della Lombardia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Casale Cremasco-Vidolascocomune Casale Cremasco-Vidolasco – Veduta LocalizzazioneStato Italia Regione Lombardia Provincia Cremona AmministrazioneSindacoAntonio Giuseppe Grassi...

Former home stadium of Shrewsbury Town F.C. (1910-2007) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (February 2010) (Learn how and when to remove this message) Gay MeadowCrowd at the Gay Meadow on 25 February 2006Full nameGay MeadowLocationAbbey ForegateShrewsburySY2 6ABCapacity8,000 (3,639 seated)Field size114 x 74 yardsConstructionBuilt1910Opened1910Clos...

American football player and coach (born 1981) Not to be confused with Gerald Parker or Gerard Parker. Gerad ParkerCurrent positionTitleHead coachTeamTroyConferenceSun BeltRecord0–0Biographical detailsBorn (1981-01-04) January 4, 1981 (age 43)[1]Huntington, West Virginia, U.S.Playing career2000–2004Kentucky Position(s)Wide receiverCoaching career (HC unless noted)2005–2006Raceland-Worthington HS (KY) (WR/DB)2007Kentucky (GA)2008–2010UT Martin (PGC/RC)2011–2012Marshall (...

Frederick Law Olmsted Frederick Law OlmstedInformación personalNacimiento 26 de abril de 1822Island, Nueva York Fallecimiento 28 de agosto de 1903 (81 años)Belmont, Massachusetts Sepultura Old North Cemetery Nacionalidad EstadounidenseFamiliaPadres John Olmsted Charlotte Law Olmsted Cónyuge Mary Clevelands PerkinsHijos Charles Olsmetd y Frederick Law Olmsted Jr.EducaciónEducado en Phillips Academy Información profesionalÁrea arquitecto, botánico autodidactaSeudónimo Yeoman Obras notab...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Meezaan JafriJafri pada tahun 2019Lahir9 Mei 1995 (umur 29)Mumbai, Maharashtra, IndiaKebangsaanIndiaNama lainSyed Meezaan Ahmed JaffreyPekerjaanAktorAsisten sutradaraTahun aktif2019–sekarangDikenal atasHungama 2, Yaariyan 2Orang tuaJa...
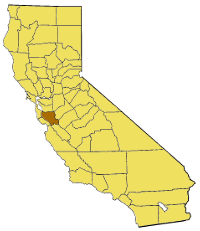
Silicon Valley Santa Clara County is generally considered to be the center of Silicon Valley.[1] Part of a series onLiving spaces MainHouse (detached) • Apartment • Housing projects • Human outpost • Tenement • Condominium • Mixed-use development (live-work) • Hotel • Hostel (travellers' hotel) • Castles • Public housing • Squat • Flophouse • Green home • Shack • Slum • Shanty town IssuesAffordability • Executive housing • Environmental planning •...

تعنك آثار من الطين النضيج من قرية تعنك في متحف إسطنبول الأثري الاسم الرسمي تعنك الإحداثيات 32°31′11″N 35°13′16″E / 32.519725°N 35.221058333333°E / 32.519725; 35.221058333333 تقسيم إداري البلد دولة فلسطين[1] التقسيم الأعلى محافظة جنين معلومات أخرى منطقة زمنية ت ع م+02:00، &...

Location in Rome Juan de Letrán redirects here. For other uses, see San Juan de Letrán (disambiguation). Late Baroque façade of the Archbasilica of Saint John Lateran, completed after a competition for the design by Alessandro Galilei in 1735 View showing Archbasilica and Palace Basilica and Palace - side view Lateran and Laterano are the shared names of several buildings in Rome. The properties were once owned by the Lateranus family of the Roman Empire. The Laterani lost their properties...





























