Nørre Højrup Sogn
| |||||||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini perlu dikembangkan dari artikel terkait di Wikipedia bahasa Inggris. (Juli 2023) klik [tampil] untuk melihat petunjuk sebelum menerjemahkan. Lihat versi terjemahan mesin dari artikel bahasa Inggris. Terjemahan mesin Google adalah titik awal yang berguna untuk terjemahan, tapi penerjemah harus merevisi kesalahan yang diperlukan dan meyakinkan bahwa hasil terjemahan tersebut akurat, bukan hanya salin-tempel teks hasil terjemahan mesin ke dalam Wikipedia bahasa Indonesia. Jangan...

Grafik Biaya Marginal Biaya marginal adalah peningkatan biaya total yang berasal dari produksi satu unit output produksi. Jika perusahaan memproduksi 1.000 unit, biaya tambahan peningkatan output menjadi 1.001 unit adalah biaya marginal. Biaya marginal mengukur biaya input tambahan yang diperlukan untuk memproduksi tiap unit output berikutnya. Karena biaya tetap tidak berubah ketika ada biaya output, biaya marginal mencerminkan perubahan biaya variabel. Jika fungsi biaya terdiferensiasi, biay...
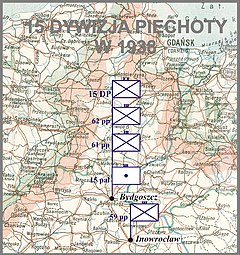
15th Greater Poland Infantry Division (Polish: 15 Wielkopolska Dywizja Piechoty) was a unit of the Polish Army in the interbellum period. Founded on February 17, 1920, and based on the 2nd Greater Poland Rifles Division, it actively participated in the Polish-Soviet War, including the Kiev offensive (1920), and the Battle of Warsaw. After Polish victory, the Division pushed the Red Army out of northern Mazovia. It then fought in the Battle of the Niemen River. 15th Infantry Division in 1938 D...

Artikel ini hampir seluruhnya merupakan ringkasan alur. Artikel ini harus diperluas untuk menyediakan cakupan konteks dunia nyata yang lebih seimbang. Please edit the article to focus on discussing the work rather than merely reiterating the plot. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Tali Pocong PerawanSutradaraArie AzisProduserYoen K, Ody Mulya HidayatDitulis olehAviv ElhamPemeranDewi PersikIbnu JamilRamon Y. TungkaDwi PutrantiwiZora VidyanataCatherine WilsonEn...

Diskografi Stray KidsStray Kids pada Desember 2019Album studio2Album kompilasi2Album video1Video musik54Extended play8Singel17Reissues1Soundtrack appearances2 Boy grup yang berbasis di Korea Selatan Stray Kids telah merilis dua album studio, dua album kompilasi, satu rilis ulang, delapan album mini, dan tujuh belas singel. Album Album Studio List of studio albums, with selected details, chart positions, sales and certifications Title Details Peak chart positions Sales Certifications KOR[1...

Un F-100D Super Sabre de l'US Air Force utilisant un système ZLTO. Le « zero-length launch system », ou « zero-length take-off system » (abrégé en ZLL, ZLTO, ZEL, ZELL), en français : « système de lancement zéro distance », était un système dans lequel un chasseur à réaction devait être placé sur une fusée installée sur une plateforme de lancement mobile. La plupart des expérimentations de ce système prirent place au cours des anné...

Voce principale: Düsseldorfer Turn- und Sportverein Fortuna 1895. Düsseldorfer Turn- und Sportverein Fortuna 1895Stagione 1988-1989Sport calcio Squadra Fortuna Düsseldorf Allenatore Aleksandar Ristić 2. Bundesliga1º posto Coppa di GermaniaPrimo turno Maggiori presenzeCampionato: Demandt (38)Totale: Demandt (39) Miglior marcatoreCampionato: Demandt (35)Totale: Demandt (35) StadioRheinstadion Maggior numero di spettatori22 000 vs. Meppen Minor numero di spettatori3 500 vs. ...

Volkswagen Beetle adalah simbol rekonstruksi Jerman Barat. Yang ada di gambar ini merupakan mobil ke-1.000.000. Wirtschaftswunder (Jerman: [ˈvɪʁt.ʃaftsˌvʊndɐ] ⓘ, keajaiban ekonomi), juga dikenal sebagai Keajaiban di Sungai Rhine, adalah istilah yang menjelaskan rekonstruksi dan perkembangan ekonomi Jerman Barat dan Austria yang begitu cepat setelah Perang Dunia II.[1][2] Istilah ini digunakan pertama kali oleh The Times tahun 1950.[butuh rujukan] Hal i...

Peta Saint-Maurice-sur-Moselle. Saint-Maurice-sur-Moselle merupakan sebuah komune di departemen Vosges yang terletak pada sebelah timur laut Prancis. Lihat pula Komune di departemen Vosges Referensi INSEE lbsKomune di departemen Vosges Les Ableuvenettes Ahéville Aingeville Ainvelle Allarmont Ambacourt Ameuvelle Anglemont Anould Aouze Arches Archettes Aroffe Arrentès-de-Corcieux Attignéville Attigny Aulnois Aumontzey Autigny-la-Tour Autreville Autrey Auzainvilliers Avillers Avrainville Avra...

Study of algorithms using numerical approximation Babylonian clay tablet YBC 7289 (c. 1800–1600 BCE) with annotations. The approximation of the square root of 2 is four sexagesimal figures, which is about six decimal figures. 1 + 24/60 + 51/602 + 10/603 = 1.41421296...[1] Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is th...

Town in Estonia This article is about the town with this name. For the administrative unit, see Haapsalu (urban municipality). Town in Lääne, EstoniaHaapsaluTownView from Haapsalu CastleHaapsaluLocation within Baltic Sea regionShow map of Baltic SeaHaapsaluLocation within EuropeShow map of EuropeHaapsaluLocation within EstoniaShow map of EstoniaCoordinates: 58°56′22″N 23°32′27″E / 58.93944°N 23.54083°E / 58.93944; 23.54083Country EstoniaCounty Lään...

Untuk pengertian lain, lihat Glenmore. 8°18′41″S 114°02′51″E / 8.3114°S 114.0474°E / -8.3114; 114.0474 Glenmore Kecamatan GlenmoreKecamatanPemerintah Kecamatan GlenmoreProvinsiJawa TimurKabupatenBanyuwangiKantor CamatJl. Raya Jember, Karangharjo, Glenmore, BanyuwangiPemerintahan • CamatDidik SuharsonoLuas[1] • Total368,89 km2 (14,243 sq mi)Ketinggian[1]372 m (1,220 ft)Populasi (2017)[...

Parthenaise Région d’origine Région Poitou en France Caractéristiques Taille Moyenne Robe Unie fauve-froment Autre Diffusion Régionale Utilisation Bouchère modifier La Parthenaise est une race bovine française originaire de la région de Parthenay, dans les Deux-Sèvres. Elle se caractérise par une robe fauve-froment unie et des muqueuses noires. C'était la troisième race française quant aux effectifs lors de la création de son livre généalogique en 1893. Les effectifs o...

Cet article est une ébauche concernant les Kiribati. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Les armoiries des Kiribati reprennent le blason dessiné par Sir Arthur Grimble en 1932 pour la colonie britannique des îles Gilbert et Ellice. La principale modification, intervenue en juillet 1979 lors de l'accession à l'indépendance des Kiribati est l'adjonction de la nouvelle devise nationale en gilbertin...

Practice of predicting information about a person's life Fortune teller redirects here. For the form of origami, see Paper fortune teller. For other uses, see Fortune teller (disambiguation). Gypsy Fortune-Teller (1841) by Taras Shevchenko Part of a series on theParanormal Main articles Astral projection Astrology Aura Bilocation Breatharianism Clairvoyance Close encounter Cold spot Crystal gazing Conjuration Cryptozoology Demonic possession Demonology Ectoplasm Electronic voice phenomenon Ex...

1989 film by Phil Alden Robinson For other uses, see Field of Dreams (disambiguation). Field of DreamsTheatrical release posterDirected byPhil Alden RobinsonScreenplay byPhil Alden RobinsonBased onShoeless Joeby W.P. KinsellaProduced by Lawrence Gordon Charles Gordon Starring Kevin Costner Amy Madigan James Earl Jones Ray Liotta Burt Lancaster CinematographyJohn LindleyEdited byIan CraffordMusic byJames HornerProductioncompanyGordon CompanyDistributed by Universal Pictures (United States) Car...

1492 decree expelling Jews from Spain A service in a Spanish synagogue, from the Sister Haggadah (c. 1350). The Alhambra Decree would bring Spanish Jewish life to a sudden end. The Alhambra Decree (also known as the Edict of Expulsion; Spanish: Decreto de la Alhambra, Edicto de Granada) was an edict issued on 31 March 1492, by the joint Catholic Monarchs of Spain (Isabella I of Castile and Ferdinand II of Aragon) ordering the expulsion of practising Jews from the Crowns of Castile and Aragon ...

Functional programming language This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Refal – news · newspapers · books · scholar · JSTOR (August 2020) (Learn how and when to remove this message) RefalParadigmPattern-matching and term-rewritingDesigned byValentin TurchinDeveloperValentin Turchin, S. Florentsev, V. Olyunin, et al.First appeared1968&#...

12th-century crusade For the Venetian-led attack on Constantinople in 1204, see Fourth Crusade. Venetian CrusadePart of the CrusadesSiege of Tyre by the Crusaders and the Venetian fleetDate1122–24LocationLevantResult Crusader victoryTerritorialchanges Tyre captured by JerusalemBelligerents Republic of VeniceKingdom of JerusalemCounty of Tripoli Fatimid CaliphateSeljuk EmpireCommanders and leaders Domenico MicheleWilliam I of BuresPons of Tripoli Toghtekin vteCrusadesIdeology and institution...
Property of a planar object which maps onto itself after rotation by any angle This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (February 2017) (Learn how and when to remove this message) In 2-dimensions an archery target has circular symmetry. A surface of revolution has circular symmetry around an axis in 3-dimensions. In ge...

