Zásobníkový automat
|
Read other articles:

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

Virus mosaik tembakau Tobacco mosaic virus Satu unit monomer dari Virus Mosaik TembakauKomposisi genom virus ICTVpositive-sense single-stranded RNA virus (en), positive-sense single-stranded RNA virus (en) dan positive-sense single-stranded RNA virus (en) TaksonomiSuperdomainBiotaDomainVirusFamiliVirgaviridaeGenusTobamovirusSpesiesTobacco mosaic virus lbs Virus mosaik tembakau (bahasa Inggris: Tobacco mosaic virus, sering disingkat TMV) adalah virus yang menyebabkan penyakit pada tembakau dan...

Painting by Antoine Watteau You can help expand this article with text translated from the corresponding article in French. (July 2018) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated tex...

Bupati Lampung UtaraLambang Kabupaten Lampung UtaraPetahanaBudi Utomosejak 3 November 2020KediamanPendapa Kabupaten Lampung UtaraMasa jabatan5 tahunDibentuk1946Pejabat pertamaBurhanudinSitus weblampungutarakab.go.id Berikut ini adalah Daftar Bupati Lampung Utara dari masa ke masa.[1] No Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Wakil Bupati 1 Burhanudin 1946 1947 1 2 Akhmad Akuan 1947 1950 2 3 H.Zainal Abidin Pagaralam 1950 1950 3 4 R.Sarikun tidak diketahui tidak diketahui 4 ...

Jubing (kanan) saat duet dengan Reda Jubing Kristianto (lahir 9 April 1966) adalah seorang gitaris fingerstyle Indonesia yang banyak menjelajahi berbagai repertoar. Jubing menggunakan gitar klasik sebagai instrumennya. Jubing dikenal pandai menghadirkan suasana yang ingin disampaikan sebuah lagu melalui gabungan berbagai teknik permainan gitar yang dinamis.[1] Selain itu, gitaris Indonesia ini juga memberikan sumbangan dalam musikalisasi puisi dengan melakukan kolaborasi antara permai...

Arudji Kartawinata Ketua Dewan Perwakilan Rakyat Ke-3Masa jabatan26 Januari 1963 – 24 Februari 1966PresidenSoekarno PendahuluZainul ArifinPenggantiMursalin Daeng Mamangung Informasi pribadiLahir(1905-05-05)5 Mei 1905Garut, Jawa Barat, Hindia BelandaMeninggal13 Juli 1970(1970-07-13) (umur 65)Jakarta, IndonesiaSuami/istriSumarsih Subiyati alias Yati Arudji.Sunting kotak info • L • B Arudji Kartawinata (5 Mei 1905 – 13 Juli 1970) adalah salah sat...

John Roselli (a destra) con Frank DeSimone John Roselli, nato come Filippo Sacco e soprannominato Handsome Johnny (Esperia, 4 luglio 1905 – Miami, 9 agosto 1976), è stato un mafioso italiano naturalizzato statunitense, membro di alto rango nella Chicago Outfit, nonché suo rappresentante a Las Vegas e Los Angeles. Indice 1 Biografia 1.1 Primi anni 1.2 Anni '40 1.3 Anni '50 1.4 Anni '60 1.5 Anni '70 2 Morte 3 Voci correlate 4 Altri progetti 5 Collegamenti esterni Biografia Primi anni Filipp...

Wakil Wali Kota PasuruanPetahanaAdi Wibowo, S.T.P., M.Si.sejak 26 Februari 2021Masa jabatan5 tahunDibentuk2005Pejabat pertamaPudjo BasukiSitus webSitus Resmi Kota Pasuruan Wakil Wali Kota Pasuruan adalah posisi kedua yang memerintah Kota Pasuruan di bawah Wali Kota Pasuruan. Posisi ini pertama kali dibentuk pada tahun 2005. Daftar No. Wakil Wali Kota Awal menjabat Akhir menjabat Prd. Ket. Wali Kota 1 Pudjo Basuki 2005 2010 Aminurokhman 2 Setiyono 18 Oktober 2010 18 Oktober 2015 H. Hasani...

Questa voce o sezione sull'argomento competizioni calcistiche non è ancora formattata secondo gli standard. Commento: Molte pagine di campionati regionali come queste vanno corrette con il nuovo modello di voce perché questa pagina è stata realizzata con modelli vecchi ed è obsoleta.In questa pagina sono da correggere:le squadre partecipanti, con la tabellina in cui non è più possibile linkare le squadre non enciclopediche alle città, la città va scritta nella riga inferiore con...

Questa voce sull'argomento calciatori italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Dionigi Corsi Nazionalità Italia Altezza 171 cm Peso 73 kg Calcio Ruolo Attaccante Carriera Squadre di club1 1913-1915 Hellas42 (33)1916-1917 Milan0 (0)1920-1922 Milan12 (4)192? Padova? (?) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il s...

Questa voce sugli argomenti stati scomparsi e Colombia è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Questa voce sull'argomento Panama è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Repubblica della Nuova Granada Motto: Libertad y Orden Repubblica della Nuova Granada - Localizzazione Dati amministrativiNome ufficialeRepública de la Nueva Granada Lingue uffic...

Questa voce sull'argomento contee dell'Iowa è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di JasperconteaLocalizzazioneStato Stati Uniti Stato federato Iowa AmministrazioneCapoluogoNewton Data di istituzione1846 TerritorioCoordinatedel capoluogo41°41′17″N 93°03′41″W / 41.688056°N 93.061389°W41.688056; -93.061389 (Contea di Jasper)Coordinate: 41°41′17″N 93°03′41″W / 41.688056°N...

LST-1108 at Rongerik Atoll on 8 March 1946, while assisting in the evacuation of Bikini Atoll's indigenous population ahead of Operation Crossroads. History United States NameUSS LST-1108 Laid down16 December 1944 Launched1 February 1945 Commissioned27 February 1945 Decommissioned15 August 1946 Fate Sold, 10 January 1948 Stricken25 September 1946 Argentina NameARA Cabo San Sebastian (BDT-11) Acquired1948 Out of service1966 General characteristics Class and typeLST-542-class LST Displacement ...

Sports history This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (August 2021) The history of black players in North American ice hockey has roots dating back to the late 19th century. The first black ice hockey star was Herb Carnegie during the Great Depression. Willie O'Ree broke the NHL's black color barrier with the Boston Bruins in 1958.[NB ...

Questa voce sull'argomento cestisti argentini è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Andrea AlomoNazionalità Argentina Pallacanestro CarrieraNazionale 1989-1999 Argentina Palmarès Campionati sudamericani BronzoCile 1989 Il simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manuale Andrea Laura Alomo (Buenos Aires, 6 marzo 1969) è un'ex cesti...

Cet article est une ébauche concernant le Maroc, le Sahara occidental et un groupe ethnique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. TeknaⵜⴰⴽⵏⴰتاكنةHabitat et aire de nomadisation des TeknaInformations généralesNom arabe TāknaÉchelon Confédération tribaleGéographieRégion principale Guelmim-Oued NounProvince principale Province de GuelmimProvince secondaire Province de Tan-TanChef-...
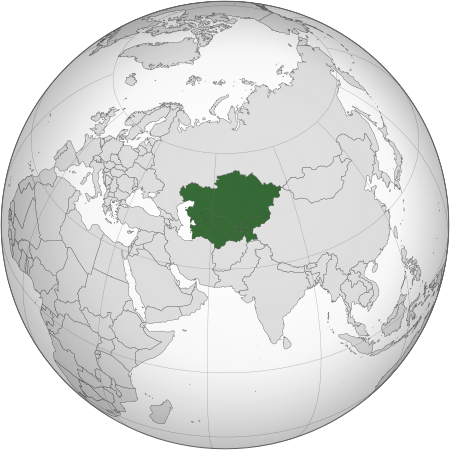
Subregion in Asia Not to be confused with Soviet Central Asia. Central AsiaArea4,003,451 km2 (1,545,741 sq mi)Population75,897,577 (2021) (16th)[1][2]Population density17.43/km2 (45.1/sq mi)GDP (PPP)$1.25 trillion (2023)[3]GDP (nominal)$446 billion (2023)[3]GDP per capita$5,900 (2023; nominal)[3]$16,400 (2023; PPP)[3]HDI0.779 (high)DemonymCentral AsianCountries 5 recognized Kazakhstan Kyrgyzstan Tajikistan &...

Street in Hong Kong Wan Chai Road in August 2006. Marker of the historical coastline in Wan Chai Road in March 2008. Wan Chai Road (灣仔道) is a main road in Wan Chai, on the north side of Hong Kong Island. Wan Chai Road is a L-shape road which was constructed in 1851 along Morrison Hill from the foot of Hospital Hill (now near the old Wan Chai Market building) to the beach at Observation Point (now near Tin Lok Lane). The road offers access, via Cross Lane, to Wan Chai Park (灣仔公園)...

Former government of New Zealand The Second Stafford Ministry was the eighth responsible government to be formed in New Zealand, and one of the longer-lasting ministries during this period. It formed in October 1865 and lasted until June 1869. However, it was defeated in a vote of confidence on 15 August 1866 and resigned, to be reconstituted with three ministers replaced, so some contemporaries regarded it as two separate Ministries. As the office of Premier had yet to be formally establishe...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) لمعانٍ أخرى، طالع الفرس (توضيح). الفرس - قرية - تقسيم إداري البلد اليمن المحافظة محاف...

