Přirozené číslo
|
Read other articles:

KuningasjätkäSutradaraTimo KoivusaloProduserTimo KoivusaloDitulis olehTimo KoivusaloJuha NumminenPemeranTapio LiinojaMartti SuosaloHeikki NousiainenPertti KoivulaAri WirtaPenata musikTimo KoivusaloJaakko SaloSinematograferTimo HeinänenPertti MutanenPenyuntingTimo KoivusaloJyrki LuukkoPerusahaanproduksiArtista FilmiDistributorBuena Vista Home EntertainmentTanggal rilis19 Februari 1999Durasi102 menitNegara FinlandiaBahasaFinlandia Kulkuri ja joutsen (Indonesia: Gelandangan dan angsacod...

Lambang Chili Lambang Chili diadopsi pada 26 Juni 1834 dan dibuat oleh seniman Inggris Charles Wood Taylor (1792-1856). Lambang ini terdiri dari sebuah perisai yang dibagi menjadi dua bagian: bagian atas yang berwarna biru dan bawah yang berwarna merah. Sebuah bintang putih bersudut lima ditempatkan di tengah perisai. Lambang ini ditopang oleh burung kondor di bagian kanan dan huemul di bagian kirinya. Kedua hewan itu mengenakan mahkota angkatan laut untuk melambangkan heroisme Angkatan Laut ...

Vous lisez un « bon article » labellisé en 2008. Pour les articles homonymes, voir Dartmouth. Dartmouth CollegeLe Dartmouth Hall.HistoireFondation 13 décembre 1769StatutType Université privée (en)Nom officiel Dartmouth CollegeRégime linguistique AnglaisFondateur Eleazar WheelockMembre de Réseau Matariki (en), Ivy League, ORCID (d)Site web (en) www.dartmouth.eduChiffres-clésÉtudiants 6 761 (2021)Effectif 3 961 (2020)LocalisationPays États-UnisLocalisation H...

Artikel ini bukan mengenai Honda Sonic 150R. Sonic X Seri animeSutradaraHajime KamegakiStudioTokyo Movie ShinshaPelisensiNA 4Kids Entertainment (2003–2012)Saban Brands (2012–2014)Saluranasli Indosiar (Oktober 2004-Mei 2006), Spacetoon Kids Station, TV Tokyo Jetix The CW Television Network (The CW4Kids), Fox Broadcasting Company (hingga 2008), Disney XD (sejak tahun 2009), Syfy (mulai tanggal 16 Februari 2011) YTV Jetix, TF1 Channel Seven RTÉ Two, Jetix, Jetix, Jetix Russia TVB Jade, Star...

Frase murid yang Yesus kasihi (Yunani: ὁ μαθητὴς ὃν ἠγάπα ὁ Ἰησοῦς, ho mathētēs hon ēgapā ho Iēsous) atau, dalam Yohanes 20:2, murid yang dikasihi Yesus (Yunani: ὃν ἐφίλει ὁ Ἰησοῦς, hon efilei ho Iēsous) disebutkan enam kali dalam Injil Yohanes,[1] namun tidak dalam kitab-kitab Perjanjian Baru lainnya. Yohanes 21:24 menyatakan bahwa Injil Yohanes mendasarkan pada pernyataan tertulis dari murid ini. Sejak akhir abad ke-1, m...

Questa voce sull'argomento calciatori tunisini è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Khaled Fadhel Nazionalità Tunisia Altezza 182 cm Peso 80 kg Calcio Ruolo Portiere Termine carriera 2008 Carriera Squadre di club1 1996-2001 Club Africain? (-?)2001-2004 Sfaxien? (-?)2004-2005 Diyarbakırspor26 (-?)2005-2007 K. Erciyesspor45 (-?)2007-2008 Monastir? (-?) Nazional...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Rajendra Prasad – berita · surat kabar · buku · cendekiawan · JSTOR Dr. Rajendra Prasadडा. राजेन्द्र प्रसाद Presiden India PertamaMasa jabatanJanuari 1950 – 1...

Election for the 39th Parliament of Australia 1998 Australian federal election ← 1996 3 October 1998 (1998-10-03)[a] 2001 → ← outgoing memberselected members →All 148 seats in the House of Representatives75 seats were needed for a majority in the House40 (of the 76) seats in the SenateRegistered12,154,050 3.52%Turnout11,545,201 (94.99%)(0.78 pp) First party Second party Leader John Howard Kim Beazley Party Libera...

Step-grandson of George Washington (1781–1857) George Washington Parke CustisSalt print of Custis, circa 1856BornApril 30, 1781Rosaryville, Maryland, U.S.DiedOctober 10, 1857(1857-10-10) (aged 76)Arlington House, Arlington, Virginia, U.S.Resting placeArlington National CemeteryEducationGermantown AcademyPrinceton UniversitySt John's CollegeOccupationAuthorSpouse Mary Lee Fitzhugh (m. 1804)Children5 or 6, including Maria and MaryParentsJohn Parke CustisEle...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Style of lighthouse architecture This article is about the style of lighthouse architecture. For the American house design, see Cape Cod (house). The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (December 2021) (Learn how and when to remove this message) This article needs additional citations for verification. Please help improve this artic...

Навчально-науковий інститут інноваційних освітніх технологій Західноукраїнського національного університету Герб навчально-наукового інституту інноваційних освітніх технологій ЗУНУ Скорочена назва ННІІОТ ЗУНУ Основні дані Засновано 2013 Заклад Західноукраїнський �...

تحوي هذه المقالة أو هذا القسم ترجمة آلية. فضلًا، ساهم في تدقيقها وتحسينها أو إزالتها لأنها تخالف سياسات ويكيبيديا. (نقاش) (يوليو 2016) جغرافيا لاتفيامعلومات عامةالبلد لاتفيا القارة أوروبا الساحل بحر البلطيق الحدود بيلاروسإستونياليتوانياروسياالسويدبولنداالاتحاد السوفيتي �...

Study of evolutionary relationships between organisms This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Phylogenetics – news · newspapers · books · scholar · JSTOR (February 2024) (Learn how and when to remove this message) Part of a series onEvolutionary biologyDarwin's finches by John Gould Index Introductio...

Residential community with controlled entrances and often a closed perimeter of walls/fences Not to be confused with Closed city. This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2022) (Learn how and when to remove this message) Entrance to the Paradise Village Grand Marina Villas, Nuevo Vallarta, Nayarit, Mexico A gated community (or walled communit...

Tank tempur utama M1 Abrams Angkatan Darat Amerika Serikat, dengan peningkatan TUSK (perisai komposit, reaktif, dan serpihan). Perisai kendaraan, atau disebut juga perisai tempur, umumnya digunakan pada kendaraan militer dengan tujuan menahan dampak berbagai serpihan pecahan peluru, peluru, peluru artileri, roket dan rudal terhadap personil militer yang berlindung di dalam kendaraan ketika terjadi serangan musuh. Berbagai kendaraan tempur lapis baja yang memiliki perisai antara lain adalah ta...

Pour les articles homonymes, voir Terrell. Mary Church TerrellBiographieNaissance 23 septembre 1863MemphisDécès 24 juillet 1954 (à 90 ans)AnnapolisSépulture Lincoln Memorial Cemetery de Suitland (Maryland)Nom de naissance Mary Eliza ChurchNationalité américaineFormation 1884 : Bachelor of Arts / licence (Oberlin College) 1888 : Master of Arts / master (Oberlin College)Activités Écrivaine, femme politique, suffragiste, militante pour les droits des femmes, militante des...
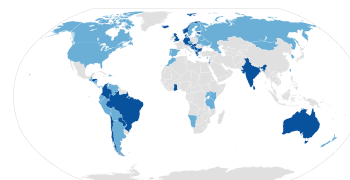
國際民主聯盟International Democrat Union国际民主联盟所屬政黨執政的國家分布(深蓝色)截至2021年2月 (2021-02)[update]簡稱IDU成立時間1983年總部 德国慕尼黑服务地区全球會員73官方語言英語主席 史蒂芬·哈珀(保守黨)副主席 Brian Loughnane(英语:Brian Loughnane)(自由黨)目標世界各地中間偏右至右派政黨和組織的聯盟網站idu.org 系列条目保守主义 分支 激情保守主义�...

British naval commander and Tory politician The Right HonourableThe Earl of EgmontPortrait as a young naval officer, by George Francis JosephBorn14 March 1794Died2 August 1874(1874-08-02) (aged 80)AllegianceUnited KingdomService/branchRoyal NavyYears of service1805–1874RankAdmiralCommandsHMS InfernalHMS BritomartBattles/wars Napoleonic Wars Battle of Trafalgar Battle of Maguelone War of 1812 Battle of Hampden Bombardment of Algiers AwardsNaval General Service MedalSpouse(s)Jane Ho...

Mechanical component that converts rotational motion to reciprocal motion For the fictional characters of the same name, see Camshaft (Transformers). A camshaft operating two valves A camshaft is a shaft that contains a row of pointed cams in order to convert rotational motion to reciprocating motion. Camshafts are used in piston engines (to operate the intake and exhaust valves),[1][2] mechanically controlled ignition systems and early electric motor speed controllers. Camsha...




































