Ordinální aritmetika
|
Read other articles:

This is a list of notable naval frogman and may contain combat units, salvage units, training units and diving research units which are present or past commands of any branch of the armed forces of any country. Algeria Navy Special Action Regiment (RASM) – Special forces regiment of the Algerian naval forces. Argentina Tactical Divers Group (Buzos Tácticos) is the special operations unit of the Argentine navy. The operatives are combat divers, EOD/demolition technicians, and parachut...

Lake in Massachusetts, United States of America Houghton's PondHoughton's PondHoughton's PondShow map of MassachusettsHoughton's PondShow map of the United StatesLocationMilton, MassachusettsCoordinates42°12′26″N 71°5′44″W / 42.20722°N 71.09556°W / 42.20722; -71.09556TypeGlacial PondBasin countriesUnited StatesSurface area24 acres (97,000 m2)Max. depth42 ft (13 m) Houghton's Pond is a spring-fed kettle hole pond in Milton, Massachusetts,...

1991 single by Tevin CampbellJust Ask Me ToSingle by Tevin Campbellfrom the album T.E.V.I.N. and Boyz n the Hood Soundtrack B-sideHip Hop MixReleasedJune 26, 1991Recorded1991GenreNew jack swing[1]Length4:07LabelQwest/Warner Bros.Songwriter(s)Al B. Sure, Kyle WestProducer(s)Al B. Sure, Kyle WestTevin Campbell singles chronology Round and Round (1990) Just Ask Me To (1991) Tell Me What You Want Me to Do (1991) Just Ask Me To is a song by American R&B Singer Tevin Campbell. It was r...
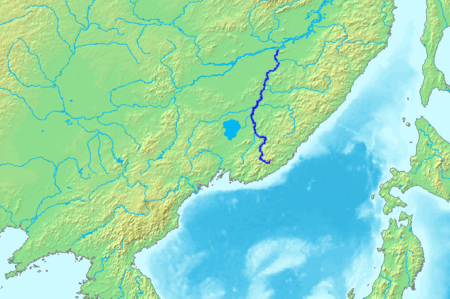
Konflik perbatasan Tiongkok-Soviet di pulau darmanskyBagian dari Perang Dinginkegagalan soviet dalam menghancurkan tank T-62 dan mundurnya pasukan soviet dari pulau zhenbaoTanggal1969LokasiPerbatasan antara Tiongkok dengan Uni SovietHasil kemenangan china,china mengontrol pulau darmansky secara de factoPerubahanwilayah Perselisihan akhirnya diselesaikan dalam serangkaian perjanjian perbatasan yang dibuat oleh Rusia dan Cina pada tahun 1991, 1994 dan 2004, sebagai akibatnya Cina menerima beber...

Untuk kegunaan lain, lihat Kumbang kotoran (disambiguasi). Kumbang kotoran Scarabaeus viettei (syn. Madateuchus viettei, Scarabaeidae) di hutan berduri kering dekat dengan Mangily, Madagaskar barat Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insekta Ordo: Coleoptera Subordo: Polyphaga Superfamili: Scarabaeoidea (sebagian) Famili: Scarabaeidae Kumbang kotoran merupakan kumbang jenis kumbang yang sebagian atau seluruhnya memgonsumsi kotoran. Kumbang kotoran dapat mengubur kot...

Old Mutual plcJenisPerusahaan publikKode emitenLSE: OMLJSE: OMLTemplat:Zimbabwe Stock ExchangeIndustriJasa keuanganDidirikan17 May 1845 (Cape Town, Cape Colony)KantorpusatLondon, InggrisTokohkunciPatrick O'Sullivan, Chairman Julian Roberts, CEOProdukAsuransi jiwaTabungan dan investasiManajemen asetPerbankanAsuransi jangka pendekPendapatan£15.478 juta (2014)[1]Laba operasi£1.364 juta (2014)[1]Laba bersih£852 juta(2014)[1]Karyawan56.812 (2015)[2]...

Cet article est une ébauche concernant la mode et le vêtement. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Un ensemble de couvertures en « polaire ». Les textiles dits polaires sont des textiles synthétiques isolants constitués de polytéréphtalate d'éthylène (PET) et d'autres fibres synthétiques, caractérisé (comme le velours) par une « pilosité importante cachant la structure t...

Digital media company This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Spinlet – news · newspapers · books · scholar · JSTOR (May 2016) (Learn how and when ...

Parish in Louisiana, United States Parish in LouisianaLivingston ParishParishLivingston Parish Courthouse in LivingstonLocation within the U.S. state of LouisianaLouisiana's location within the U.S.Coordinates: 30°26′N 90°44′W / 30.44°N 90.73°W / 30.44; -90.73Country United StatesState LouisianaFoundedFebruary 10, 1832Named forEdward LivingstonSeatLivingstonLargest cityDenham SpringsArea • Total703 sq mi (1,820 km2) •...

فينيكس سيتي الاسم الرسمي (بالإنجليزية: Phenix City) الإحداثيات 32°28′22″N 85°01′12″W / 32.472777777778°N 85.02°W / 32.472777777778; -85.02 [1] تاريخ التأسيس 23 فبراير 1883 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة روسيل[4]مقاطعة لي[4...

Battle between the Roman and Gallic empires For the battle in 451, see Battle of the Catalaunian Plains. 48°57′27″N 4°21′54″E / 48.9575°N 4.365°E / 48.9575; 4.365 Battle of ChâlonsPart of the Crisis of the Third CenturyChâlonsBattle of Châlons (274) (France)DateFebruary or March 274 CE (0274-02-22)LocationChâlons-en-Champagne, FranceResult Roman victory End of the Gallic Empire. Reunification of the Roman Empire.Belligerents Roman Empire Gallic Emp...

Proto-Germanic word for Roman or Romanized peoples Brass replica of the Tjurkö bracteate showing the word ᚹᚨᛚᚺᚨᚲᚢᚱᚾᛖ walhakurne ('Roman grain', i.e. gold coin) *Walhaz is a reconstructed Proto-Germanic word meaning 'foreigner',[1][2] or more specifically 'Roman', 'Romance-speaker' or '(romanized) Celt', and survives in the English words of 'Wales/Welsh'[1][3] and 'Cornwall.'[4] The term was used by the ancient Germanic peoples to de...

Temperate rainforest in the Appalachian Mountains This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may lack focus or may be about more than one topic. Please help improve this article, possibly by splitting the article and/or by introducing a disambiguation page, or discuss this issue on the talk page. (June 2024) This article's factual accuracy is disputed. Relevant discussio...

Untuk tempat lain yang bernama sama, lihat Villemer. Peta infrastruktur dan tata guna lahan di Komune Villemer. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungai VillemerNegaraPrancisArondisemenFontainebleauKantonMoret-sur-LoingAntarkomuneCommunauté de communes Moret Seine et LoingPemerintahan • Wali kota (2008-2014) Alain Houdry • Populasi1...

Battle during the Seven Years' War Battle of BurkersdorfPart of the Third Silesian War (Seven Years' War)Date21 July 1762LocationBurkersdorf, present-day Poland50°47′35″N 16°27′58″E / 50.793056°N 16.466111°E / 50.793056; 16.466111Result Prusso-Russian victoryBelligerents Prussia Russia AustriaCommanders and leaders Frederick the Great Leopold Joseph von DaunStrength 23,000[1] 20,000[1]Casualties and losses 1,600 killed or wounded[1...

Silica pseudomorph after gypsum crystals and silicified serpulid polychaete tubes Pseudomorph of goethite after pyrite In mineralogy, a pseudomorph is a mineral or mineral compound that appears in an atypical form (crystal system), resulting from a substitution process in which the appearance and dimensions remain constant, but the original mineral is replaced by another. The name literally means false form. Terminology for pseudomorphs is replacer after original, as in brookite after rutile....

世界跆拳道聯盟World Taekwondo簡稱WT成立時間1973年5月28日類型國際體育組織總部 韩国首爾江南區三成洞官方語言韓語 英語隸屬國際奧林匹克委員會主席 趙正源[1]目標武術和運動網站www.worldtaekwondo.org 世界跆拳道聯盟(英語:World Taekwondo,縮寫:WT),是世界跆拳道管理機構,亦為國際奧林匹克委員會的其中之一,負責安排跆拳道的國際性賽事。現任主席為趙正源(�...

Town in Alberta, CanadaMorinvilleTownTown of MorinvilleThe Provincial Building in downtown Morinville Coat of armsLogoMotto(s): We Listen, We Serve, We AchieveMorinvilleLocation in Sturgeon CountyShow map of Sturgeon CountyMorinvilleLocation in AlbertaShow map of AlbertaCoordinates: 53°48′08″N 113°38′59″W / 53.80222°N 113.64972°W / 53.80222; -113.64972CountryCanadaProvinceAlbertaRegionEdmonton Metropolitan RegionCensus division11Municipal districtSturg...

1956 film by Ken Hughes The Brain MachineTheatrical release posterDirected byKen HughesWritten byKen HughesProduced byAlec C. SnowdenStarringMaxwell ReedElizabeth AllanPatrick BarrRussell NapierCinematographyJosef AmborEdited byGeoffrey MullerMusic byRichard TaylorProductioncompanyMerton Park StudiosDistributed byAnglo-AmalgamatedRelease date February 1956 (1956-02) (US)[1] Running time84 minutesCountryUnited KingdomLanguageEnglish The Brain Machine is a 1956 British thr...

German Commander-in-Chief during World War II (1881–1948) Walther von BrauchitschBrauchitsch in 1939Commander-in-Chief of the German ArmyIn office4 February 1938 – 19 December 1941ChancellorAdolf HitlerPreceded byWerner von FritschSucceeded byAdolf Hitler Personal detailsBornWalther Heinrich Alfred Hermann von Brauchitsch(1881-10-04)4 October 1881Berlin, Prussia, German EmpireDied18 October 1948(1948-10-18) (aged 67)Hamburg, British-occupied GermanyResting placeSalzgitterSpo...






















![{\displaystyle \{[0,0],[0,1],[0,2]\}\cup \{[1,0],[1,1]\}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6527c5ff1e81c590b0d304a795576299c0ec7f0a)
![{\displaystyle \{[0,0],[0,1],[0,2],[1,0],[1,1]\}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4b9fdd5088a40e3518502879f5b86abf680b2e8)




![{\displaystyle \{[0,0]\}\cup \{[1,0],[1,1],[1,2],[1,3],...\}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5bb221e7f4752a99cdd21b74c1e8a48b2ab2de7)
![{\displaystyle \{[0,0],[1,0],[1,1],[1,2],[1,3],...\}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbe7f50c245d0fc1ef68cfd70c6e996b9c4b9607)




![{\displaystyle \{[0,0],[0,1],[0,2],[1,0],[1,1],[1,2]\}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/465e189015493d658baefd07f74ee70f0fa47a63)


![{\displaystyle \{[0,0],[0,1],[1,0],[1,1],[2,0],...\}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e4556f8976bf190296beb3f8c824963b2fd7be6)

![{\displaystyle \{[0,0],[0,1],[0,2],...,[1,0],[1,1],[1,2],...\}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db9ef2ab55b1396099eae117a55d17317c48b907)
































