Funkce alef
|
Read other articles:

Halaman ini berisi artikel tentang seri televisi. Untuk novel dalam seri A Song of Ice and Fire, lihat A Game of Thrones. Untuk kegunaan lain, lihat Game of Thrones (disambiguasi). Game of Thrones (waralaba) beralih ke halaman ini. Untuk seri buku, lihat A Song of Ice and Fire. Game of ThronesGenre Fantasi Drama seri Pembuat David Benioff D. B. Weiss BerdasarkanA Song of Ice and Fireoleh George R. R. MartinPemeranlihat daftar karakter Game of ThronesPenggubah lagu temaRamin DjawadiLagu pembuk...

Untuk kegunaan lain, lihat Lost Highway. Lost HighwayAlbum studio karya Bon JoviDirilis8 Juni 2007 (2007-06-08)(see Release history)DirekamNashville, Los AngelesGenreHard rock, country rockDurasi49:50LabelIsland / Mercury NashvilleProduserDann Huff John Shanks Desmond Child (Executive Producer)Kronologi Bon Jovi Have A Nice Day (2005)Have A Nice Day2005 Lost Highway (2007) The Circle (2009)The Circle 2009 Templat:Extra album cover 2 Singel dalam album Lost Highway (You Want to) Make ...

Annual English women's football (soccer) award 2023 winner Rachel Daly The Professional Footballers' Association Women's Players' Player of the Year is an annual award given to the player who is voted to have been the best of the year in English women's football.[1] The award has been presented since the 2012–13 season[2] and the winner is chosen by a vote amongst the members of the players' trade union, the Professional Footballers' Association (PFA). The current holder is ...

Untuk tokoh Alkitab yang menjadi nama dari kitab ini, lihat Ezra dan Nehemia. Untuk perbedaan penyusunan dan penamaan pada kitab-kitab terkait, lihat Esdras. Untuk kegunaan lain, lihat Ezra (disambiguasi) dan Nehemia (disambiguasi). Alkitab IbraniTanakhYosua 1:1 pada Kodeks Aleppo Taurat (Pengajaran)KejadianBeresyitKeluaranSyemotImamatWaiyiqraBilanganBemidbarUlanganDevarim Nevi'im (Nabi-nabi) Awal YosuaYehosyuaHakim-hakimSyofetimSamuelSyemu'elRaja-rajaMelakhim Akhir YesayaYesyayah...

Перуанский анчоус Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые �...

Swediah Army regiment I 13 redirects here. For other uses, see I-13 (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dalarna Regiment – news · newspapers · books · scholar · JSTOR (March 2013) (Learn how and when to remove this message) Dalarna RegimentDalregementetActive1625–1709, 1710–...

1 آنة هندية وجه العملة: تمثال نصفي لملك جورج السادس, مع كتابة نصية جورج السادس الملك الإمبراطور. ظهر العملة: سنة الضرب والقيمة العددية الاسمية بالإنجليزية، الأردية، البنغالية، تيلغو و الديفاناغاري. 125,548,000 عملة سكت في الفترة من (1938 إلى 1940) طابع بريدي للدولة القعيطية بقيمة آن�...

У этого термина существуют и другие значения, см. Тур. Запрос «Bos taurus primigenius» перенаправляется сюда; см. также другие значения. † Тур Скелет тура Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:В...

Голубянки Самец голубянки икар Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ПервичноротыеБез ранга:ЛиняющиеБез ранга:PanarthropodaТип:ЧленистоногиеПодтип:ТрахейнодышащиеНадкласс:ШестиногиеКласс...

Department in ArgentinaSan Isidro Partido de San IsidroDepartment Coat of armsLogolocation of San Isidro Partido in Gran Buenos AiresCoordinates: 34°28′S 58°30′W / 34.467°S 58.500°W / -34.467; -58.500CountryArgentinaEstablished1784Founded byDomingo de AcassusoSeatSan IsidroGovernment • MayorGustavo Posse (Partido Vecinal - JxC)Area • Total51.44 km2 (19.86 sq mi)Population[1] • Total291,608 • ...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Romanian football club This article is about the football team. For the women's handball team, see CSM Cetate Devatrans Deva. Football clubCSM DevaFull nameClub SportivMunicipal DevaNickname(s)Devenii(The People of Deva)Cetățenii(The Citizens)Short nameCSM DevaFounded1921; 103 years ago (1921)as Mureșul Deva1994; 30 years ago (1994)as Vega Deva2003; 21 years ago (2003)as CS Deva2006; 18 years ago (2006)as Mureșul Deva...

Japanese anime television series This article is about the 2011 animated television series. For its 2018 sequel, see Steins;Gate 0 (TV series). Steins;GateCover art for the UK home media release, featuring the main castGenrePsychological thriller[1][2]Science fiction[3] Anime television seriesDirected byHiroshi HamasakiTakuya SatōTomoki Kobayashi (OVA)Produced byKenjirō GomiTakayuki MatsunagaYoshito DannoShinsaku TanakaKozue KananiwaYoshinao DoiWritten ...

José León Suárez Localidad José León SuárezLocalización de José León Suárez en Región Metropolitana de Buenos AiresCoordenadas 34°31′45″S 58°34′24″O / -34.5292, -58.5733Idioma oficial españolEntidad Localidad • País Argentina • Provincia Buenos Aires • Partido General San MartínIntendente Fernando Moreira (PJ-UP)Eventos históricos • Fundación 10 de mayo de 1932Altitud • Media 19 m s. n. m.Po...

Shakta poet of eighteenth century Bengal Ramprasad SenBornc. 1723[1] or c. 1718[2]Garalgachha, Hooghly District, Bengal SubahDied1781(1781-00-00) (aged 62–63)[2]Halisahar, Bengal Presidency, British IndiaOther namesSadhak RamprasadOccupation(s)Saint, poetKnown forRamprasadi Part of a series onShaktism History Deities Mahadevi (Supreme) Devi Shakti Parvati Durga Mahavidya Kali Lalita Matrikas Lakshmi Saraswati Scriptures and texts Vedas Tantras Yogini S...

У Вікіпедії є статті про інших людей із прізвищем Гуржій.Гуржій Андрій МиколайовичНародився 14 грудня 1946(1946-12-14) (77 років)ІванівкаКраїна СРСР УкраїнаДіяльність науковець, викладач університетуAlma mater Київський політехнічний інститут (1969)Галузь інформаційні техно�...

56th NBA season This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 2001–02 NBA season – news · newspapers · books · scholar · JSTOR (December 2022) Sports season2001–02 NBA seasonLeagueNational Basketball AssociationSportBasketballDurationOctober 30, 2001 – April 17, 2002April 20 – June 2, 200...
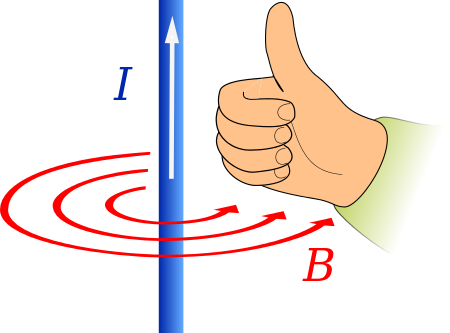
Applied to electromagnetism Chirality with hands and two enantiomers of a generic amino acid The direction of current flow and induced magnetic flux follow a handness relationship The term chiral /ˈkaɪrəl/ describes an object, especially a molecule, which has or produces a non-superposable mirror image of itself. In chemistry, such a molecule is called an enantiomer or is said to exhibit chirality or enantiomerism. The term chiral comes from the Greek word for the human hand, which itself ...

موجيلوف علم شعار الاسم الرسمي (بالبيلاروسية: Магілёў) الإحداثيات 53°54′32″N 30°20′35″E / 53.90894°N 30.34296°E / 53.90894; 30.34296 [1] تقسيم إداري البلد بيلاروس (25 أغسطس 1991–)[2][3] التقسيم الأعلى موغيليوف أوبلاست (15 يناير 1938–) عاصمة لـ موغيليوف...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Mario Bermejo Bermejo (2009)Informasi pribadiNama lengkap Mario Bermejo CastanedoTanggal lahir 7 Oktober 1978 (umur 45)Tempat lahir Santander, SpanyolTinggi 178 m (584 ft 0 in)Posisi bermain StrikerKarier junior Racing SantanderKar...






















