Sistema cristal·lí
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Gimpo 김포Municipal CityTranskripsi Korea • Hangul김포시 • Hanja金浦市 • Revised RomanizationGimpo-si • McCune-ReischauerKimp'o-si Emblem GimpoNegara Korea SelatanRegionSudogwonPembagian administratif1 eup, 5 myeon, 4 dongLuas • Total276,6 km2 (1,068 sq mi)Populasi • Total203.391 • Kepadatan735,3/km2 (19,040/sq mi) • DialekSeoul Gimpo adalah kota yang terletak ...

CaerphillyNegara asalWalesSumber susuSapiDipasteurisasiTidakTeksturKerasWaktu pematangan10 minggu[1] Caerphilly adalah keju dari Wales yang menggunakan susu sapi mentah dalam proses pembuatannya.[1] Keju Caerphilly memiliki tingkat kelembapan yang lebih tinggi dibandingkan dengan keju tradisional Inggris lainnya.[1] Keju ini pertama kali dibuat di daerah Caerphilly di Wales pada tahun 1830.[1][2] Keju ini direndam dalam air asin semalaman sehingga menye...

Kadaroesman Jaksa Agung Republik Indonesia ke-6Masa jabatan1962–1964PresidenSoekarnoWakilSetia Untung ArimuladiSunarta PendahuluR. GoenawanPenggantiPetahana Informasi pribadiMeninggal9 Desember 1992MakamTaman Makam Pahlawan Nasional Utama KalibataKebangsaanIndonesiaProfesiJaksaSunting kotak info • L • B R. Kadaroesman, S.H. adalah Jaksa Agung Republik Indonesia untuk periode 1962 sampai 1964.[1] Kadaroesman wafat pada tanggal 9 Desember 1992 dan dimakamkan di Taman...

Jamaican dancehall singer MavadoMavado in 2008Background informationBirth nameDavid Constantine Brooks[1]Also known asGully GodBorn (1981-11-30) 30 November 1981 (age 42)[1]Kingston, Jamaica[1]GenresDancehallreggaeOccupation(s)SingerdeejayYears active2004–presentLabelsWe the BestCash MoneyMansion RecordsVPMusical artist David Constantine Brooks (born 30 November 1981),[1] better known by his stage name Mavado, is a Jamaican dancehall singer. Mavado signe...

Regency in South Sulawesi, IndonesiaPangkajene & Islands Regency Kabupaten Pangkajene dan KepulauanRegency Coat of armsLocation within South SulawesiPangkajene & Islands RegencyShow map of SulawesiPangkajene & Islands RegencyShow map of IndonesiaCoordinates: 4°45′S 119°30′E / 4.750°S 119.500°E / -4.750; 119.500Country IndonesiaProvince South SulawesiCapitalPangkajeneArea • Total1,112.29 km2 (429.46 sq mi)Population (m...

MontroseInformasi latar belakangAsalAmerika SerikatGenreHard rockTahun aktif1973–1977, 1987, 2005LabelWarner Bros.Artis terkaitVan Halen, Chickenfoot, Edgar Winter Group, Van Morrison, Buster Brown, Gamma, ScorpionsMantan anggotaRonnie Montrose - gitarSammy Hagar - vokalBill Church - bassDenny Carmassi - drumSteve Smith - drumAlan Fitzgerald - bassBob James - vokalJim Alcivar - keyboardRandy Jo Hobbs - bassGlenn Letsch - bassJohnny Edwards - vokalJames Kottak - drum Montrose adalah band har...

Questa voce sugli argomenti allenatori di pallacanestro statunitensi e cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti dei progetti di riferimento 1, 2. Jack Sikma Jack Sikma in azione con la maglia di IWU Nazionalità Stati Uniti Altezza 211 cm Peso 104 kg Pallacanestro Ruolo CentroAllenatore Termine carriera 1991 - giocatore2018 - allenatore Hall of fame Naismith Hall of Fame (2019) Carriera Giov...

Australian athlete and Governor of South Australia The HonourableMarjorie Jackson-NelsonAC CVO MBE DStJMarjorie Jackson-Nelson in 200733rd Governor of South AustraliaIn office3 November 2001 – 8 August 2007MonarchElizabeth IIPremierRob Kerin (2001–02)Mike Rann (2002–07)Preceded bySir Eric NealSucceeded byKevin Scarce Personal detailsBorn (1931-09-13) 13 September 1931 (age 92)Coffs Harbour, New South Wales, AustraliaSpouse Peter Nelson &#...

Fictional character from EastEnders Soap opera character Ravi GulatiEastEnders characterPortrayed byAaron ThiaraDuration2022–presentFirst appearanceEpisode 65154 July 2022 (2022-07-04)ClassificationPresent; regularIntroduced byChris ClenshawIn-universe informationOccupationDrug dealer Career criminalRestauranteurBusinessmanFatherNish PanesarMotherHaspira GulatiAdoptive fatherRanveer GulatiStepmotherSuki Panesar Nina Gupta (adoptive)Half-brothers Kheerat Pa...

Nampan putar di restoran tiongkok Nampan putar adalah sarana makan putar ( baki berputar) yang diletakkan di atas meja untuk membantu pendistribusian makanan . Nampan putar dapat dibuat dari berbagai bahan tetapi biasanya terbuat dari kaca, kayu, atau plastik . Mereka berbentuk lingkaran dan ditempatkan di tengah meja untuk berbagi hidangan dengan mudah di antara pengunjung. Meskipun hal ini umum dijumpai di restoran tiongkok, penemu nampan putar bukanlah penemuan orang Cina-Amerika.[1 ...
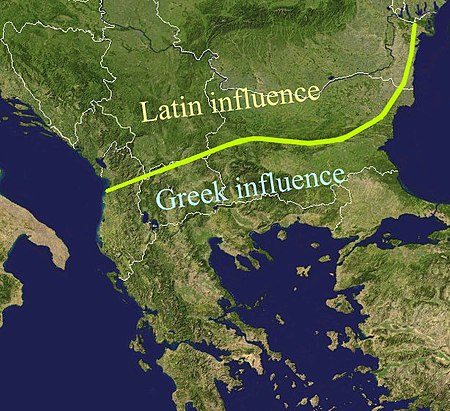
Peta wilayah dan perbatasan bahasa Bali, Jawa, Madura, Melayu (Betawi), dan Sunda di pulau Jawa dan sekitarnya. Garis perbatasan dan pengaruh bahasa Yunani dan Latin di Balkan. Perbatasan bahasa adalah garis semu yang memisahkan dua wilayah bahasa. Istilah ini umumnya dimaksudkan untuk menyiratkan kurangnya kesalingpahaman antara kedua bahasa. Jika dua bahasa atau dialek yang berdekatan dapat dimengerti satu sama lain, tidak ada batas tegas yang berkembang, karena kedua bahasa dapat terus ber...

Mountain range in the US states of Texas and New Mexico For the smaller range in the southwest New Mexico Bootheel, see Guadalupe Mountains (Hidalgo County). For the mountain range in Extremadura, Spain, see Sierra de Villuercas. Guadalupe MountainsGuadalupe MountainsHighest pointPeakGuadalupe PeakElevation8,751 ft (2,667 m)Coordinates31°53′28″N 104°51′36″W / 31.89111°N 104.86000°W / 31.89111; -104.86000DimensionsLength65 mi (105 km...

Extinct family of mammals BisonalveusTemporal range: 60–56 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Early to Middle Tiffanian Mandibula of Bisonalveus browni Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: †Cimolesta Family: †Pantolestidae Subfamily: †Pentacodontinae Genus: †Bisonalveus Species B. browni (Gazin, 1956) B. holtzmani (Gingerich, 1983) Bisonalveus is an extinct genus of shrew-like[1] mammals that were ...
American political commentator (born 1976) This article is about the American political commentator and Youtube personality. For the author, see David Rubin (author). For other uses, see David Rubin. Dave RubinBornDavid Joshua Rubin (1976-06-26) June 26, 1976 (age 47)New York City, U.S.EducationBinghamton University (BA)Occupation(s)Talk show host, blogger, radio personality, television personality, YouTube personalityYears active1998–presentKnown forThe Rubin ReportPolitical...

American magazine and media organization Psychology TodayCover of the magazine's January 2023 issueEditor-in-chiefKaja PerinaCategoriesPsychologyFrequencyBimonthlyPublisherJohn Thomas[1]Total circulation275,000 (as of 2023[update])[2]Founded1967; 57 years ago (1967)CompanySussex PublishersCountryUnited StatesBased in16 West 22nd Street, Suite 200, New York City, U.S.LanguageEnglishWebsitepsychologytoday.comISSN0033-3107 Psychology Today is an American...

American politically progressive monthly magazine For other things called In These Times, see In These Times. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: In These Times publication – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and when to remove this message) In These Times...

العلاقات اليابانية الصربية اليابان صربيا اليابان صربيا تعديل مصدري - تعديل العلاقات اليابانية الصربية هي العلاقات الثنائية التي تجمع بين اليابان وصربيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة الي�...

2011 British filmKill KeithDirected byAndy ThompsonWritten byPete BensonTim MajorAndy ThompsonProduced byPaul AthertonChristian JamesTim MajorAndy ThompsonStarringSusannah FieldingMarc PickeringDavid EasterKeith ChegwinJoe TraciniCinematographyLuke BryantEdited byRichard ColtonMusic byJohn ZealeyProductioncompaniesDead on Arrival DigitalGaia MediaRelease date 11 November 2011 (2011-11-11) [1]Running time93 minutes[1]CountryUnited KingdomLanguageEnglish Kill Kei...

圖一 直线AB与直线CD垂直,因为它们相交所构成的两个角(分别以橙色和蓝色表示)相等。 垂直是一个几何术语。在平面几何中,如果一条直线与另一条直线相交,且它们构成的任意相邻两个角相等,那么这两条直线相互垂直。术语“垂直”(符號:⊥)衍生一个形容词(垂直)或者名词(垂线)。因此,根据圖一,直线AB通过B点与直线CD相互垂直。像图一这样,如果一条�...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...






















