Rosendale (Missouri)

Plantilla:Infotaula geografia políticaRosendale
Imatge
Tipusciutat dels Estats Units Modifica el valor a Wikidata
Localització
Modifica el valor a Wikidata Map
 40° 02′ 30″ N, 94° 49′ 19″ O / 40.0417°N,94.8219°O / 40.0417; -94.8219
EstatEstats Units d'Amèrica
Estat federatMissouri
Comtatcomtat d'Andrew Modifica el valor a Wikidata
Població humana
Població119 (2020) Modifica el valor a Wikidata (153,89 hab./km²)
Llars31 (2020) Modifica el valor a Wikidata
Geografia
Superfície0,773263 km² Modifica el valor a Wikidata
Aigua3,4909 % (1r abril 2010) Modifica el valor a Wikidata
Altitud278 m Modifica el valor a Wikidata
Creació1856 Modifica el valor a Wikidata
Identificador descriptiu
Codi postal64483 Modifica el valor a Wikidata
Prefix telefònic816 Modifica el valor a Wikidata

Rosendale és una població dels Estats Units a l'estat de Missouri. Segons el cens del 2000 tenia 180 habitants.[1]

Demografia

Segons el cens del 2000, Rosendale tenia 180 habitants, 69 habitatges, i 50 famílies.[2] La densitat de població era de 224,2 habitants per km².[3]

Dels 69 habitatges en un 37,7% hi vivien nens de menys de 18 anys, en un 52,2% hi vivien parelles casades, en un 15,9% dones solteres, i en un 27,5% no eren unitats familiars. En el 18,8% dels habitatges hi vivien persones soles el 5,8% de les quals corresponia a persones de 65 anys o més que vivien soles. El nombre mitjà de persones vivint en cada habitatge era de 2,61 i el nombre mitjà de persones que vivien en cada família era de 3,06.[2]

Per edats la població es repartia de la següent manera: un 30% tenia menys de 18 anys, un 9,4% entre 18 i 24, un 30,6% entre 25 i 44, un 18,3% de 45 a 60 i un 11,7% 65 anys o més.

L'edat mediana era de 31 anys. Per cada 100 dones de 18 o més anys hi havia 103,2 homes.[2]

La renda mediana per habitatge era de 26.731 $ i la renda mediana per família de 30.313 $. Els homes tenien una renda mediana de 25.179 $ mentre que les dones 18.750 $. La renda per capita de la població era de 12.847 $. Entorn del 10,2% de les famílies i l'11,9% de la població estaven per davall del llindar de pobresa.

Poblacions més properes

El següent diagrama mostra les poblacions més properes.

Distàncies i posició relativa d'algunes poblacions
Distàncies i posició relativa d'algunes poblacions
RosendaleRosendale
Població amb 257 habitants (2000)Barnard (15 km)
Població amb 234 habitants (2000)Bolckow (8 km)
Població amb 211 habitants (2000)Fillmore (13 km)
Població amb 87 habitants (2000)Guilford (16 km)
Població amb 56 habitants (2000)Rea (5 km)
Població amb 4762 habitants (2000)Savannah (11 km)

Referències

  1. ↑ «U.S. Gazetteer: 2000 and 1990». Oficina del Cens dels Estats Units, 10-07-2008.
  2. ↑ 2,0 2,1 2,2 «Fact Sheet- Rosendale». American Fact Finder. Oficina del Cens dels Estats Units, 12-01-2010. Arxivat de l'original el 2020-02-10. [Consulta: 8 agost 2010].
  3. ↑ «Geographic Comparison Table- Rosendale». American Fact Finder. Oficina del Cens dels Estats Units, 12-01-2010. Arxivat de l'original el 2010-08-20. [Consulta: 8 agost 2010].

Read other articles:

Girl's Talk

Girl's TalkSampul Versi CAlbum studio karya KaraDirilis24 November 2010 (JPN)6 Februari 2011 (PHL)[1]Direkam2010GenrePop, dance-popDurasi35:26 (Standard)45:46 (Limited Editions C)BahasaJepangLabelUniversal SigmaKronologi Kara Jumping(2010)Jumping2010 Girl's Talk(2010) Step(2011)Step2011 Singel dalam album Girl's Talk MisterDirilis: 11 Agustus 2010 JumpingDirilis: 10 November 2010 Girl's Talk (ガールズトークcode: ja is deprecated , Gāruzu Tōku) adalah album studio berb...

 

 

Agustiar Sabran

Agustiar Sabran Anggota Dewan Perwakilan RakyatPetahanaMulai menjabat 1 Oktober 2019Daerah pemilihanKalimantan Tengah Informasi pribadiLahir17 Agustus 1972 (umur 51)Sampit, Kalimantan Tengah, IndonesiaPartai politikPDI-PSuami/istriThisia Halijam ​(m. 2021)​KerabatSugianto Sabran (adik)Sunting kotak info • L • B H. Agustiar Sabran, S.Kom. (lahir 17 Agustus 1972) adalah seorang politikus Indonesia. Saat ini ia menjabat sebagai Anggota DPR-RI s...

 

 

Abbas (politikus)

AbbasAbbas sebagai Wabup Kolut 2017-2022 Wakil Bupati Kolaka Utara Ke-3PetahanaMulai menjabat 22 Agustus 2017PresidenJoko WidodoGubernurAli MaziBupatiNur Rahman Umar PendahuluBoby AlimuddinPenggantiPetahanaWakil Ketua DPRD Kabupaten Kolaka UtaraMasa jabatan2009–2014Anggota DPRD Kabupaten Kolaka UtaraMasa jabatan2014–2016Masa jabatan2009–2014 Informasi pribadiLahirAbbas05 Januari 1968 (umur 56)BonePartai politikPKBSuami/istriHj. SukmawatiAnak2Alma mater Unhas (1996)ProfesiPo...

CIBC Bank USA

American banking division of CIBC This article is about the United States subsidiary. For the Canadian parent company, see Canadian Imperial Bank of Commerce. CIBC Bank USAFormerlyThe PrivateBank and Trust Company[1]Company typeSubsidiaryTraded asNasdaq: PVTB (1999–2017)IndustryFinancial servicesFounded1989Headquarters120 South LaSalle Street, Chicago, IllinoisProductsConsumer Banking, Corporate Banking, Insurance, Investment Banking, Mortgage loans, Private Banking, Private Eq...

 

 

Navajo County, Arizona

County in Arizona, United States County in ArizonaNavajo CountyCountyHistoric Navajo County Courthouse and Museum in Holbrook SealLocation within the U.S. state of ArizonaArizona's location within the U.S.Coordinates: 35°29′52″N 110°17′23″W / 35.4978°N 110.2897°W / 35.4978; -110.2897Country United StatesState ArizonaFoundedMarch 21, 1895Named forNavajo NationSeatHolbrookLargest cityShow LowArea • Total9,960 sq mi (25,800 ...

 

 

باول فان همست

باول فان همست (بالهولندية: Paul Van Himst)‏  معلومات شخصية الميلاد 2 أكتوبر 1943 (العمر 80 سنة) الطول 1.81 م (5 قدم 11 1⁄2 بوصة) مركز اللعب مهاجم الجنسية بلجيكا  مسيرة الشباب سنوات فريق 1951–1959 رويال أندرلخت المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1959–1975 رويال أندرلخت 457 (233) 197...

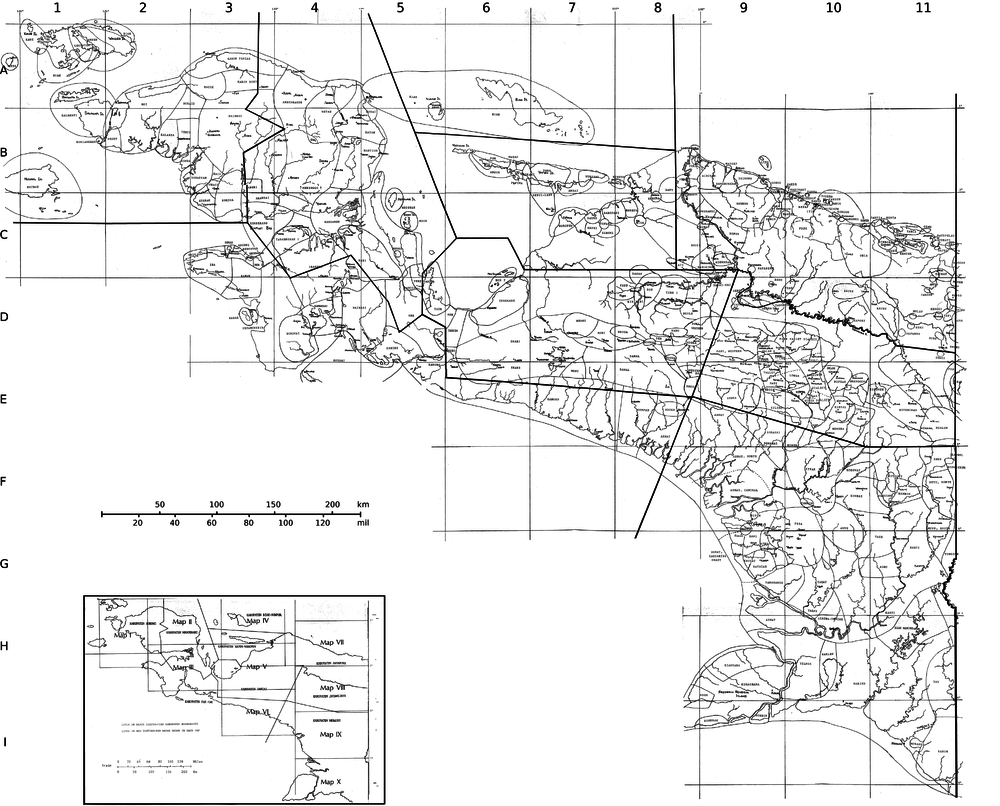
Daftar bahasa di Papua

Untuk bahasa di Papua Nugini, lihat Daftar bahasa di Papua Nugini. Halaman ini memuat daftar bahasa-bahasa di Papua. Daftar ini tidak dimaksudkan sebagai suatu daftar yang lengkap atau selalu terbarui. Jika Anda melihat artikel yang seharusnya tercantum di sini, silakan sunting halaman ini dan tambahkan pranala ke artikel tersebut. Gunakan perubahan terkait untuk melihat perubahan terbaru dari artikel-artikel yang tercantum pada halaman ini. Peta bahasa-bahasa di Papua dalam Index of Irian Ja...

 

 

Wincanton Classic 1993

Wincanton Classic 1993GénéralitésCourse 5e Wincanton ClassicCompétition Coupe du monde de cyclisme sur route 1993Date 15 août 1993Distance 231 kmPays  Royaume-UniLieu de départ LeedsLieu d'arrivée LeedsRésultatsVainqueur Alberto VolpiDeuxième Jesper SkibbyTroisième Maurizio FondriestWincanton Classic 1992Leeds International Classic 1994modifier - modifier le code - modifier Wikidata La 5e édition de la Wincanton Classic a lieu le 15 août 1993. Remportée par l'Italien Al...

 

 

Daniel Andersson

Daniel Andersson Daniel Andersson ketika masih bermainInformasi pribadiNama lengkap Daniel Jerry AnderssonTanggal lahir 28 Agustus 1977 (umur 46)Tempat lahir Lund, SwedenTinggi 1,78 m (5 ft 10 in)Posisi bermain Gelandang / BekInformasi klubKlub saat ini Malmö FF (Asisten manajer)Karier junior0000–1994 Bjärreds IFKarier senior*Tahun Tim Tampil (Gol)1995–1998 Malmö FF 85 (11)1998–2001 Bari 97 (16)2001–2002 Venezia 29 (0)2002–2004 Palermo 0 (0)2002–2003 → Ch...

Samsung Galaxy Mini

Samsung Galaxy Mini GT-S5570PembuatSamsung ElectronicsSeriGalaxyJaringanGSM 850 MHz/900 MHz/1800 MHz/1900 MHz HSDPA 7.2 Mbit/s 850 MHz / 900 MHz / 1700 MHz / 1900 MHz / 2100 MHzRilis pertamaFebruari 2011PendahuluSamsung Galaxy 5PenerusSamsung Galaxy Mini 2TipeSmartphoneFaktor bentukSlateDimensi1.104 mm (43,5 in) H606 mm (23,9 in) W121 mm (4,8 in) D[1]Berat1.066 g (37,6 oz)Sistem Op...

 

 

俄亥俄州

  「俄亥俄」重定向至此。关于其他用法，请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號：七葉果之州地图中高亮部分为俄亥俄州坐标：38°27'N－41°58'N, 80°32'W－84°49'W国家 美國加入聯邦1803年3月1日，在1953年8月7日追溯頒定（第17个加入联邦）首府哥倫布（及最大城市）政府 • 州长（英语：List of Governors of {{{Name}}}]]） •&...

 

 

Повітряні сили Збройних сил України

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Шифр простой замены

Принцип работы шифра Цезаря состоит в «сдвиге» букв на 3 позиции. Для расшифровки нужно произвести обратную операцию Принцип работы программы ROT13, которая не предназначена для защиты, но лишь для скрытия текста (например, потенциально оскорбительного). Для восстановлени�...

 

 

Pablo Alí

Military commander Pablo Alí Pablo Alí was a chief military commander of Haitian origin, who was in charge of the so-called Battalion 31 or Batallon de Morenos (Dark-skinned Battalion),[1] freed slaves which joined the ranks of the Dominican army. Alí directed the battalion to participate in the Italian rebellion of 1810, during the government of Sánchez Ramírez.[2] He was said to have been most prominent, achieving great military distinction in Santo Domingo.[3] ...

 

 

نوط الواجب العسكري (مصر)

نوط الواجب العسكريمعلومات عامةالبلد  مصر صورة شريط الخدمةتعديل - تعديل مصدري - تعديل ويكي بيانات الذهبي الفضي - الظهر الفضي - الوجه الشريط العسكري نوط الواجب العسكري المصري نوط الواجب العسكري أو (بالإنجليزية: The Medal of Military Duty)‏ هو نوط عسكري مصري أنشئ في 9 يوليو 1953، ويمنح للع...

Playboy Mansion

Halaman ini berisi artikel tentang rumah. Untuk lagu U2, lihat The Playboy Mansion (lagu). Untuk permainan video, lihat Playboy: The Mansion. Playboy Mansion WestPlayboy MansionLocation within Los Angeles Metropolitan AreaTampilkan peta Los Angeles Metropolitan AreaPlayboy MansionPlayboy Mansion (California)Tampilkan peta CaliforniaPlayboy MansionPlayboy Mansion (Amerika Serikat)Tampilkan peta Amerika SerikatInformasi umumJenisRumahGaya arsitekturGothic RevivalTudor RevivalLokasi10236 Charing...

 

 

Stasiun Kitsuki

Stasiun Kitsuki杵築駅Stasiun Kitsuki pada Februari 2009LokasiKitsuki, ŌitaJepangKoordinat33°24′40″N 131°34′32″E / 33.41111°N 131.57556°E / 33.41111; 131.57556Operator JR KyushuJalur■ Jalur Utama NippōLetak99.2 km dari KokuraJumlah peron1 peron samping + 1 peron pulauKonstruksiJenis strukturAtas tanahInformasi lainSitus webSitus web resmiSejarahDibuka22 Maret 1911 (1911-03-22)PenumpangFY2016758 per hariPeringkatke-195 (di antara stasiun-stasiun J...

 

 

York–Beverley line

Former English railway line York–Beverley lineStamford Bridge Viaduct and approaches (2008)OverviewStatusClosedLocaleYorkshireHistoryOpenedYork to Market Weighton, 1847Market Weighton to Beverley, 1865Closed1965TechnicalTrack length21.5 mi (34.6 km) York Mkt.Weighton11 mi (18 km) Mkt.Weighton BeverleyTrack gauge4 ft 8+1⁄2 in (1,435 mm) standard gauge vteYork–Beverley line Legend York–Scarborough lineto York & Scarborough Bootha...

Baron Manners

Barony in the Peerage of the United Kingdom Thomas Manners-Sutton, 1st Baron Manners Baron Manners, of Foston in the County of Lincoln,[1] is a title in the Peerage of the United Kingdom. It was created in 1807 for the lawyer and politician Sir Thomas Manners-Sutton. He served as Solicitor-General from 1802 to 1805 and as Lord Chancellor of Ireland from 1807 to 1827. Manners-Sutton was the fifth son of Lord George Manners-Sutton, third son of John Manners, 3rd Duke of Rutland. His eld...

 

 

Euler's sum of powers conjecture

Disproved conjecture in number theory In number theory, Euler's conjecture is a disproved conjecture related to Fermat's Last Theorem. It was proposed by Leonhard Euler in 1769. It states that for all integers n and k greater than 1, if the sum of n many kth powers of positive integers is itself a kth power, then n is greater than or equal to k: a 1 k + a 2 k + ⋯ + a n k = b k ⟹ n ≥ k {\displaystyle a_{1}^{k}+a_{2}^{k}+\dots +a_{n}^{k}=b^{k}\implies n\geq k} The conjectur...