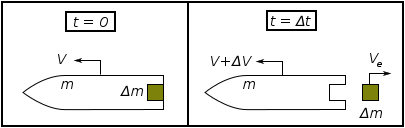Equació de Tsiolkovski
|
Read other articles:

Disambiguazione – Se stai cercando altri significati, vedi Éclair (disambigua). ÉclairÉclair al cioccolatoOriginiLuogo d'origine Francia DettagliCategoriadolce Ingredienti principalipasta choux, crema pasticcera, cioccolato o caffè, budino o panna montata Éclair al cioccolato e alla crema L’éclair (pron. [e'klɛʁ], eclèr; lampo, folgore) è un pasticcino lungo e sottile di origine francese a base di pasta choux, farcito di crema o cioccolato e glassato. Indice 1 Caratteristi...

Экономика Монголии Вид на деловой квартал Улан-Батора Валюта Монгольский тугрик Международныеорганизации ВТО[1][2] Статистика ВВП ▲ $18,78 млрд (2023) (номинальный)[3] Рост ВВП ▲ 5,5 % (2023)[3] ВВП на душу населения ▲ $5350 (2023) (номинальный)[3] ▲ $15 090 (2023) (ППС)[3]...

Christian revivals in Britain and the Thirteen Colonies in the 1730s and 1740s Jonathan Edwards' 1741 sermon Sinners in the Hands of an Angry God Great Awakenings in America First (c. 1730–1755) Second (c. 1790–1840) Third (c. 1855–1930) Fourth (c. 1960–1980) vte The First Great Awakening (sometimes Great Awakening) or the Evangelical Revival was a series of Christian revivals that swept Britain and its thirteen North American colonies in the 1730s and 1740s. T...

Bajing Ireng dan Jaka SembungSutradaraTjut DjalilProduserGope T. SamtaniSabirin KasdaniDitulis olehDjair WarniponakandaPemeranBarry PrimaAlex KalangiEl ManikGodfried SanchoPiet PagauRita ZaharaSyamsuddin SyafeiSyamsuri KaempuanTizar PurboZurmainiPenata musikGatot SudartoSinematograferThomas SusantoPenyuntingJanis BadarDistributorRapi FilmsTanggal rilisJanuari 1985Durasi94 menitNegara IndonesiaPrekuelSi Buta Lawan Jaka Sembung (1983)SekuelJaka Sembung dan Dewi Samudra (1990)IMDbInformasi...

فضيلة الشيخ محمد عجاج الخطيب معلومات شخصية الميلاد سنة 1932 دمشق الوفاة 11 أكتوبر 2021 (88–89 سنة) دمشق مواطنة الجمهورية السورية الثانية (1932–1958) الجمهورية العربية المتحدة (1958–1961) سوريا (1961–2021) الحياة العملية المدرسة الأم كلية الشريعة (–1959)كلية دار العلوم (�...

A 1787 portrait of Amos Simon Cottle by William Palmer Amos Simon Cottle (1766–1800) was an English translator and poet. His publications include, Icelandic poetry or The Edda of Sæmund which was first printed in 1797 with Robert Southey as a co-author.[1] Life The elder brother of the author Joseph Cottle, he was born in Gloucestershire. He received a classical education at Mr. Henderson's school at Hanham, near Bristol, and subsequently as a mature student at Magdalene College, ...

Jalan Tol Lingkar Luar Jakarta 2JORR 2Informasi ruteDikelola oleh : PT Jasa Marga (Persero) Tbk (Benda–Limo) PT Translingkar Kita Jaya (Limo–Cimanggis) PT Cimanggis Cibitung Tollways (Cimanggis-Cibitung) PT Cibitung Tanjung Priok Port Tollways (Cibitung-Cilincing) Panjang:110.4 km (68,6 mi)Berdiri:27 Januari 2012; 12 tahun lalu (2012-01-27) – sekarangPersimpangan besarOrbit sekitar wilayah urban JabodetabekUjung Barat: Bandar Udara Internasional Soekarno-Hatta Jalan ...

Halaman ini berisi artikel tentang neokonservatisme di Amerika Serikat. Untuk neokonservatisme di tempat lain, lihat Neokonservatisme (disambiguasi). Konservatisme modern beralih ke halaman ini. Untuk konservatisme modern di negara lain, lihat Konservatisme § Konservatisme modern di negara lain. Bagian dari seriKonservatisme Varian Budaya Fiskal Hijau Liberal Libertarian Nasional Neo- Kanan Baru Satu bangsa Paleo- Agama Sosial Tradisionalis Konsep Konformitas Tradisi Norma sosial Famili...

For other uses, see Clearcut (disambiguation). Forestry/logging practice in which most or all trees in an area are uniformly cut down After a century of clearcutting, this forest, near the source of the Lewis and Clark River in Clatsop County, Oregon, is a patchwork. In each patch, most of the trees are the same age. Clearcutting, clearfelling or clearcut logging is a forestry/logging practice in which most or all trees in an area are uniformly cut down. Along with shelterwood and seed tree h...

AirportTaranto-Grottaglie AirportAeroporto di Taranto-GrottaglieIATA: TARICAO: LIBGSummaryAirport typePublicServesTaranto / Grottaglie, ItalyElevation AMSL215 ft / 66 mCoordinates40°31′03″N 017°24′11″E / 40.51750°N 17.40306°E / 40.51750; 17.40306MapTarantoLocation of airport in ItalyRunways Direction Length Surface m ft 17/35 3,200 10,500 Asphalt Statistics (2022)Passengers1,083Passenger change 21-22 10.1%Aircraft movements913Movements change...

2013 song by Miley Cyrus featuring French Montana FUSong by Miley Cyrus featuring French Montanafrom the album Bangerz ReleasedSeptember 30, 2013Recorded2013Genre Dubstep EDM Length3:51LabelRCASongwriter(s)Rami Samir AfuniMaureen McDonaldKarim KharbouchMiley CyrusProducer(s)Afuni FU is a song by American singer Miley Cyrus, featuring American rapper French Montana for her fourth studio album, Bangerz (2013). It was written by Cyrus, Rami Samir Afuni, Montana, and MoZella. Production was helme...

Yo Gabba Gabba!Kartu judul Yo Gabba Gabba!GenreSerial televisi anak-anakPembuatChristian JacobsScott SchultzPengembangKay Wilson StallingsSutradara Christian Jacobs Scott Schultz Matt Fackrell Matt Chapman PemeranLance RobertsonPengisi suara Adam Delbert Christian Jacobs Emma Jacobs Briggs Amos Mossi Watene Erin Pearce Negara asalAmerika SerikatJmlh. musim4Jmlh. episode66 (daftar episode)ProduksiProduser eksekutifMichael Polis Jon BerrettProduserJustin LyonRita PeruggiDurasi25 menitRumah pro...

Rantai peluruhan dari timbal-212 sampai ke timbal-208, menunjukkan produk tengah peluruhan. Dalam fisika nuklir, produk peluruhan (juga dikenal sebagai produk turunan, isotop turunan atau nukleida turunan) adalah sisa nuklida yang tersisa dari peluruhan radioaktif. Peluruhan radioaktif sering terjadi melalui serangkaian langkah (rantai peluruhan). Misalnya, 238U meluruh ke 234Th yang meluruh ke 234mPa yang meluruh, dan seterusnya, ke 206Pb (yang stabil): U 238 ⟶ Th 234 ⏟ ⟶...

Law Enforcement Agency Law enforcement agency Louisiana State PolicePatch of Louisiana State PoliceBadge of Louisiana State PoliceAbbreviationLSPMottoCourtesy, Loyalty, Service!Agency overviewFormed1922; 102 years ago (1922)Preceding agencyLouisiana Highway CommissionEmployees1,548 (as of 2004)[1]Jurisdictional structureOperations jurisdictionLouisiana, USLSP Troop MapSize51,885 square miles (134,380 km2)Population4,468,976Legal jurisdiction StatewideGeneral nat...

Disambiguazione – Peru rimanda qui. Se stai cercando altri significati, vedi Peru (disambigua). Perù (dettagli) (dettagli) (ES) Firme y Feliz por la Unión(IT) Saldo e Felice per l'Unione Perù - Localizzazione Dati amministrativiNome completoRepubblica del Perù Nome ufficiale(ES) República del Perú(QU) Piruw Ripuwlika(AY) Piruw Suyu Lingue ufficialispagnolo, aymara e quechua Capitale Lima (9.822.514 ab. / 2017) PoliticaForma di governoRepubblica presidenzi...

Storia dell'alfabeto Media età del bronzo XIX secolo a.C. Ugaritico XV secolo a.C. Proto-cananeo XV secolo a.C. Fenicio XIV–XI secolo a.C. Paleo-ebraico X secolo a.C. Samaritano VI secolo a.C. Aramaico VIII secolo a.C. Brāhmī VI secolo a.C. Devanāgarī VIII secolo d.C. Tibetano VII secolo d.C. Khmer/giavanese IX secolo d.C. Ebraico III secolo a.C. Siriaco II secolo a.C. Arabo IV secolo d.C. Pahlavi III secolo a.C. Avestico IV secolo d.C. Kharoshthi III secolo a.C. Palmireno I secolo a....

Questa voce sull'argomento stagioni delle società calcistiche francesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Voce principale: Paris Saint-Germain Football Club. Paris Saint-Germain F.C.Stagione 2001-2002Sport calcio Squadra Paris Saint-Germain Allenatore Luis Fernández Division 14° Coppa di FranciaQuarti di finale Coupe de la LigueSemifinali Miglior marcatoreCampionato: Ronaldinho (9)Totale: Ronaldinho (13) StadioParco dei Principi 2...

Western Roman emperor from 461 to 465 Libius SeverusSolidus of Libius Severus marked:d·n· libius severus p·f· aug·Roman emperor in the West (unrecognized in the East) Reign19 November 461 – 14 November 465[nb 1]PredecessorMajorianSuccessorAnthemiusEastern emperorLeo IBornLucania[5]Died14 November 465[nb 1]NamesLibius Severus (Serpentius?)ReligionChristianity Libius Severus , sometimes enumerated as Severus III,[6][7][8][9] was Wes...

Soap opera character Pamela DouglasThe Bold and the Beautiful characterPortrayed byAlley MillsDuration 2006–2019 2021-2022 First appearanceDecember 1, 2006Last appearanceDecember 23, 2022ClassificationPast; guestCreated byBradley BellIn-universe informationOther namesLorraine DouglasOccupationReceptionistFatherJohn DouglasMotherAnn DouglasSistersStephanie ForresterNephewsRidge ForresterThorne ForresterNiecesAngela ForresterKristen ForresterFelicia ForresterOther rel...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目可参照英語維基百科相應條目来扩充。 (2019年10月26日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 此條目需要补充更多来源。 (2019年...