Demostració ontològica de Gödel
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. BvrtanAsalCimanggis, Depok, IndonesiaGenreBlack metalTahun aktif2011 (2011)–sekarangLabelLumbung Angker Records, Blackandje RecordsArtis terkaitGoatmaster, Vlaar, Proletar, SickmathSitus webSitus web resmiAnggota Nico Zul Levoy Mantan anggota Ab...

Atal Bihari VajpayeeBRVajpayee pada tahun 2002 Perdana Menteri India 10Masa jabatan19 Maret 1998 – 22 Mei 2004PresidenK. R. NarayananA. P. J. Abdul KalamWakilL. K. Advani PendahuluI. K. GujralPenggantiManmohan SinghMasa jabatan16 Mei 1996 – 1 Juni 1996PresidenShankar Dayal Sharma PendahuluP. V. Narasimha RaoPenggantiH. D. Deve GowdaMenteri Luar Negeri IndiaMasa jabatan26 Maret 1977 – 28 Juli 1979Perdana MenteriMorarji Desai PendahuluYashwantrao ChavanPengg...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Emma StoneStone pada tahun 2018LahirEmily Jean Stone6 November 1988 (umur 35)Scottsdale, Arizona, USAPekerjaanAktrisTahun aktif2004–sekarangTinggi168 cm (5 ft 6 in)PenghargaanDaftar penuhTanda tangan Emily Jean Emma Stone (lahir 6 November 1988) adalah aktris asal Amerika Serikat. Ia telah menerima banyak penghargaan, diantaranya satu Academy Award, satu BAFTA Award, dan satu Golden Globe Award, dan juga merupakan aktris dengan bayaran tertinggi di dunia pada tahun...

Ecumenical and religious flag used to represent Christianity. This article is about the Christian Flag adopted by the United States Federal Council of Churches. For use of various Christian flags since antiquity, see History of Christian flags. Christian FlagUseBanner AdoptedSeptember 26, 1897; 126 years ago (1897-09-26) (unofficial)January 23, 1942; 82 years ago (1942-01-23) (official)DesignA white banner with a red Latin Cross charged upon a blue cantonDe...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Türbe Gazi Husrev-beg (1480–1541) di Masjid Gazi Husrev-beg, Sarajevo Türbe (dalam bahasa Turki berarti makam) adalah istilah yang mengacu kepada mausoleum atau monumen makam anggota keluarga sultan, bangsawan, atau orang-orang penting di Kesultanan Utsmaniyah. Türbe biasanya terletak di lahan masjid. Bangunannya sendiri pada umumnya berukuran kecil dan berbentuk heksagonal atau oktagonal. Di dalam türbe biasanya terdapat satu kamar yang mungkin didekorasi dengan ubin-ubin berwarna dan ...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

United Nations resolution adopted in 2006 UN Security CouncilResolution 1729Qunaitra in the Golan HeightsDate15 December 2006Meeting no.5,596CodeS/RES/1729 (Document)SubjectThe situation in the Middle EastVoting summary15 voted forNone voted againstNone abstainedResultAdoptedSecurity Council compositionPermanent members China France Russia United Kingdom United StatesNon-permanent members Argentina Rep. of the Congo Denmark Ghana Greece&#...

Pour l’article ayant un titre homophone, voir Gaze. Pour les articles homonymes, voir Gaz (homonymie). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (novembre 2017). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à l...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

Office skyscraper in Pasig, Philippines One San Miguel AvenueGeneral informationStatusCompletedTypeOfficeLocation1 San Miguel Avenue corner Shaw Boulevard, Ortigas Center, Pasig, PhilippinesCoordinates14°34′41.02″N 121°3′27.11″E / 14.5780611°N 121.0575306°E / 14.5780611; 121.0575306Construction started1997Completed2001Opening2001OwnerAmberland CorporationHeightAntenna spire203 m (666.01 ft)Roof183 m (600.39 ft)Technical detailsFloor coun...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Trubion – news · newspapers · books · scholar · JSTOR (May 2009) (Learn how and when to remove this message) TrubionCompany typePublic companyTraded asNasdaq: TRBNIndustryBiopharmaceuticalFounded1999Fateacquired by Emergent BioSolutions (2010)HeadquartersSeattle, WAProductsProtein-based therapeuticsWe...

History of the LDS movement For a listing of denominations within the Latter Day Saint movement, see List of denominations in the Latter Day Saint movement. For a history of the largest of these denominations, see History of The Church of Jesus Christ of Latter-day Saints. This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2023) (Learn how and when to re...
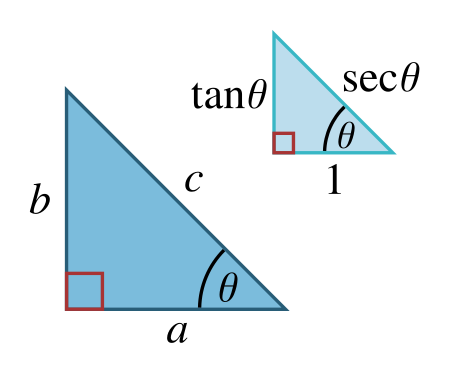
Relation between sine and cosine The Pythagorean trigonometric identity, also called simply the Pythagorean identity, is an identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one of the basic relations between the sine and cosine functions. The identity is sin 2 θ + cos 2 θ = 1. {\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1.} As usual, sin 2 θ {\displaystyle \sin ^{2...

البطولات الأسترالاسية 1923 رقم الفعالية 16 البلد أستراليا التاريخ 1923 الرياضة كرة المضرب الفعاليات البطولات الأسترالاسية 1923 – فردي رجال [لغات أخرى]، والبطولات الأسترالاسية 1923 – فردي سيدات [لغات أخرى]، والبطولات الأسترالاسية 1923 – زوجي ...

Ancient Egyptian tomb Theban tomb TT320Burial site of Pinedjem II and a Royal CachePlan of TT320TT320Coordinates25°44′12.48″N 32°36′18.13″E / 25.7368000°N 32.6050361°E / 25.7368000; 32.6050361LocationDeir el-Bahari, Theban NecropolisDiscovered1881 (Officially)← PreviousTT319Next →TT321 The Royal Cache, technically known as TT320 (previously referred to as DB320), is an Ancient Egyptian tomb located next to Deir el-Bahari, in the Theban Ne...

AwardMilitary MedalFront side of the Medalla MilitarTypeMedalAwarded forDistinguished valorPresented bySpainEligibilityMilitary personnel onlyStatusActiveEstablished1918First awardedRif War PrecedenceNext (higher)Laureate Cross of Saint Ferdinand(Royal and Military Order of Saint Ferdinand)[1]Next (lower)Cruz de Guerra The Military Medal (Spanish: Medalla Militar) is a high military award of Spain to recognise battlefield bravery. The medal was established in 1918 by Alfonso...

日本の政治家川口 順子かわぐち よりこ 2002年9月16日、アメリカ合衆国国防総省にて生年月日 (1941-01-14) 1941年1月14日(83歳)出生地 日本 東京都出身校 東京大学教養学部教養学科国際関係論分科イェール大学大学院前職 サントリー常務参議院議員現職 武蔵野大学客員教授/国際総合研究所フェロー豊田通商株式会社取締役所属政党 自由民主党(無派閥)称号 経済学修士...

Barriers used to delay pollution from decomposing trash The examples and perspective in this article deal primarily with the United States and do not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (June 2024) (Learn how and when to remove this message) A landfill in México with visible geomembrane in one of the slopes A landfill cell showing a rubberized liner in place (left) A landfill lin...