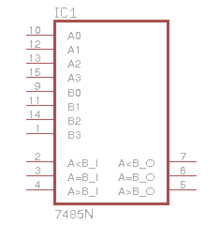
Comparador
|
Read other articles:

Sandal jepit Sandal jepit atau sandal jepang adalah sandal berwarna-warni dari karet atau karet sintetis. Tali sandal berbentuk huruf v menghubungkan bagian depan dan bagian belakang sandal. Bagian bawah sandal umumnya rata (tidak memiliki hak), sedangkan bagian atas sandal tidak memiliki penutup. Sandal jepit dipakai dengan meletakkan poros bagian depan tali sandal di antara ibu jari dan telunjuk kaki, sehingga tidak terlepas sewaktu dipakai berjalan. Selain dipakai di dalam ruang atau kamar...

Hushang Ansary Menteri KeuanganMasa jabatan1 Maret 1974 – 23 Desember 1977Perdana MenteriAmir-Abbas HoveidaJamshid Amouzegar PendahuluJamshid AmouzegarPenggantiMohammad YeganehMenteri Pariwisata dan InformasiMasa jabatan29 Desember 1971 – 1 Maret 1974Perdana MenteriAmir-Abbas Hoveida PendahuluHassan PakravanPenggantiMohammad Reza Ameli TehraniDuta Besar Iran untuk Amerika SerikatMasa jabatan25 Mei 1967 – 1 Oktober 1969Perdana MenteriAmir-Abbas Hoveida Pendahul...

Ini adalah nama Korea; marganya adalah Kim. Kim Myung-minKim Myung-min (2009)Lahir08 Oktober 1972 (umur 51)Korea SelatanPekerjaanAktorTahun aktif1996–sekarangNama KoreaHangul김명민 Hanja金明民 Alih AksaraGim Myeong-minMcCune–ReischauerKim Myŏng-min Situs webhttp://www.mmenter.com Kim Myung-min (Hangul: 김명민, lahir 8 Oktober 1972) adalah aktor asal Korea Selatan. Ia paling dikenal karena peran utamanya dalam serial televisi Immortal Admiral Yi Sun-shin (2004)...

Valentina KachoubaValentina Kachouba, dari publikasi tahun 1919.Lahir14 Mei 1898RusiaMeninggalJanuari 1997MadridNama lainValentina Kashuba, Valentine Kachouba Valentina Kachouba (14 Mei 1898 – Januari 1997), juga disebut sebagai Valentine Kashuba, adalah seorang penari balet asal Rusia. Ia menjadi anggota Ballets Russes pimpinan Diaghilev dari 1916 sampai 1921.[1] Referensi ^ Serge de Diaghileff's Ballet Russe. The Opera News. 7: 3. January 1, 1916. Pengawasan otoritas: ...

For the high school college credit course, see AP World History. Radio station in Hopewell, VirginiaWHAPHopewell, VirginiaBroadcast areaPetersburg, VirginiaFrequency1340 AM kHzBrandingThe PointProgrammingFormatCountry music[1]OwnershipOwnerBruce D. Gee and David E. Gee(Gee Communications, Inc.)HistoryFirst air dateJanuary 16, 1949[2]Call sign meaningW Hopewell And PetersburgTechnical informationFacility ID33900ClassCPower1,000 watts day and nightTransmitter coordinates37°17�...

Koordinat: 10°35′46″S 40°30′32″E / 10.596°S 40.509°E / -10.596; 40.509 Segitiga Kionga di peta tua Jerman (di bawah kanan). Segitiga Kionga (Jerman: Kionga-Dreieck) adalah wilayah kecil di pesisir timur Afrika yang terletak di antara koloni Afrika Timur Jerman (kini Tanzania) dan Mozambik Portugal (kini Mozambik). Luas wilayah ini tercatat sebesar 1000 km² (400 mi²). Segitiga Kionga merupakan wilayah Jerman dari tahun 1894 hingga 1916, dan setelah itu wil...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

At Any PricePoster rilis teatrikalSutradaraRamin BahraniProduserRamin BahraniDitulis olehRamin BahraniHallie Elizabeth NewtonPemeranZac EfronSinematograferMichael SimmondsTanggal rilis 30 Agustus 2012 (2012-08-30) (Venice) Durasi105 menitNegaraAmerika SerikatBahasaInggris At Any Price adalah film drama Amerika Serikat tahun 2012 yang disutradarai dan ditulis oleh Ramin Bahrani. Film ini dipilih untuk berkompetisi di Golden Lion pada Festival Film Venice ke-69,[1] and later sc...

Questa voce sull'argomento calciatori irlandesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Roy O'Donovan Nazionalità Irlanda Altezza 177 cm Calcio Ruolo Ala Squadra Sydney Olympic CarrieraGiovanili 2001-2004 Coventry CitySquadre di club1 2005-2007 Cork City74 (31)2007-2010 Sunderland17 (0)2008-2009→ Dundee Utd11 (1)2009→ Blackpool12 (0)2009→ Sout...

Soto tangkarTempat asalIndonesiaDaerahBetawiSunting kotak info • L • BBantuan penggunaan templat ini Soto tangkar adalah makanan khas Betawi. Nama tangkar sendiri adalah sebutan untuk iga sapi dalam bahasa Betawi pada zaman penjajahan Belanda dan sampai sekarang masih dipergunakan, meskipun sudah jarang diketahui oleh generasi saat ini.[1] Sejarah Menurut sejarahnya, pada zaman penjajahan Belanda, ketika para meneer Belanda akan mengadakan pesta, mereka biasanya memotong...

Mike ChangHarry Shum, Jr. sebagai Mike ChangPenampilanperdanaPreggersPenciptaRyan MurphyBrad FalchukIan BrennanPemeranHarry Shum, Jr.InformasiPekerjaanSiswa SMA Mike Chang adalah karakter fiksi dari serial drama Amerika produksi Fox,Glee. Karakternya diperankan oleh aktor dan penari Harry Shum, Jr., dan pertama kali tampil di Glee di episode keempatnya, Preggers. Sangat sedikit informasi yang bisa didapat mengenai Mike Chang, kecuali ia adalah anggota tim futbol sekolah fiksi William McKinley...

No Regret LifeInformasi latar belakangAsalKanoya, JepangGenreRockTahun aktif2001–sekarangLabelSpiral-MotionSitus webhttp://www.noregretlife.com/ No Regret Life adalah Band beraliran rock yang didirikan pada tahun 2001 di Kanoya, Kagoshima, Jepang, oleh Kazusō Oda, Ryuta Hashiguchi, dan Shimokariya Yuka yang kemudian digantikan oleh Genta Matsumura. Mereka merilis album pertama mereka Tomorrow is the Another Day pada November 2002. Pada bulan Mei 2003, mereka tur dengan Ellegarden. Pada bul...

Auguste ComteLahir19 Januari 1798 Montpellier (Republik Prancis Pertama) Meninggal5 September 1857 (aged 59)Paris (Kekaisaran Kedua Prancis) PekerjaanFilsuf, sosiolog, matematikawan, penulis Suami/istriCaroline Massin Auguste Comte (Nama panjang: Isidore Marie Auguste François Xavier Comte; 19 Januari 1798 – 5 September 1857)[1] adalah seorang filsuf Prancis yang dikenal karena memperkenalkan bidang ilmu sosiologi serta aliran positivis...

Questa voce sull'argomento centri abitati di Israele è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Herzliyaautorità localein ebraico הֶרְצְלִיָּה? Herzliya – VedutaVeduta LocalizzazioneStato Israele DistrettoTel Aviv SottodistrettoNon presente AmministrazioneSindacoMoshe Fadlon TerritorioCoordinate32°10′N 34°49′E32°10′N, 34°49′E (Herzliya) Altitudine39 m s.l.m. Superficie21,6 km² Abitanti93&#...

American lawyer (born 1975) Matthew GravesUnited States Attorney for the District of ColumbiaIncumbentAssumed office November 5, 2021Appointed byJoe BidenPreceded byChanning D. Phillips (acting) Personal detailsBornMatthew Michael Graves1975 (age 48–49)Reading, Pennsylvania, U.S.EducationWashington and Lee University (BA)Yale University (JD) Matthew Michael Graves (born 1975)[1] is an American lawyer who has served as the United States attorney for the District of Colum...

Head of the Catholic Church from 257 to 258 Pope SaintSixtus IIBishop of RomeFresco of Pope Sixtus II by Sandro Botticelli in the Sistine Chapel.ChurchEarly ChurchPapacy began31 August 257Papacy ended6 August 258PredecessorStephen ISuccessorDionysiusPersonal detailsBornUnknownGreece, Roman EmpireDied(258-08-06)6 August 258Rome, Roman EmpireSainthoodFeast day6/7 AugustVenerated inCatholic Church, Eastern Orthodox ChurchOther popes named Sixtus Pope Sixtus II (Greek: Πάπας Σίξτος Β�...

Cet article est une ébauche concernant l’art. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (août 2012). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donn...
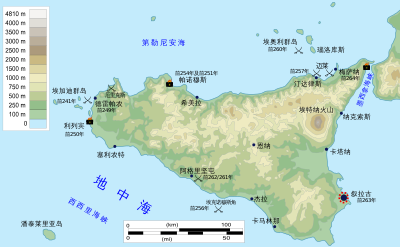
西西里行省Provincia Siciliaἐπαρχία Σικελίας羅馬帝國的行省前241年—476年约公元125年时西西里行省于罗马帝国的位置坐标:37°36′00″N 14°00′55″E / 37.599958°N 14.015378°E / 37.599958; 14.015378首府叙拉古歷史歷史時期古代史• 第一次布匿战争结束后建立 前241年• 西罗马帝国陷落 476年 前身 继承 古迦太基 叙拉古王国 西西里 (军区) 今属于 義大利&...

Constant solution to a differential equation Equilibrium point redirects here. Not to be confused with Equilibrium point (mechanics). Stability diagram classifying Poincaré maps of linear autonomous system x ′ = A x , {\displaystyle x'=Ax,} as stable or unstable according to their features. Stability generally increases to the left of the diagram.[1] Some sink, source or node are equilibrium points. In mathematics, specifically in differential equations, an equilibrium point i...

1973 song by Jeff Fortgang Some Guys Have All the LuckSingle by The Persuadersfrom the album Best Thing That Ever Happened to Me B-sideLove AttackReleasedOctober 1973Recorded1973GenreR&BLength3:29LabelAtcoSongwriter(s)Jeff FortgangProducer(s)LeBaron TaylorPhil HurttTony Bell (The Young Professionals)The Persuaders singles chronology Bad, Bold and Beautiful, Girl (1973) Some Guys Have All the Luck (1973) All Strung Out on You (1974) Some Guys Have All the Luck is a song written by Jeff For...