![]() –Δ―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–Δ―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–Δ―Ä–Η―ä–≥―ä–Μ–Ϋ–Α―²–Α –Ω―Ä–Η–Ζ–Φ–Α –Β –Ω―Ä–Η–Ζ–Φ–Α, –Ϋ–Α –Κ–Ψ―è―²–Ψ ―¹ –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β ―¹–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η―Ü–Η –Η –Η–Φ–Α ―²―Ä–Η ―¹―²―Ä–Α–Ϋ–Η―΅–Ϋ–Η ―¹―²–Β–Ϋ–Η. –½–Α―²–Ψ–≤–Α –Β –Ω–Β―²–Ψ―¹―²–Β–Ϋ (–Ω–Β–Ϋ―²–Α–Β–¥―ä―Ä) ―¹ 9 ―Ä―ä–±–Α –Η 6 –≤―ä―Ä―Ö–Α, –Ϋ–Α –Κ–Ψ–Ι―²–Ψ ―¹―²―Ä–Α–Ϋ–Η―΅–Ϋ–Η―²–Β ―¹―²–Β–Ϋ–Η –≤ –Ψ–±―â–Η―è ―¹–Μ―É―΅–Α–Ι ―¹–Α ―É―¹–Ω–Ψ―Ä–Β–¥–Ϋ–Η―Ü–Η ―¹ –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ–Ϋ–Η ―ä–≥–Μ–Η. –ê–Κ–Ψ ―²–Β ―¹–Α –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η –Κ―ä–Φ –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β, –Ω―Ä–Η–Ζ–Φ–Α―²–Α –Β –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Α. –£―ä–Ζ–Φ–Ψ–Ε–Ϋ–Ψ –Β –Β–¥–Ϋ–Α―²–Α ―¹―²―Ä–Α–Ϋ–Η―΅–Ϋ–Α ―¹―²–Β–Ϋ–Α –Ϋ–Α –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Α―²–Α –Ω―Ä–Η–Ζ–Φ–Α –¥–Α –Β –Ω―Ä–Α–≤–Ψ―ä–≥―ä–Μ–Ϋ–Η–Κ, –Α –¥―Ä―É–≥–Η―²–Β –¥–≤–Β –¥–Α ―¹–Α ―É―¹–Ω–Ψ―Ä–Β–¥–Ϋ–Η―Ü–Η βÄ™ –Κ–Ψ–≥–Α―²–Ψ –Ϋ–Α–Κ–Μ–Ψ–Ϋ―ä―² –Β –≤ –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Η–Β –Ϋ–Α –≤–Η―¹–Ψ―΅–Η–Ϋ–Α―²–Α –Κ―ä–Φ ―¹―²―Ä–Α–Ϋ–Α―²–Α –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Α―²–Α, –Κ–Ψ―è―²–Ψ –Β –Ψ–±―â–Α ―¹ –Ω―Ä–Α–≤–Ψ―ä–≥―ä–Μ–Ϋ–Η–Κ–Α.
–ü―Ä–Α–≤–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α –Β ―²–Α–Ζ–Η, –Ϋ–Α –Κ–Ψ―è―²–Ψ –≤―¹–Η―΅–Κ–Η ―¹―²―Ä–Α–Ϋ–Η―΅–Ϋ–Η ―¹―²–Β–Ϋ–Η ―¹–Α –Ω―Ä–Α–≤–Ψ―ä–≥―ä–Μ–Ϋ–Η―Ü–Η –Η ―¹–Α –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Η –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β.
–ü―Ä–Α–≤–Η–Μ–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α –Β ―²–Α–Ζ–Η, –Ϋ–Α –Κ–Ψ―è―²–Ψ –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β ―¹–Α ―Ä–Α–≤–Ϋ–Ψ―¹―²―Ä–Α–Ϋ–Ϋ–Η ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η―Ü–Η. –€–Ψ–Ε–Β –¥–Α –±―ä–¥–Β –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Α –Η–Μ–Η –Ω―Ä–Α–≤–Α.
–ï–¥–Ϋ–Ψ―Ä–Ψ–¥–Ϋ–Α―²–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α –Β –Ω―Ä–Α–≤–Η–Μ–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α ―¹ ―Ä–Α–≤–Ϋ–Η ―Ä―ä–±–Ψ–≤–Β βÄ™ ―Ä–Α–≤–Ϋ–Ψ―¹―²―Ä–Α–Ϋ–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Α –Η –Κ–≤–Α–¥―Ä–Α―²–Ϋ–Η ―¹―²―Ä–Α–Ϋ–Η.
–£―¹–Η―΅–Κ–Η ―¹–Β―΅–Β–Ϋ–Η―è, ―É―¹–Ω–Ψ―Ä–Β–¥–Ϋ–Η –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β, ―¹–Α –Β–¥–Ϋ–Α–Κ–≤–Η ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η―Ü–Η. –ü–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Η―²–Β –Κ―ä–Φ ―¹―²―Ä–Α–Ϋ–Η―΅–Ϋ–Η―²–Β ―¹―²–Β–Ϋ–Η ―¹–Α –≤ –Β–¥–Ϋ–Α –Η ―¹―ä―â–Α ―Ä–Α–≤–Ϋ–Η–Ϋ–Α, –Κ–Ψ―è―²–Ψ –Β ―É―¹–Ω–Ψ―Ä–Β–¥–Ϋ–Α –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β –Ω―Ä–Η –Ω―Ä–Α–≤–Α –Ω―Ä–Η–Ζ–Φ–Α –Η –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Α –Κ―ä–Φ ―²―è―Ö –Ω―Ä–Η –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α.
 –ù–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–ù–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–ü–Ψ–Μ―É–Ω―Ä–Α–≤–Η–Μ–Β–Ϋ (–Β–¥–Ϋ–Ψ―Ä–Ψ–¥–Ϋ–Β–Ϋ) –Φ–Ϋ–Ψ–≥–Ψ―¹―²–Β–Ϋ
–ü―Ä–Α–≤–Α―²–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α –Β –Ω–Ψ–Μ―É–Ω―Ä–Α–≤–Η–Μ–Β–Ϋ –Φ–Ϋ–Ψ–≥–Ψ―¹―²–Β–Ϋ –Η–Μ–Η –Ω–Ψ-–Ψ–±―â–Ψ ―Ä–Α–≤–Ϋ–Ψ–Φ–Β―Ä–Β–Ϋ –Φ–Ϋ–Ψ–≥–Ψ―¹―²–Β–Ϋ, –Α–Κ–Ψ –Ψ―¹–Ϋ–Ψ–≤–Α―²–Α –Β –Ω―Ä–Α–≤–Η–Μ–Β–Ϋ ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ, –Α ―¹―²―Ä–Α–Ϋ–Η―²–Β ―¹–Α –Κ–≤–Α–¥―Ä–Α―²–Η.
–Δ–Ψ–Ζ–Η –Ω–Ψ–Μ–Η–Β–¥―ä―Ä –Φ–Ψ–Ε–Β –¥–Α ―¹–Β ―Ä–Α–Ζ–≥–Μ–Β–Ε–¥–Α –Κ–Α―²–Ψ –Ω―Ä–Β―¹–Β―΅–Β–Ϋ ―²―Ä–Η―ä–≥―ä–Μ–Β–Ϋ –Ψ―¹–Ψ–Β–¥―ä―Ä, –Ω―Ä–Β–¥―¹―²–Α–≤–Β–Ϋ –Ψ―² ―¹–Η–Φ–≤–Ψ–Μ–Α –Ϋ–Α –®–Μ–Β―³–Μ–Η t{2,3}. –€–Ψ–Ε–Β –¥–Α ―¹–Β ―Ä–Α–Ζ–≥–Μ–Β–Ε–¥–Α –Η –Κ–Α―²–Ψ –¥–Η―Ä–Β–Κ―²–Ϋ–Ψ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ –Η ―¹–Β–≥–Φ–Β–Ϋ―², –Κ–Ψ–Ι―²–Ψ –Β –Ω―Ä–Β–¥―¹―²–Α–≤–Β–Ϋ –Κ–Α―²–Ψ {3}x{}.
–™―Ä―É–Ω–Α―²–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Α –Ω―Ä–Α–≤–Α –Ω―Ä–Η–Ζ–Φ–Α ―¹ ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Α –Β D3h –Ψ―² 12-―²–Η ―Ä–Β–¥. –™―Ä―É–Ω–Α―²–Α –Ϋ–Α –≤―ä―Ä―²–Β–Ϋ–Β –Β D3 –Ψ―² 6-―²–Η ―Ä–Β–¥. –™―Ä―É–Ω–Α―²–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Β ―¹―ä–¥―ä―Ä–Ε–Α ―Ü–Β–Ϋ―²―Ä–Α–Μ–Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è.
–î–≤–Ψ–Ι―¹―²–≤–Β–Ϋ–Η―è―² –Φ–Ϋ–Ψ–≥–Ψ―¹―²–Β–Ϋ –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α –Β ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –±–Η–Ω–Η―Ä–Α–Φ–Η–¥–Α. –£ ―Ö–Η–Φ–Η―è―²–Α ―²―è ―¹–Β ―¹―Ä–Β―â–Α –Ω–Ψ–¥ ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α –≤―ä–≥–Μ–Β–≤–Ψ–¥–Ψ―Ä–Ψ–¥–Α ―²―Ä–Η―ä–≥―ä–Μ–Β–Ϋ –Ω―Ä–Η–Ζ–Φ–Α–Ϋ.
–û–±–Β–Φ
 –†–Α–Ζ–Φ–Β―Ä–Η –Ζ–Α –Ψ–Ω―Ä–Β–¥–Β–Μ―è–Ϋ–Β –Ψ–±–Β–Φ–Α –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–†–Α–Ζ–Φ–Β―Ä–Η –Ζ–Α –Ψ–Ω―Ä–Β–¥–Β–Μ―è–Ϋ–Β –Ψ–±–Β–Φ–Α –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–û–±–Β–Φ―ä―² –Ϋ–Α –≤―¹―è–Κ–Α –Ω―Ä–Η–Ζ–Φ–Α –Β ―Ä–Α–≤–Β–Ϋ –Ϋ–Α –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β―²–Ψ –Ϋ–Α –Ω–Μ–Ψ―â―²–Α –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Α―²–Α –Η ―Ä–Α–Ζ―¹―²–Ψ―è–Ϋ–Η–Β―²–Ψ –Φ–Β–Ε–¥―É –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β. –£ ―¹–Μ―É―΅–Α―è, –Κ–Ψ–≥–Α―²–Ψ –Ψ―¹–Ϋ–Ψ–≤–Α―²–Α –Β ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α, –Ω―Ä–Ψ―¹―²–Ψ ―²―Ä―è–±–≤–Α –¥–Α ―¹–Β –Η–Ζ―΅–Η―¹–Μ–Η –Ω–Μ–Ψ―â―²–Α –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α –Η –¥–Α ―¹–Β ―É–Φ–Ϋ–Ψ–Ε–Η –Ω–Ψ –¥―ä–Μ–Ε–Η–Ϋ–Α―²–Α –Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α―²–Α:
 ,
,
–Κ―ä–¥–Β―²–Ψ  –Β –¥―ä–Μ–Ε–Η–Ϋ–Α―²–Α –Ϋ–Α ―¹―²―Ä–Α–Ϋ–Α―²–Α –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Α―²–Α,
–Β –¥―ä–Μ–Ε–Η–Ϋ–Α―²–Α –Ϋ–Α ―¹―²―Ä–Α–Ϋ–Α―²–Α –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Α―²–Α,  –Β –≤–Η―¹–Ψ―΅–Η–Ϋ–Α―²–Α –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α –Η
–Β –≤–Η―¹–Ψ―΅–Η–Ϋ–Α―²–Α –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α –Η  –Β ―Ä–Α–Ζ―¹―²–Ψ―è–Ϋ–Η–Β―²–Ψ –Φ–Β–Ε–¥―É –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β (–≤–Η―¹–Ψ―΅–Η–Ϋ–Α―²–Α –Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α―²–Α).
–Β ―Ä–Α–Ζ―¹―²–Ψ―è–Ϋ–Η–Β―²–Ψ –Φ–Β–Ε–¥―É –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β (–≤–Η―¹–Ψ―΅–Η–Ϋ–Α―²–Α –Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α―²–Α).
–ü–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α
–û–Κ–Ψ–Μ–Ϋ–Α―²–Α –Η –Ω―ä–Μ–Ϋ–Α―²–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α ―¹–Β –Ϋ–Α–Φ–Η―Ä–Α―² –Ω–Ψ –Ψ–±―â–Η―²–Β ―³–Ψ―Ä–Φ―É–Μ–Η –Ζ–Α –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α, –Κ–Ψ–≥–Α―²–Ψ –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β ―¹–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η―Ü–Η. –Δ–Β –Φ–Ψ–≥–Α―² –¥–Α ―¹–Β –Ω–Ψ–Μ―É―΅–Α―² –Ψ―² ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α ―Ä–Α–Ζ–≥―ä–Ϋ–Α―²–Α –Ω―Ä–Η–Ζ–Φ–Α, –Κ–Ψ―è―²–Ψ ―¹―ä–¥―ä―Ä–Ε–Α 3 ―É―¹–Ω–Ψ―Ä–Β–¥–Ϋ–Η–Κ–Α –Η 2 –Β–¥–Ϋ–Α–Κ–≤–Η ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α.
–ù–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–ù–Β–Κ–Α  –Η
–Η  ―¹–Α ―¹―²―Ä–Α–Ϋ–Η―²–Β –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β,
―¹–Α ―¹―²―Ä–Α–Ϋ–Η―²–Β –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β,  –Β –Ψ–Κ–Ψ–Μ–Ϋ–Η―è―² ―Ä―ä–±, –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ –Ω–Ψ–¥ ―ä–≥―ä–Μ
–Β –Ψ–Κ–Ψ–Μ–Ϋ–Η―è―² ―Ä―ä–±, –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ –Ω–Ψ–¥ ―ä–≥―ä–Μ  –Κ―ä–Φ –Ψ―¹–Ϋ–Ψ–≤–Α―²–Α, –Α
–Κ―ä–Φ –Ψ―¹–Ϋ–Ψ–≤–Α―²–Α, –Α  –Β –≤–Η―¹–Ψ―΅–Η–Ϋ–Α―²–Α –Ϋ–Α –Ψ–Κ–Ψ–Μ–Ϋ–Η―²–Β ―¹―²–Β–Ϋ–Η. –û–Κ–Ψ–Μ–Ϋ–Α―²–Α (―¹―²―Ä–Α–Ϋ–Η―΅–Ϋ–Α) –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α
–Β –≤–Η―¹–Ψ―΅–Η–Ϋ–Α―²–Α –Ϋ–Α –Ψ–Κ–Ψ–Μ–Ϋ–Η―²–Β ―¹―²–Β–Ϋ–Η. –û–Κ–Ψ–Μ–Ϋ–Α―²–Α (―¹―²―Ä–Α–Ϋ–Η―΅–Ϋ–Α) –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α  –Β ―¹―É–Φ–Α –Ψ―² –Ω–Μ–Ψ―â–Η―²–Β –Ϋ–Α 3 ―É―¹–Ω–Ψ―Ä–Β–¥–Ϋ–Η–Κ–Α ―¹―ä―¹ ―¹―²―Ä–Α–Ϋ–Η
–Β ―¹―É–Φ–Α –Ψ―² –Ω–Μ–Ψ―â–Η―²–Β –Ϋ–Α 3 ―É―¹–Ω–Ψ―Ä–Β–¥–Ϋ–Η–Κ–Α ―¹―ä―¹ ―¹―²―Ä–Α–Ϋ–Η  –Η
–Η  , –Κ–Ψ–Η―²–Ψ ―¹–Κ–Μ―é―΅–≤–Α―² ―ä–≥―ä–Μ
, –Κ–Ψ–Η―²–Ψ ―¹–Κ–Μ―é―΅–≤–Α―² ―ä–≥―ä–Μ  ―¹ –Ψ–±―â–Α―²–Α –Η–Φ ―¹―²―Ä–Α–Ϋ–Α
―¹ –Ψ–±―â–Α―²–Α –Η–Φ ―¹―²―Ä–Α–Ϋ–Α  .
.
–ü–Μ–Ψ―â―²–Α –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Η―²–Β  –Β ―¹―É–Φ–Α –Ψ―² –Μ–Η―Ü–Α―²–Α –Ϋ–Α –¥–≤–Α –Β–¥–Ϋ–Α–Κ–≤–Η ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α –Η –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ψ–Ω―Ä–Β–¥–Β–Μ–Η –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α –Ϋ–Α –Ξ–Β―Ä–Ψ–Ϋ, –Α –Ω―ä–Μ–Ϋ–Α―²–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α
–Β ―¹―É–Φ–Α –Ψ―² –Μ–Η―Ü–Α―²–Α –Ϋ–Α –¥–≤–Α –Β–¥–Ϋ–Α–Κ–≤–Η ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α –Η –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ψ–Ω―Ä–Β–¥–Β–Μ–Η –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α –Ϋ–Α –Ξ–Β―Ä–Ψ–Ϋ, –Α –Ω―ä–Μ–Ϋ–Α―²–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α  –Β ―¹―É–Φ–Α –Ψ―² –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Α―²–Α –Η –Ψ–Κ–Ψ–Μ–Ϋ–Α―²–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Η.
–Β ―¹―É–Φ–Α –Ψ―² –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Α―²–Α –Η –Ψ–Κ–Ψ–Μ–Ϋ–Α―²–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Η.
 –†–Α–Ζ–≥―ä–Ϋ–Α―²–Α –Β–¥–Ϋ–Ψ―Ä–Ψ–¥–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–†–Α–Ζ–≥―ä–Ϋ–Α―²–Α –Β–¥–Ϋ–Ψ―Ä–Ψ–¥–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
- –û–Κ–Ψ–Μ–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α
 –Η–Μ–Η
–Η–Μ–Η
- –û―¹–Ϋ–Ψ–≤–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α
 ,
,
–Κ―ä–¥–Β―²–Ψ  –Β –Ω–Ψ–Μ―É–Ω–Β―Ä–Η–Φ–Β―²―ä―Ä―ä―² –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α.
–Β –Ω–Ψ–Μ―É–Ω–Β―Ä–Η–Φ–Β―²―ä―Ä―ä―² –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α.
- –ü―ä–Μ–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α
 –Η–Μ–Η
–Η–Μ–Η .
.
–ü―Ä–Α–≤–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–ü―Ä–Η –Ω―Ä–Α–≤–Α―²–Α –Ω―Ä–Η–Ζ–Φ–Α –Ψ–Κ–Ψ–Μ–Ϋ–Η―è―² ―Ä―ä–± –Β –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Β–Ϋ –Ϋ–Α –Ψ―¹–Ϋ–Ψ–≤–Α―²–Α (Έ±=90¬Α) –Η ―¹―ä–≤–Ω–Α–¥–Α ―¹ –≤–Η―¹–Ψ―΅–Η–Ϋ–Α―²–Α –Ϋ–Α ―¹―²―Ä–Α–Ϋ–Η―΅–Ϋ–Α―²–Α ―¹―²–Β–Ϋ–Α  .
.
- –û–Κ–Ψ–Μ–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α

- –û―¹–Ϋ–Ψ–≤–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α

- –ü―ä–Μ–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α
 .
.
–ü―Ä–Α–≤–Η–Μ–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–û―¹–Ϋ–Ψ–≤–Ϋ–Η―²–Β ―Ä―ä–±–Ψ–≤–Β ―¹–Α ―Ä–Α–≤–Ϋ–Η  .
.
 –ö–Ψ–Ϋ―³–Η–≥―É―Ä–Α―Ü–Η―è –Ϋ–Α –≤―ä―Ä―Ö–Α –Ζ–Α –Β–¥–Ϋ–Ψ―Ä–Ψ–¥–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–ö–Ψ–Ϋ―³–Η–≥―É―Ä–Α―Ü–Η―è –Ϋ–Α –≤―ä―Ä―Ö–Α –Ζ–Α –Β–¥–Ϋ–Ψ―Ä–Ψ–¥–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–ï–¥–Ϋ–Ψ―Ä–Ψ–¥–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–£―¹–Η―΅–Κ–Η ―Ä―ä–±–Ψ–≤–Β ―¹–Α ―Ä–Α–≤–Ϋ–Η  .
.
- –û–Κ–Ψ–Μ–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α

- –û―¹–Ϋ–Ψ–≤–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α

- –ü―ä–Μ–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Η–Ϋ–Α
 .
.
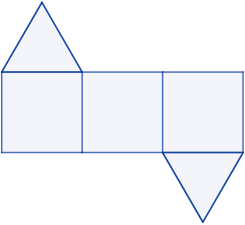
 –ü―Ä–Β―¹–Β―΅–Β–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–ü―Ä–Β―¹–Β―΅–Β–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–ü―Ä–Β―¹–Β―΅–Β–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α
–ü―Ä–Β―¹–Β―΅–Β–Ϋ–Α―²–Α –Ω―Ä–Α–≤–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α –Η–Φ–Α –Ω―Ä–Β―¹–Β―΅–Β–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω–Ψ–≤―ä―Ä―Ö–Ϋ–Ψ―¹―² –Ω–Ψ–¥ –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ ―ä–≥―ä–Μ. [1]
–û–±–Β–Φ―ä―² –Ϋ–Α –Ω―Ä–Β―¹–Β―΅–Β–Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α ―¹ –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Α –Ω–Μ–Ψ―â  –Η ―²―Ä–Η –≤–Η―¹–Ψ―΅–Η–Ϋ–Η
–Η ―²―Ä–Η –≤–Η―¹–Ψ―΅–Η–Ϋ–Η  –Η
–Η  ―¹–Β –Ψ–Ω―Ä–Β–¥–Β–Μ―è –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α [2]
―¹–Β –Ψ–Ω―Ä–Β–¥–Β–Μ―è –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α [2]

–‰–Φ–Α –Ω―ä–Μ–Ϋ–Α D2h ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Α ―¹–Β―΅–Β–Ϋ–Η―è―²–Α –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Α –Ω―Ä–Η–Ζ–Φ–Α –±–Β–Ζ ―¹―ä–Ζ–¥–Α–≤–Α–Ϋ–Β –Ϋ–Α –Ϋ–Ψ–≤–Η –≤―ä―Ä―Ö–Ψ–≤–Β (–Ω―Ä–Β―¹–Η―΅–Α–Ϋ–Β―²–Ψ –Ϋ–Α ―Ä―ä–±–Ψ–≤–Β –Ϋ–Β ―¹–Β ―¹―΅–Η―²–Α –Ζ–Α –Ϋ–Ψ–≤ –≤―Ä―ä―Ö). –ü–Ψ–Μ―É―΅–Β–Ϋ–Η―²–Β –Φ–Ϋ–Ψ–≥–Ψ―¹―²–Β–Ϋ–Η –Η–Φ–Α―² ―¹ 6 ―¹―²–Β–Ϋ–Η ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Η ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η―Ü–Η: –Β–¥–Η–Ϋ –Φ–Ϋ–Ψ–≥–Ψ―¹―²–Β–Ϋ, –Ζ–Α–Ω–Α–Ζ–≤–Α―â –Ψ―Ä–Η–≥–Η–Ϋ–Α–Μ–Ϋ–Η―²–Β –≥–Ψ―Ä–Ϋ–Η –Η –¥–Ψ–Μ–Ϋ–Η ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η―Ü–Η, –Η –Β–¥–Η–Ϋ, –Ζ–Α–Ω–Α–Ζ–≤–Α―â –Ψ―Ä–Η–≥–Η–Ϋ–Α–Μ–Ϋ–Η―²–Β –Κ–≤–Α–¥―Ä–Α―²–Η. –î–≤–Β―²–Β ―¹–Η–Φ–Β―²―Ä–Η–Η –Ϋ–Α ―¹–Β―΅–Β–Ϋ–Η–Β―²–Ψ C3v –Η–Φ–Α―² –Β–¥–Η–Ϋ –Ψ―¹–Ϋ–Ψ–≤–Β–Ϋ ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ, 3 ―¹―²―Ä–Α–Ϋ–Η―΅–Ϋ–Η ―¹–Α–Φ–Ψ–Ω―Ä–Β―¹–Η―΅–Α―â–Η ―¹–Β –Κ–≤–Α–¥―Ä–Α―²–Α –Η 3 ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Η ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α.
–Γ–≤―ä―Ä–Ζ–Α–Ϋ–Η –Φ–Ϋ–Ψ–≥–Ψ―¹―²–Β–Ϋ–Η –Η –Ω–Α–Ϋ–Α
–Γ–≤―ä―Ä–Ζ–Α–Ϋ–Η –Κ―É–Ω–Ψ–Μ–Η
–Γ–≤―ä―Ä–Ζ–Α–Ϋ–Η –Ω―Ä–Η–Ζ–Φ–Η
|
–Γ―ä–Β–¥–Η–Ϋ–Β–Ϋ–Η―è
–ü–Η―²–Η
|
–£–Η–Ε―²–Β ―¹―ä―â–Ψ
–‰–Ζ―²–Ψ―΅–Ϋ–Η―Ü–Η