–ö–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į –≤ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—ā–į –≥–Ľ–į—Ā–ł:
–ö–≤–į–ī—Ä–į—ā—ä—ā –Ĺ–į –ļ–ĺ—Ź –ī–į –Ķ —Ā—ā—Ä–į–Ĺ–į –≤ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –Ķ —Ä–į–≤–Ķ–Ĺ –Ĺ–į —Ā–Ī–ĺ—Ä–į –ĺ—ā –ļ–≤–į–ī—Ä–į—ā–ł—ā–Ķ –Ĺ–į –ī—Ä—É–≥–ł—ā–Ķ –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł –ľ–ł–Ĺ—É—Ā —É–ī–≤–ĺ–Ķ–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –Ĺ–į —ā–Ķ–∑–ł –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā–į –Ĺ–į —ä–≥—ä–Ľ–į, –∑–į–ļ–Ľ—é—á–Ķ–Ĺ –ľ–Ķ–∂–ī—É —ā—Ź—Ö.
–†–į–∑–≥–Ľ–Ķ–∂–ī–į —Ā–Ķ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ  —Ā—ä—Ā —Ā—ā—Ä–į–Ĺ–ł
—Ā—ä—Ā —Ā—ā—Ä–į–Ĺ–ł  ,
,  –ł
–ł  (—Ą–ł–≥. 1).
(—Ą–ł–≥. 1).
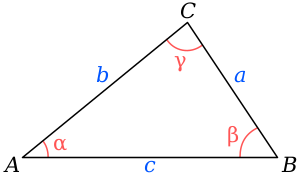 –§–ł–≥. 1. –ö–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į.
–§–ł–≥. 1. –ö–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į.
–Ę–ĺ–≥–į–≤–į –Ķ –≤ —Ā–ł–Ľ–į —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ—ā–ĺ

–Ę—É–ļ, —Ā  —Ā–Ķ –ĺ–∑–Ĺ–į—á–į–≤–į —ä–≥—ä–Ľ—ä—ā, –∑–į–ļ–Ľ—é—á–Ķ–Ĺ –ľ–Ķ–∂–ī—É
—Ā–Ķ –ĺ–∑–Ĺ–į—á–į–≤–į —ä–≥—ä–Ľ—ä—ā, –∑–į–ļ–Ľ—é—á–Ķ–Ĺ –ľ–Ķ–∂–ī—É  –ł
–ł  . –ó–į —Ā—ā—Ä–į–Ĺ–ł—ā–Ķ
. –ó–į —Ā—ā—Ä–į–Ĺ–ł—ā–Ķ  –ł
–ł  –ļ–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ł–∑–≥–Ľ–Ķ–∂–ī–į —ā–į–ļ–į:
–ļ–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ł–∑–≥–Ľ–Ķ–∂–ī–į —ā–į–ļ–į:


–ě—ā—ā—É–ļ –Ľ–Ķ—Ā–Ĺ–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –ł–∑—Ä–į–∑—Ź—ā –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā–ł—ā–Ķ –Ĺ–į –ī–į–ī–Ķ–Ĺ–ł—ā–Ķ —ä–≥–Ľ–ł:


 .
.
–ö–ĺ–≥–į—ā–ĺ –Ķ–ī–ł–Ĺ –ĺ—ā —ä–≥–Ľ–ł—ā–Ķ –Ĺ–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –Ķ –Ņ—Ä–į–≤, –ļ–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į —Ā–Ķ —Ā–≤–Ķ–∂–ī–į –ī–ĺ –ü–ł—ā–į–≥–ĺ—Ä–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į.
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–į
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ —Ā –ü–ł–≥–į–≥–ĺ—Ä–ĺ–≤–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į
–Ě–Ķ–ļ–į –ī–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į  . –ě—ā –≤—ä—Ä—Ö–į
. –ě—ā –≤—ä—Ä—Ö–į  –ļ—ä–ľ —Ā—ā—Ä–į–Ĺ–į—ā–į
–ļ—ä–ľ —Ā—ā—Ä–į–Ĺ–į—ā–į  –Ķ —Ā–Ņ—É—Ā–Ĺ–į—ā–į –≤–ł—Ā–ĺ—á–ł–Ĺ–į—ā–į
–Ķ —Ā–Ņ—É—Ā–Ĺ–į—ā–į –≤–ł—Ā–ĺ—á–ł–Ĺ–į—ā–į  (—Ą–ł–≥. 2). –ě—ā —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į
(—Ą–ł–≥. 2). –ě—ā —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į  —Ā–Ľ–Ķ–ī–≤–į:
—Ā–Ľ–Ķ–ī–≤–į:
 –§–ł–≥. 2. –Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –Ĺ–į –ļ–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į.
–§–ł–≥. 2. –Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –Ĺ–į –ļ–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į.
 ,
,
–ü–ł—ā–į–≥–ĺ—Ä–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į –∑–į –ī–≤–į—ā–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į  –ł
–ł  —Ā–Ķ –∑–į–Ņ–ł—Ā–≤–į –≤—ä–≤ –≤–ł–ī–į
—Ā–Ķ –∑–į–Ņ–ł—Ā–≤–į –≤—ä–≤ –≤–ł–ī–į
 .
.
–ě—á–Ķ–≤–ł–ī–Ĺ–ĺ, –ī–Ķ—Ā–Ĺ–ł—ā–Ķ —á–į—Ā—ā–ł –Ĺ–į –ī–≤–Ķ—ā–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź —Ā–į —Ä–į–≤–Ĺ–ł, —ā.–Ķ.
 .
.
–°–Ľ–Ķ–ī –ĺ–Ņ—Ä–ĺ—Ā—ā—Ź–≤–į–Ĺ–Ķ —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į
 .
.
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ —Ā –≤–Ķ–ļ—ā–ĺ—Ä–ł
–í—ä–≤–Ķ–∂–ī–į—ā —Ā–Ķ –Ī–į–∑–ł—Ā–Ĺ–ł—ā–Ķ –≤–Ķ–ļ—ā–ĺ—Ä–ł  –ł
–ł  .
.
–Ě–Ķ–ļ–į  . –ü–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ –∑–į –ł–∑–≤–į–∂–ī–į–Ĺ–Ķ –Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–ł —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į:
. –ü–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ –∑–į –ł–∑–≤–į–∂–ī–į–Ĺ–Ķ –Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–ł —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į:

–°–Ľ–Ķ–ī –Ņ–ĺ–≤–ī–ł–≥–į–Ĺ–Ķ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā —Ā–Ķ –ī–ĺ—Ā—ā–ł–≥–į –ī–ĺ —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ—ā–ĺ

–ě—ā —Ą–ĺ—Ä–ľ—É–Ľ–į—ā–į –∑–į —Ā–ļ–į–Ľ–į—Ä–Ĺ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –Ĺ–į –ī–≤–į –≤–Ķ–ļ—ā–ĺ—Ä–į —Ā—ā–į–≤–į —Ź—Ā–Ĺ–ĺ, —á–Ķ

–° —ā–ĺ–≤–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į—ā–į –Ķ –ī–ĺ–ļ–į–∑–į–Ĺ–į.
–í–ł–∂—ā–Ķ —Ā—ä—Č–ĺ