Read other articles:

Oktovianus Mainmani Informasi pribadiNama lengkap Oktovianus MainmaniTanggal lahir 27 Oktober 1990 (umur 33)Tempat lahir Jayapura, Papua, IndonesiaTinggi 1,67 m (5 ft 5+1⁄2 in)Posisi bermain WingerInformasi klubKlub saat ini PSBS BIAKNomor 28Karier senior*Tahun Tim Tampil (Gol)2008–2009 PSMS Medan 24 (1)2009 (6 bulan) Persidafon Dafonsoro 7 (0)2010 (6 bulan) Persitara Jakarta Utara 13 (2)2010–2011 Sriwijaya 15 (3)2011–2012 Persiram Raja Ampat 19 (3)2013 Persit...

United States Senate election in New Jersey 1922 United States Senate election in New Jersey ← 1916 November 7, 1922 1928 →   Nominee Edward I. Edwards Joseph S. Frelinghuysen Sr. Party Democratic Republican Popular vote 451,832 362,699 Percentage 54.87% 44.05% County results Edwards:      50–60%      70–80% Frelinghuysen:      40–50%      50–60%  &#...

Deakin government (II)In office5 July 1905 – 13 November 1908MonarchEdward VIIPrime MinisterAlfred DeakinPartyProtectionistStatusMinority (Labor support)OriginPredecessor lost confidence motionDemiseLost confidence motionPredecessorReid governmentSuccessorFisher government (I) The second Deakin government was the period of federal executive government of Australia led by Prime Minister Alfred Deakin. It lasted from 5 July 1905 to 13 November 1908. Deakin was the second prime minister ...

Diversion of civilian flights from US airspace into Canada after 9/11 Operation Yellow RibbonLocationCanadaOrganised byTransport Canada Gander International Airport in Newfoundland, Canada, played host to 38 airliners, totaling 6,122 passengers and 473 crew, as part of Operation Yellow Ribbon. Operation Yellow Ribbon (French: Opération ruban jaune) was commenced by Canada to handle the diversion of civilian airline flights in response to the September 11 attacks in 2001 in the United States....

Эту страницу предлагается объединить со страницей Либеральное масонство.Пояснение причин и обсуждение — на странице Википедия:К объединению/6 декабря 2022.Обсуждение длится не менее недели (подробнее). Не удаляйте шаблон до подведения итога обсуждения. Свобода, Равенств�...

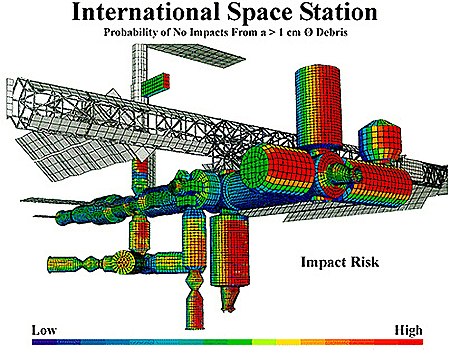
Elemen manajemen risiko Contoh penilaian risiko: Sebuah model NASA yang menunjukkan area berisiko tinggi terkena dampak untuk Stasiun Luar Angkasa Internasional Manajemen risiko adalah suatu pendekatan terstruktur atau metodologi dalam mengelola ketidakpastian yang berkaitan dengan ancaman; suatu rangkaian aktivitas manusia termasuk: Penilaian risiko, pengembangan strategi untuk mengelolanya dan mitigasi risiko dengan menggunakan pemberdayaan atau pengelolaan sumberdaya. Strategi yang dapat d...

Species of fish This article is about the species of fish. For other uses, see Wahoo (disambiguation). Wahoo Wahoo Conservation status Least Concern  (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Scombriformes Family: Scombridae Tribe: Scomberomorini Genus: AcanthocybiumGill, 1862 Species: A. solandri Binomial name Acanthocybium solandri(Cuvier in Cuvier and Valenciennes, 1832)[2] Synonyms ...

Art and craft of writing screenplays Example of a page from a screenplay formatted for a feature-length film. Screenwriting or scriptwriting is the art and craft of writing scripts for mass media such as feature films, television productions or video games. It is often a freelance profession. Screenwriters are responsible for researching the story, developing the narrative, writing the script, screenplay, dialogues and delivering it, in the required format, to development executives. Screenwr...

The Buddha of Suburbia Саундтрек Дэвида Боуи Дата выпуска 8 ноября 199324 октября 1995 (США) Место записи Mountain Studios, Монтрё, Швейцария Жанры Рок, эмбиент Длительность 55:26 Продюсеры Дэвид Боуи и Дэвид Ричардс Лейбл BMG International Профессиональные рецензии All Music Guide ссылка Роберт Кристгау ссы�...

بول نيومان (بالإنجليزية: Paul Newman)‏    معلومات شخصية اسم الولادة بول لنرد نيومان الميلاد 26 يناير 1925(1925-01-26)شاكير هايتس، أوهايو الوفاة 26 سبتمبر 2008 (83 سنة)ويستبورت  سبب الوفاة سرطان الرئة مواطنة الولايات المتحدة  لون الشعر شعر بني  الطول 177 سنتيمتر[1]  الزوجة جو...

Tanpa kekerasanPahatan di markas besar Perserikatan Bangsa-Bangsa di New York CitySenimanCarl Fredrik ReuterswärdTahun1985 (1985)TipePahatanLokasiNew York Tanpa kekerasan[1] adalah sebuah pahatan perunggu karya artis Swedia Carl Fredrik Reuterswärd. Carl membuat pahatan tersebut setelah penyanyi, penulis lagu dan aktivis perdamaian John Lennon dibunuh.[2] Saat ini, terdapat 17 salinan pahatan tersebut di seluruh dunia, sepuluh diantaranya ada di Swedia. Referensi Wikime...

В Википедии есть статьи о других людях с такой фамилией, см. Беннетт; Беннетт, Джеймс Гордон. Джеймс Гордон Беннетт (младший)англ. James Gordon Bennett, Jr. Дата рождения 10 мая 1841(1841-05-10) Место рождения Нью-Йорк, США Дата смерти 14 мая 1918(1918-05-14) (77 лет) Место смерти Больё-сюр-Мер, Фр�...

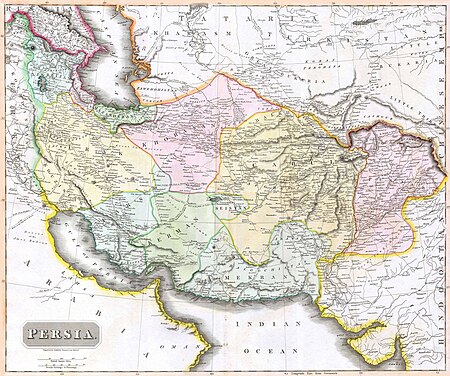
اللعبة الكبرىمعلومات عامةتاريخ البدء 12 يناير 1830 تاريخ الانتهاء 10 سبتمبر 1895 المشاركون المملكة المتحدة لبريطانيا العظمى وأيرلنداالإمبراطورية الروسية تعديل - تعديل مصدري - تعديل ويكي بيانات بلاد فارس في بداية اللعبة الكبرى سنة 1814 آسيا الوسطى حوالي سنة 1848 جزء من سلسلة حول تا�...

Independent city in Virginia Independent city in Virginia, United StatesStauntonIndependent cityFrederick Street FlagSealNickname: Queen City of the Shenandoah ValleyLocation of Staunton in the Commonwealth of VirginiaStauntonShow map of Shenandoah ValleyStauntonShow map of VirginiaStauntonShow map of the United StatesCoordinates: 38°9′29″N 79°4′35″W / 38.15806°N 79.07639°W / 38.15806; -79.07639CountryUnited StatesStateVirginiaCountyNone (Independent ...

External body part of a spider This article is about the spider or insect organ. For other uses, see Spinneret (disambiguation). The spinnerets of an Australian garden orb weaver spider. Black spinneret of Phidippus adumbratus visible below red abdomen A spinneret is a silk-spinning organ of a spider or the larva of an insect. Some adult insects also have spinnerets, such as those borne on the forelegs of Embioptera.[1] Spinnerets are usually on the underside of a spider's opisthosoma...

You can help expand this article with text translated from the corresponding article in Russian. (August 2020) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears unreliable or low...

U.S. state This article is about the U.S. state. For other uses, see South Carolina (disambiguation). State in the United StatesSouth CarolinaState FlagSealNickname: The Palmetto StateMotto(s): Dum spiro speroWhile I breathe, I hopeAnimis opibusque paratiPrepared in mind and resourcesAnthem: CarolinaSouth Carolina on my MindMap of the United States with South Carolina highlightedCountryUnited StatesBefore statehoodProvince of South CarolinaAdmitted to the UnionMay 23, 1788 (8th stat...

Miroslava Koželuhová BendlováNazionalità Cecoslovacchia Tennis Carriera Singolare1 Vittorie/sconfitte 4-5 Titoli vinti 1 Miglior ranking Risultati nei tornei del Grande Slam  Australian Open  Roland Garros QF (1978)  Wimbledon  US Open Doppio1 Vittorie/sconfitte 1-3 Titoli vinti 0 Miglior ranking Risultati nei tornei del Grande Slam  Australian Open  Roland Garros 2T (1975)  Wimbledon  US Open 1 Dati relativi al circuito maggiore professionisti...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: June–August 2012 Hakkari clashes – news · newspapers · books · scholar · JSTOR (July 2012) (Learn how and when to remove this message) This article reads like ...

Finite sets whose elements are all hereditarily finite sets In mathematics and set theory, hereditarily finite sets are defined as finite sets whose elements are all hereditarily finite sets. In other words, the set itself is finite, and all of its elements are finite sets, recursively all the way down to the empty set. Formal definition A recursive definition of well-founded hereditarily finite sets is as follows: Base case: The empty set is a hereditarily finite set. Recursion rule: If a 1 ...