Teoría de los orbitales moleculares
|
Read other articles:

The RubyAlbum mini karya AprilDirilis16 Oktober 2018 (2018-10-16)Direkam2018Genreretrodance-popsynth-popDurasi16:26BahasaKoreanLabelDSP MediaKakao MKronologi April The Blue(2018) The Ruby(2018) Da Capo(2020) Singel dalam album The Ruby Oh! My MistakeDirilis: 16 Oktober 2018 The Ruby adalah album mini keenam oleh grup musik wanita Korea Selatan April. Album ini dirilis pada 16 Oktober 2018, oleh DSP Media. Album mini ini dibarengi oleh singel utama retro Oh! My Mistake.[1] The...

Montaldo Bormida commune di Italia Tempat Negara berdaulatItaliaRegion di ItaliaPiedmontProvinsi di ItaliaProvinsi Alessandria NegaraItalia Ibu kotaMontaldo Bormida PendudukTotal605 (2023 )GeografiLuas wilayah5,72 km² [convert: unit tak dikenal]Ketinggian334 m Berbatasan denganOrsara Bormida Sezzadio Trisobbio Carpeneto Rivalta Bormida SejarahSanto pelindungMikhael Informasi tambahanKode pos15010 Zona waktuUTC+1 UTC+2 Kode telepon0143 ID ISTAT006104 Kode kadaster ItaliaF404 Lain-l...

English sculptor Gilbert LedwardPhoto portrait of Gilbert Ledward by Bassano Ltd (1937)Born(1888-01-23)23 January 1888Died21 June 1960(1960-06-21) (aged 72)Known forSculptureParentRichard Arthur Ledward (father)RelativesPercy Hague Jowett (brother-in-law)AwardsMedal of Merit (Czech Republic)Otto Beit Medal Gilbert Ledward OBE RA[1] (23 January 1888 – 21 June 1960), was an English sculptor. He won the British Prix de Rome for sculpture in 1913, and in World War I served...

Dewi Tara, Tibet, 1993 Tara atau Ārya Tārā (dikenal juga sebagai Jetsun Dolma dalam bahasa Tibet) adalah figur suci wanita Buddha (Boddhisattva) yang masih diamalkan dan dilestarikan sampai sekarang sebagai tantra Buddha dalam agama Buddha Tibet. Tara atau dewi Tara merupakan lambang dari kebebasan/ kemerdekaan jiwa, dan menyatakan keberhasilan dan prestasi hidup yang sejati dan bersifat suci. Dewi Tara juga merupakan lambang dari belas kasih serta kehampaan (Śūnyatā, ketidak beradaan d...

Chinese American man with queue in San Francisco's Chinatown The Pigtail Ordinance was an 1873 law intended to force prisoners in San Francisco, California to have their hair cut within an inch of the scalp. It affected Qing Chinese prisoners in particular, as it meant they would have their queue, a waist-long, braided pigtail, cut off. The proposal passed by a narrow margin through the San Francisco Board of Supervisors in 1873 but was vetoed by the mayor. An identical version of the law was...

American politician Joseph D. EarlyMember of the U.S. House of Representativesfrom Massachusetts's 3rd districtIn officeJanuary 3, 1975 – January 3, 1993Preceded byHarold DonohueSucceeded byPeter I. BluteMember of the Massachusetts House of RepresentativesIn office1963–1974 Personal detailsBornJoseph Daniel EarlyJanuary 31, 1933Worcester, MassachusettsDiedNovember 9, 2012(2012-11-09) (aged 79)Worcester, MassachusettsResting placeSaint John's Cemetery, Worcester, ...

British politician (born 1962) The Right HonourableChris GraylingMPOfficial portrait, 2020Secretary of State for TransportIn office14 July 2016 – 24 July 2019Prime MinisterTheresa MayPreceded byPatrick McLoughlinSucceeded byGrant ShappsLeader of the House of CommonsIn office9 May 2015 – 13 July 2016Prime MinisterDavid CameronPreceded byWilliam HagueSucceeded byDavid LidingtonLord President of the CouncilIn office9 May 2015 – 14 July 2016Prime MinisterDavid Cam...

Pemilihan umum Gubernur Bali 20031998200830 Juli 20036 Agustus 2003Kandidat Calon Gede Ngurah Wididana Dewa Made Beratha Tjokorda Gde Budi Suryawan Partai Fraksi Kesatuan Indonesia dan Fraksi Partai Golongan Karya Fraksi Partai Demokrasi Indonesia Perjuangan Fraksi Kesatuan Indonesia Pendamping I Putu Gede Ary Suta I Gusti Ngurah Kesuma Kelakan Anak Agung Hardiana Calon Anak Agung Gede Antara Partai Fraksi Partai Golongan Karya Pendamping Jro Gde Karang Tangkid Suwarsana Peta p...

Hong Kong retailer This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: A.S. Watson Group – news · newspapers · books · scholar · JSTOR (December 2016) (Learn how and when to remove this message) AS Watson Group (Hong Kong) Ltd.Head office at Watson House in Fo TanIndustryHealth & Beauty RetailFounded1828;...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يوليو 2019) الحدثكأس الكؤوس الأوروبية 1992–93 نادي بارما رويال أنتويرب 3 1 التاريخ12 مايو 1993 الملعبملعب ويمبلي الح�...

Former slave and later public figure (c. 1736 – 1770) William Ansah SessarakooBornc. 1736AnomaboDiedc. 1770Occupation(s)Public figure, diplomat, slave traderKnown forTraveling to England as the Royal African William Ansah Sessarakoo (c. 1736 – 1770), a prominent 18th-century Fante royal and diplomat, best known for his enslavement in the West Indies and diplomatic mission to England. He was both prominent among the Fante people and influential among Europeans concerned with the trans...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: モールス符号 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2015年2月) 「SOS」のモールス符号 モールス符号(モー�...
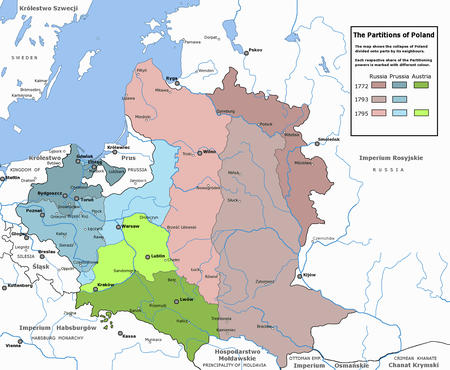
Former territories of the Polish–Lithuanian Commonwealth invaded by the Russian Empire For other territories annexed, see Prussian Partition and Austrian Partition. The Russian PartitionThe CommonwealthThe Polish–Lithuanian Commonwealth in 1772EliminationThe three partitions of the Polish–Lithuanian Commonwealth. The Russian Partition (red), the Austrian Partition (green), and the Prussian Partition (blue) The Russian Partition (Polish: zabór rosyjski), sometimes called Russian Poland,...

Modern genre of music sung in many churches Worship music redirects here. For Anthrax's album, see Worship Music (album). For music named Worship, see Worship (disambiguation). Praise music redirects here. For music named Praise or by Praise, see Praise (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is written like a personal reflection, personal essay, or ...

Shape-shifting puzzle similar to Rubik's Cube This article is about the puzzle. For the popular phrase, see Back to square one. This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (May 2021) (Learn how and when to remove this message) The Square-1 puzzle was sold in this shape with instructions for turning it back to a cube. This is halfway through a ver...

Pour les articles homonymes, voir Kenya (homonymie). République du Kenya(sw) Jamhuri ya Kenya (en) Republic of Kenya Drapeau du Kenya Armoiries du Kenya Devise en swahili : Harambee (« Travaillons ensemble ») Hymne en swahili : Ee Mungu Nguvu Yetu (« Ô Dieu de toute création ») Fête nationale 12 décembre · Événement commémoré Indépendance vis-à-vis du Royaume-Uni (1963) Administration Forme de l'État République Pr�...

L'occhio nel cieloTitolo originaleEye in the Sky Altri titoliOcchio nel cielo AutorePhilip K. Dick 1ª ed. originale1957 1ª ed. italiana1959 Genereromanzo Sottogenerefantascienza Lingua originaleinglese Modifica dati su Wikidata · Manuale L'occhio nel cielo o Occhio nel cielo (Eye in the Sky) è un romanzo di fantascienza scritto nel 1957 da Philip K. Dick. Indice 1 Trama 2 Temi ricorrenti 3 Bibliografia 3.1 Bibliografia critica 3.2 Edizioni 4 Collegamenti esterni Trama La storia ...

Pour les articles homonymes, voir Aru. Fabio AruFabio Aru lors du Tour d'Espagne 2015.InformationsSurnom Il cavaliere dei quatro mori (Le Chevalier des quatre Maures)Naissance 3 juillet 1990 (34 ans)San Gavino MonrealeNationalité italienneSpécialité GrimpeurDistinction Collier d'or du Mérite sportifÉquipes amateurs 2009Palazzago Elledent Rad Logistica2010Palazzago Elledent Rad2011Palazzago Elledent Rad Logistica-MCipollini01.2012-07.2012[n 1]Palazzago Elledent Rad LogisticaÉquipes...

Matteo VillaniNazionalità Italia Altezza181 cm Peso62 kg Atletica leggera Specialità3000 metri siepi Società Ballotta Camp Record 3000 siepi 8'2173 (2008) CarrieraSocietà 1998-2004 La Fratellanza 18742004-2012 Carabinieri2013-2014 La Fratellanza 18742015- Ballotta Camp Nazionale 2006- Italia7 Statistiche aggiornate al 20 giugno 2010 Modifica dati su Wikidata · Manuale Matteo Villani (San Secondo Parmense, 29 agosto 1982) è un siepista italiano, due volte campione ital...

Short-term state of the atmosphere This article is about the atmospheric process. For the geological process, see Weathering. For other uses, see Weather (disambiguation) and Weather systems (disambiguation). Fair weather redirects here. For other uses, see Fairweather (disambiguation). Part of a series onWeather Temperate and polar seasons Winter Spring Summer Autumn Tropical seasons Dry season Harmattan Wet season Storms Cloud Cumulonimbus cloud Arcus cloud Downburst Microburst Heat burst D...
