| Distribución t de Student |
|---|
![]()
Función de densidá de probabilidá |
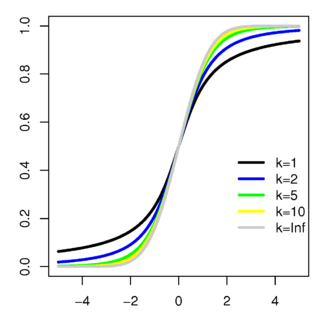
Función de distribución de probabilidá |
| Parámetros |
 graos de llibertá (real) graos de llibertá (real) |
|---|
| Función de densidá (pdf) |
 |
|---|
| Función de distribución (cdf) |
![{\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02732e546784af1fb16d0dc1bb65dd743e2284ad) onde onde  ye la función hipergeométrica ye la función hipergeométrica |
|---|
| Media |
 pa pa  , indefinida pa otros valores mediana = , indefinida pa otros valores mediana =  |
|---|
| Moda |
 |
|---|
| Varianza |
 pa pa  , indefinida pa otros valores , indefinida pa otros valores |
|---|
| Coeficiente de simetría |
 pa pa  |
|---|
| Curtosis |
 pa pa  |
|---|
| Entropía |
![{\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\log {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10a24f6de51905e2cbc5b0d4cdae5b1fa7049352)
 : función digamma, * : función digamma, *
 : función beta : función beta |
|---|
| Función xeneradora de momentos (mgf) |
(Non definida) |
|---|
| [editar datos en Wikidata] |
En probabilidá y estadística, la distribución t (de Student) ye una distribución de probabilidá que surde del problema d'envalorar la media d'una población de normal distribuyida cuando'l tamañu de la muestra ye pequeñu.
Apaez de manera natural al realizar la prueba t de Student pa la determinación de les diferencies ente dos medies muestrales y pa la construcción del intervalu d'enfotu pa la diferencia ente les medies de dos poblaciones cuando se desconoz la esviación típica d'una población y ésta ten de ser envalorada a partir de los datos d'una muestra.
Carauterización
La distribución t de Student ye la distribución de probabilidá del cociente

onde
Si μ ye una constante non nula, el cociente  ye una variable aleatoria que sigue la distribución t de Student non central con parámetru de non-centralidad
ye una variable aleatoria que sigue la distribución t de Student non central con parámetru de non-centralidad  .
.
Apaición y especificaciones de la distribución t de Student
Supongamos que X1,..., Xn son variables aleatories independientes distribuyíes de normal, con media μ y varianza σ2.
Sía

la media muestral. Entós

sigue una distribución normal de media 0 y varianza 1.
Sicasí, yá que la esviación estándar non siempres ye conocida de mano, Gosset estudió un cociente rellacionáu,


ye la cuasivarianza muestral y demostró que la función de densidá de T ye

onde  ye igual a n − 1.
ye igual a n − 1.
La distribución de T llámase agora la distribución-t de Student.
El parámetru  representa'l númberu de graos de llibertá. La distribución depende de
representa'l númberu de graos de llibertá. La distribución depende de  , pero non de
, pero non de  o
o  , lo cual ye bien importante na práutica.
, lo cual ye bien importante na práutica.
Intervalos d'enfotu derivaos de la distribución t de Student
El procedimientu pal cálculu del intervalu d'enfotu basáu na t de Student consiste n'envalorar la esviación típica de los datos S y calcular l'error estándar de la media:  , siendo entós l'intervalu d'enfotu pa la media:
, siendo entós l'intervalu d'enfotu pa la media:  .
.
Ye esta resultancia'l que s'utiliza nel test de Student: yá que la diferencia de les medies de muestres de dos distribuciones normales distribúyese tamién de normal, la distribución t puede usase pa esaminar si esa diferencia puede razonablemente suponese igual a cero.
Pa efeutos práuticos el valor esperáu y la varianza son:
 y
y  pa
pa 
Historia
La distribución de Student foi descrita en 1908 por William Sealy Gosset. Gosset trabayaba nuna fábrica de cerveza, Guinness, que prohibía a los sos emplegaos la publicación d'artículos científicos por cuenta de un espardimientu previu de secretos industriales. D'ende que Gosset publicara les sos resultaos sol seudónimu de Student.[1]
Distribución t de Student non estandarizada
La distribución t puede xeneralizase a 3 parámetros, introduciendo un parámero locacional  y otru d'escala
y otru d'escala  . La resultancia ye una distribución t de Student non estandarizada que la so densidá ta definida por:[2]
. La resultancia ye una distribución t de Student non estandarizada que la so densidá ta definida por:[2]

Equivalentemente, puede escribise en términos de  (correspondiente a la varianza en cuenta de a la esviación estándar):
(correspondiente a la varianza en cuenta de a la esviación estándar):

Otres propiedaes d'esta versión de la distribución t son:[2]

Referencies
- ↑ Walpole, Roland; Myers, Raymond y Ye, Keying (2002). Probability and Statistics for Engineers and Scientists. Pearson Education.
- ↑ 2,0 2,1 Jackman, Simon (2009). Bayesian Analysis for the Social Sciences. Wiley.
Enllaces esternos