Ó”ĖÓ”«Ó”żÓ”▓Ó¦ĆÓ”»Ó”╝ Ó”£Ó¦ŹÓ”»Ó”ŠÓ”«Ó”┐Ó”żÓ”┐Ó¦░ Ó”ŁÓ”ŠÓ”ĘÓ”ŠÓ”ż Ó”żÓ”┐Ó”©Ó”┐Ó”¤Ó”Š Ó”¼Ó”ŠÓ”╣Ó¦ü Ó”¼Ó”┐Ó”ČÓ”┐Ó”ĘÓ¦ŹÓ”¤ Ó”ĖÓ¦ĆÓ”«Ó”ŠÓ”¼Ó””Ó¦ŹÓ”¦ Ó”ĢÓ¦ŹÓ”ĘÓ¦ćÓ”żÓ¦ŹÓ¦░Ó”ĢÓ¦ć Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ Ó”¼Ó¦ŗÓ”▓Ó”Š Ó”╣Ó”»Ó”╝Óźż Ó””Ó¦ŹÓ”¼Ó”┐-Ó”«Ó”ŠÓ”żÓ¦ŹÓ¦░Ó”┐Ó”Ģ Ó”ģÓ”éÓ”ĢÓ”ż Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”żÓ”┐Ó”©Ó”┐Ó”¤Ó”Š Ó”ĢÓ¦ŗÓ”ŻÓ¦░ Ó”ĖÓ”«Ó”ĘÓ¦ŹÓ”¤Ó”┐ Ó¦¦Ó¦«Ó¦”┬░ Ó”¼Ó”Š Ó””Ó¦üÓ”ć Ó”ĖÓ”«Ó”ĢÓ¦ŗÓ”ŻÓźż Ó”ÅÓ”¤Ó”Š Ó”ĖÓ”«Ó”»Ó”╝Ó”ż Ó”ĢÓ¦ćÓ¦▒Ó”▓ Ó”ćÓ”ēÓ”ĢÓ¦ŹÓ”▓Ó”┐Ó”ĪÓ¦ĆÓ”»Ó”╝ Ó”£Ó¦ŹÓ”»Ó”ŠÓ”«Ó”┐Ó”żÓ”┐Ó”żÓ¦ćÓ”ć Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”¼Ó”┐Ó”ĘÓ”»Ó”╝Ó¦ć Ó”åÓ”▓Ó¦ŗÓ”ÜÓ”©Ó”Š Ó”ĢÓ¦░Ó”Š Ó”╣Ó¦łÓ”øÓ”┐Ó”▓Óźż Ó”ĢÓ”┐Ó”©Ó¦ŹÓ”żÓ¦ü Ó”©Ó”┐Ó”ĢÓ¦ŗÓ”▓Ó”ŠÓ”ć Ó”▓Ó¦ŗÓ”¼Ó”ŠÓ”ÜÓ¦ćÓ”ŁÓ¦ŹŌĆīÓ”ĖÓ¦ŹÓ”ĢÓ”┐ Ó”ĖÓ”╣ Ó”ģÓ”©Ó¦ŹÓ”»Ó”ŠÓ”©Ó¦ŹÓ”» Ó”£Ó¦ŹÓ”»Ó”ŠÓ”«Ó”┐Ó”żÓ”┐ Ó”¼Ó”┐Ó”ČÓ¦ćÓ”ĘÓ”£Ó¦ŹÓ”×Ó”ĖÓ”ĢÓ”▓Ó¦░ Ó”ģÓ¦▒Ó””Ó”ŠÓ”©Ó¦░ Ó”½Ó”▓Ó”ĖÓ¦ŹÓ”¼Ó¦░Ó¦éÓ”¬Ó¦ć Ó”ģÓ”ĖÓ”«Ó”żÓ”▓Ó¦ĆÓ”»Ó”╝ Ó”£Ó¦ŹÓ”»Ó”ŠÓ”«Ó”┐Ó”żÓ”┐Ó”¤Ó¦ŗ Ó”¼Ó¦░Ó¦ŹÓ”żÓ”«Ó”ŠÓ”©Ó¦ć Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”¼Ó”┐Ó”ĘÓ”»Ó”╝Ó¦ć Ó”åÓ”▓Ó¦ŗÓ”ÜÓ”©Ó”Š Ó”ĢÓ¦░Ó”Š Ó”╣Ó”»Ó”╝Óźż Ó”ÅÓ”ć Ó”¦Ó¦░Ó”ŻÓ¦░ Ó”ģÓ”éÓ”ĢÓ”ż Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”żÓ”┐Ó”©Ó”┐Ó”¤Ó”Š Ó”ĢÓ¦ŗÓ”ŻÓ¦░ Ó”ĖÓ”«Ó”ĘÓ¦ŹÓ”¤Ó”┐ Ó””Ó¦üÓ”ć Ó”ĖÓ”«Ó”ĢÓ¦ŗÓ”Ż Ó”©Ó”╣Ó”»Ó”╝Óźż Ó”ģÓ”źÓ”Ü Ó”ćÓ”ēÓ”ĢÓ¦ŹÓ”▓Ó”┐Ó”ĪÓ¦ĆÓ”»Ó”╝ Ó”£Ó¦ŹÓ”»Ó”ŠÓ”«Ó”┐Ó”żÓ”┐Ó¦░ Ó”«Ó¦éÓ”▓ Ó”ŁÓ”┐Ó”żÓ¦ŹÓ”żÓ”┐Ó”żÓ¦ćÓ”ć Ó”ÅÓ”ć Ó”¦Ó”ŠÓ¦░Ó”ŻÓ”ŠÓ”¤Ó”┐ Ó”ŚÓ”óÓ”╝ Ó”▓Ó¦łÓ”øÓ¦ćÓźż
Ó”¬Ó¦ŹÓ¦░Ó”ĢÓ”ŠÓ¦░Ó”ŁÓ¦ćÓ””
Ó”¼Ó”ŠÓ”╣Ó¦üÓ¦░ Ó””Ó¦łÓ¦░Ó¦ŹÓ”śÓ¦ŹÓ”»Ó¦░ Ó”ŁÓ”┐Ó”żÓ¦ŹÓ”żÓ”┐Ó”ż
Ó”¼Ó”ŠÓ”╣Ó¦üÓ¦░ Ó””Ó¦łÓ¦░Ó¦ŹÓ”śÓ¦ŹÓ”»Ó¦░ Ó”ŁÓ”┐Ó”żÓ¦ŹÓ”żÓ”┐Ó”ż Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ Ó”żÓ”┐Ó”©Ó”┐ Ó”¬Ó¦ŹÓ¦░Ó”ĢÓ”ŠÓ¦░Ó¦░ Ó”╣ŌĆÖÓ”¼ Ó”¬Ó”ŠÓ¦░Ó¦ćÓźż Ó”»Ó¦ćÓ”©Ó¦ć -
- Ó”ĖÓ”«Ó”¼Ó”ŠÓ”╣Ó¦ü Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ - Ó”»Ó”ŠÓ¦░ Ó”żÓ”┐Ó”©Ó”┐Ó”¤Ó”┐ Ó”¼Ó”ŠÓ”╣Ó¦üÓ¦░ Ó””Ó¦łÓ¦░Ó¦ŹÓ”śÓ¦ŹÓ”» Ó”ĖÓ”«Ó”ŠÓ”©Óźż (Ó”ĖÓ”«Ó”¼Ó”ŠÓ”╣Ó¦ü Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”ĢÓ¦ŹÓ”ĘÓ¦ćÓ”żÓ¦ŹÓ¦░Ó”ż Ó”¬Ó¦ŹÓ¦░Ó”żÓ”┐Ó”¤Ó¦ŗ Ó”ĢÓ¦ŗÓ”ŻÓ¦░ Ó”«Ó”ŠÓ”© Ó¦¼Ó¦”┬░ Ó”╣Ó”»Ó”╝Óźż
- Ó”ĖÓ”«Ó””Ó¦ŹÓ”¼Ó”┐Ó”¼Ó”ŠÓ”╣Ó¦ü Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ - Ó”»Ó”ŠÓ¦░ Ó”»Ó”┐Ó”ĢÓ¦ŗÓ”©Ó¦ŗ Ó””Ó¦üÓ”ć Ó”¼Ó”ŠÓ”╣Ó¦üÓ¦░ Ó””Ó¦łÓ¦░Ó¦ŹÓ”śÓ¦ŹÓ”» Ó”ĖÓ”«Ó”ŠÓ”©Óźż (Ó”ĖÓ”«Ó””Ó¦ŹÓ”¼Ó”┐Ó”¼Ó”ŠÓ”╣Ó¦ü Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”ČÓ¦ĆÓ¦░Ó¦ŹÓ”ĘÓ”ĢÓ¦ŗÓ”Ż Ó¦»Ó¦”┬░ Ó”╣ŌĆÖÓ”▓Ó¦ć Ó”åÓ”© Ó”ĖÓ”«Ó”ŠÓ”© Ó””Ó¦üÓ”ćÓ”¤Ó”┐ Ó”¼Ó”┐Ó”¬Ó¦░Ó¦ĆÓ”ż Ó”ĢÓ¦ŗÓ”Ż Ó¦¬Ó¦½┬░Ó”ĢÓ¦ł Ó”╣ŌĆÖÓ”¼Óźż )
- Ó”¼Ó”┐Ó”ĘÓ”«Ó”¼Ó”ŠÓ”╣Ó¦ü Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ - Ó”»Ó”ŠÓ¦░ Ó”żÓ”┐Ó”©Ó”┐Ó”¤Ó”Š Ó”¼Ó”ŠÓ”╣Ó¦üÓ¦░ Ó””Ó¦łÓ¦░Ó¦ŹÓ”śÓ¦ŹÓ”» Ó”żÓ”┐Ó”©Ó”┐ Ó”¦Ó¦░Ó”ŻÓ¦░Óźż (Ó”¼Ó”┐Ó”ĘÓ”«Ó”¼Ó”ŠÓ”╣Ó¦ü Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”żÓ”┐Ó”©Ó”┐Ó”ōÓ”¤Ó”Š Ó”ĢÓ¦ŗÓ”ŻÓ¦ćÓ”ć Ó”ÅÓ”¤Ó”Š Ó”åÓ”©Ó”¤Ó¦ŗÓ¦░ Ó”¬Ó¦░Ó”Š Ó”¬Ó¦āÓ”źÓ”Ģ Ó”╣Ó”»Ó”╝Óźż
 |
 |
 |
| Ó”ĖÓ”«Ó”¼Ó”ŠÓ”╣Ó¦ü | Ó”ĖÓ”«Ó””Ó¦ŹÓ”¼Ó”┐Ó”¼Ó”ŠÓ”╣Ó¦ü | Ó”¼Ó”┐Ó”ĘÓ”«Ó”¼Ó”ŠÓ”╣Ó¦ü |
Ó”ĢÓ¦ŗÓ”ŻÓ¦░ Ó”ŁÓ”┐Ó”żÓ¦ŹÓ”żÓ”┐Ó”ż Ó”ĢÓ¦░Ó”Š Ó”¼Ó”┐Ó”ŁÓ”ŠÓ”£Ó”©
Ó”ĢÓ¦ŗÓ”ŻÓ¦░ Ó”ŁÓ”┐Ó”żÓ¦ŹÓ”żÓ”┐Ó”ż Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ Ó”żÓ”┐Ó”©Ó”┐ Ó”¬Ó¦ŹÓ¦░Ó”ĢÓ”ŠÓ¦░Ó¦░ Ó”╣ŌĆÖÓ”¼ Ó”¬Ó”ŠÓ¦░Ó¦ć -
- Ó”ĖÓ”«Ó”ĢÓ¦ŗÓ”ŻÓ¦Ć Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ - Ó”»Ó”ŠÓ¦░ Ó”»Ó”┐Ó”ĢÓ¦ŗÓ”©Ó¦ŗ Ó”ÅÓ”¤Ó”┐ Ó”ĢÓ¦ŗÓ”Ż Ó¦¦ Ó”ĖÓ”«Ó”ĢÓ¦ŗÓ”Ż Ó”¼Ó”Š Ó¦»Ó¦”┬░Ó¦░ Ó”ĖÓ”«Ó”ŠÓ”©Óźż
- Ó”ĖÓ¦éÓ”ĢÓ¦ŹÓ”ĘÓ¦ŹÓ”ŻÓ”ĢÓ¦ŗÓ”ŻÓ¦Ć Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ - Ó”»Ó”ŠÓ¦░ Ó”żÓ”┐Ó”©Ó”┐Ó”¤Ó”┐ Ó”ĢÓ¦ŗÓ”ŻÓ¦ćÓ”ć Ó”ĖÓ¦éÓ”ĢÓ¦ŹÓ”ĘÓ¦ŹÓ”ŻÓ”ĢÓ¦ŗÓ”Ż
- Ó”ĖÓ¦ŹÓ”źÓ¦éÓ”▓Ó”ĢÓ¦ŗÓ”ŻÓ¦Ć Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ - Ó”»Ó”ŠÓ¦░ Ó”»Ó”┐Ó”ĢÓ¦ŗÓ”©Ó¦ŗ Ó”ÅÓ”¤Ó”┐ Ó”ĢÓ¦ŗÓ”Ż Ó”ĖÓ¦ŹÓ”źÓ¦éÓ”▓Ó”ĢÓ¦ŗÓ”ŻÓźż
 |
 |
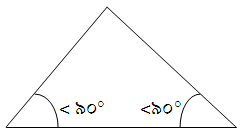 |
| Ó”ĖÓ”«Ó”ĢÓ¦ŗÓ”ŻÓ¦Ć | Ó”ĖÓ¦ŹÓ”źÓ¦éÓ”▓Ó”ĢÓ¦ŗÓ”ŻÓ¦Ć | Ó”ĖÓ¦éÓ”ĢÓ¦ŹÓ”ĘÓ¦ŹÓ”ŻÓ”ĢÓ¦ŗÓ”ŻÓ¦Ć |
Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”ĖÓ”ŠÓ””Ó¦āÓ”ČÓ¦ŹÓ”»Ó”żÓ”Š
Ó””Ó¦üÓ”¤Ó”Š Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ Ó”ĖÓ””Ó¦āÓ”Č Ó”╣'Ó”¼ Ó”»Ó””Ó”┐Ó”╣Ó¦ć- i) Ó”ĖÓ”┐Ó”╣Ó”üÓ”żÓ¦░ Ó”ģÓ”©Ó¦üÓ¦░Ó¦éÓ”¬ Ó”ĢÓ¦ŗÓ”ŻÓ”¼Ó¦ŗÓ¦░ Ó”ĖÓ”«Ó”ŠÓ”© Ó”åÓ¦░Ó¦ü ii) Ó”ĖÓ”┐Ó”╣Ó”üÓ”żÓ¦░ Ó”ģÓ”©Ó¦üÓ¦░Ó¦éÓ”¬ Ó”¼Ó”ŠÓ”╣Ó¦üÓ”¼Ó¦ŗÓ¦░ Ó”ÅÓ”ĢÓ¦ć Ó”ģÓ”©Ó¦üÓ”¬Ó”ŠÓ”żÓ”ż Ó”źÓ”ŠÓ”ĢÓ¦ćÓźż Ó”»Ó””Ó”┐ Ó””Ó¦üÓ”¤Ó”Š Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”ģÓ”©Ó¦üÓ¦░Ó¦éÓ”¬ Ó”ĢÓ¦ŗÓ”ŻÓ”¼Ó”┐Ó”▓Ó”ŠÓ”Ģ Ó”ĖÓ”«Ó”ŠÓ”© Ó”żÓ¦ćÓ”©Ó¦ŹÓ”żÓ¦ć Ó”ĖÓ”┐Ó”╣Ó”üÓ”ż Ó”ĖÓ”«Ó”ŠÓ”© Ó”ĢÓ¦ŗÓ”ŻÓ¦Ć Ó”¼Ó”Š Ó”ĖÓ”«Ó”ĢÓ¦īÓ”ŻÓ¦ĆÓ”Ģ Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£ Ó”¼Ó¦ŗÓ”▓Ó¦ćÓźż Ó”¼Ó”┐Ó”¢Ó¦ŹÓ”»Ó”ŠÓ”ż Ó”ŚÓ¦ŹÓ¦░Ó¦ĆÓ”Ģ Ó”ŚÓ”ŻÓ”┐Ó”żÓ”£Ó¦ŹÓ”× Ó”źÓ¦ćÓ”▓Ó”øÓ¦ć Ó””Ó¦üÓ”¤Ó”Š Ó”ĖÓ”«Ó”ĢÓ¦ŗÓ”ŻÓ¦Ć Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”ĢÓ¦ŹÓ”ĘÓ¦ćÓ”żÓ¦ŹÓ¦░Ó”ż Ó”ÅÓ”¤Ó”Š Ó”ŚÓ¦üÓ¦░Ó¦üÓ”żÓ¦ŹÓ”¼Ó”¬Ó¦éÓ¦░Ó¦ŹÓ”Ż Ó”ĖÓ”żÓ¦ŹÓ”» Ó”ēÓ”▓Ó¦ŹÓ”▓Ó¦ćÓ”¢ Ó”ĢÓ¦░Ó”┐Ó”øÓ”┐Ó”▓Óźż Ó”ĖÓ¦ćÓ”ćÓ”¤Ó¦ŗ Ó”╣'Ó”▓- Ó””Ó¦üÓ”¤Ó”Š Ó”ĖÓ”«Ó”ŠÓ”©Ó”ĢÓ¦ŗÓ”ŻÓ¦Ć Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”»Ó”┐Ó”ĢÓ¦ŗÓ”©Ó¦ŗ Ó””Ó¦üÓ”¤Ó”Š Ó”ģÓ”©Ó¦üÓ¦░Ó¦éÓ”¬ Ó”¼Ó”ŠÓ”╣Ó¦üÓ¦░ Ó”ģÓ”©Ó¦üÓ”¬Ó”ŠÓ”ż Ó”ĖÓ””Ó”ŠÓ”»Ó”╝ Ó”ÅÓ”ĢÓ¦ćÓźż Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”ĖÓ””Ó¦āÓ”ČÓ”żÓ”Š Ó”¼Ó¦üÓ”£Ó”┐Ó”¼Ó”▓Ó¦ł '~' Ó”¬Ó¦ŹÓ¦░Ó”żÓ¦ĆÓ”Ģ Ó”¼Ó¦ŹÓ”»Ó¦▒Ó”╣Ó”ŠÓ¦░ Ó”ĢÓ¦░Ó”Š Ó”╣Ó”»Ó”╝Óźż Ó””Ó¦üÓ”¤Ó”Š Ó”ĖÓ””Ó¦āÓ”Č Ó”żÓ¦ŹÓ¦░Ó”┐Ó”ŁÓ¦üÓ”£Ó¦░ Ó”ĢÓ”ŠÓ”▓Ó”┐Ó¦░ Ó”ģÓ”©Ó¦üÓ”¬Ó”ŠÓ”ż Ó”ĖÓ”┐Ó”╣Ó”üÓ”żÓ¦░ Ó”ģÓ”©Ó¦üÓ¦░Ó¦éÓ”¬ Ó”¼Ó”ŠÓ”╣Ó¦üÓ¦░ Ó”ģÓ”©Ó¦üÓ”¬Ó”ŠÓ”żÓ¦░ Ó”¼Ó¦░Ó¦ŹÓ”ŚÓ¦░ Ó”ĖÓ”«Ó”ŠÓ”©Óźż
Ó”żÓ”źÓ¦ŹÓ”» Ó”ĖÓ”éÓ”ŚÓ¦ŹÓ¦░Ó”╣
Ó”¼Ó”ŠÓ”╣Ó¦ŹÓ”»Ó”┐Ó”Ģ Ó”ĖÓ”éÓ”»Ó¦ŗÓ”Ś