Read other articles:

MuncangKecamatanNegara IndonesiaProvinsiBantenKabupatenLebakPemerintahan • Camat-Populasi • Total- jiwaKode Kemendagri36.02.05 Kode BPS3602110 Luas- km²Desa/kelurahan- Kantor Kecamatan Muncang Muncang adalah sebuah kecamatan di Kabupaten Lebak, Provinsi Banten, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Administrasi Pemerintahan, dan Pulau tahun 2021 (Indonesia)...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Dendragama schneideri TaksonomiKerajaanAnimaliaFilumChordataKelasReptiliaOrdoSquamataFamiliAgamidaeGenusDendragamaSpesiesDendragama schneideri Ahl, 1926 lbs Dendragama schneideri, atau agama pohon Schneider, adalah sebuah spesies kadal dalam keluarga ...

Peta Lokasi Kabupaten Ogan Ilir di Sumatera Selatan Berikut adalah daftar kecamatan dan kelurahan/desa di Kabupaten Ogan Ilir, Sumatera Selatan, Indonesia. Kabupaten Ogan Ilir memiliki 16 kecamatan, 14 kelurahan dan 227 desa (dari total 236 kecamatan, 386 kelurahan dan 2.853 desa di seluruh Sumatera Selatan). Pada tahun 2017, jumlah penduduknya sebesar 410.529 jiwa dengan luas wilayahnya 2.666,09 km² dan sebaran penduduk 154 jiwa/km².[1][2] Daftar kecamatan dan kelurahan di ...

Peterseli adalah sebuah contoh umum dari tumbuhan dwimusim. Tumbuhan dwimusim adalah sebuah tumbuhan berbunga yang membutuhkan waktu dua tahun untuk menyelesaikan siklus kehidupan biologisnya.[1][2] Pada tahun pertama, tumbuhan tersebut menjalani pertumbuhan primer, dimana daun, batang dan akarnya (struktur vegetatif) berkembang. Referensi ^ Annual, Perennial, Biennial?. Texas Cooperative Extension. Diarsipkan dari versi asli tanggal 14 August 2012. Diakses tanggal 31 August 2...

Untuk hal lainnya, lihat Batu (disambiguasi). Batuan yang terletak di taman Garden of the Gods di Colorado Springs, Colorado, Amerika Serikat. Batu adalah benda alam yang tersusun atas kumpulan mineral penyusun kerak bumi yang menyatu secara padat maupun berserakan. Pembentukan batu merupakan hasil proses alam. Di dalam batu dapat terkandung satu atau beberapa jenis mineral.[1] Batu dapat terbentuk melalui proses kristalisasi magma, sedimentasi, maupun metamorfisme. Dari proses pemben...

نادي فينر تأسس عام 1883  البلد النمسا  الموقع الرسمي الموقع الرسمي  تعديل مصدري - تعديل   نادي فينر الرياضي (بالألمانية: Wiener Sportklub) نادي كرة قدم نمساوي يلعب في دوري الدرجة الثالثة.[1][2] تم تأسيس النادي في سنة 1883. مراجع ^ معلومات عن نادي فينر على موقع viaf.org. viaf.org. م�...

American politician A. P. Lutali2nd & 4th Governor of American SamoaIn officeJanuary 3, 1993 – January 3, 1997LieutenantTauese SuniaPreceded byPeter Tali ColemanSucceeded byTauese SuniaIn officeJanuary 3, 1985 – January 2, 1989LieutenantEni FaleomavaegaPreceded byPeter Tali ColemanSucceeded byPeter Tali ColemanDelegate at-large of American SamoaIn officeJanuary 3, 1975 – January 3, 1979Preceded byA. U. FuimaonoSucceeded byFofō Sunia Personal detailsBornAi...

American politician (1816–1894) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: James L. Alcorn – news · newspapers · books · scholar · JSTOR (July 2021) (Learn how and when to remove this template message) James L. AlcornUnited States Senatorfrom MississippiIn officeDecember 1, 1871 – March 3, 1877Prece...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Final Piala Raja Spanyol 2000TurnamenPiala Raja Spanyol 1999–2000 Espanyol Atlético Madrid 2 1 Tanggal27 Mei 2000StadionStadion Mestalla, ValenciaWasitAntonio Jesús López NietoPenonton55.000CuacaSedikit berawan21 °C (70 °F)← 1999 2001 → Final Piala Raja Spanyol 2000 adalah pertandingan final ke-96 dari turnamen sepak bola Piala Raja Spanyol untuk menentukan juara musim 1999–2000. Pertandingan ini diikuti oleh Espanyol dan Atlético Madrid dan diselenggarakan pad...

Logo resmi St George Park (SGP) adalah pusat sepak bola nasional Inggris milik Football Association yang berdiri di lahan seluas 330 hektare (130 ha) di Burton upon Trent, Staffordshire.[1] Tujuan dari pusat ini adalah untuk menjadi dasar untuk semua pembinaan dan pengembangan yang dilakukan oleh FA, dan tempat berlatih untuk semua tim nasional sepak bola Inggris. Referensi ^ Are club and country now working together?. BBC Sport. Diakses tanggal 2 February 2012.  Teks Football ak...

This article is about the Dutch channel. For the Polish Comedy Central Family, see Comedy Central Family (Polish TV channel). Television channel Comedy Central FamilyCountryNetherlandsBroadcast areaNetherlandsNetworkComedy CentralProgrammingPicture format576i 16:9 (SDTV)OwnershipOwnerParamount International NetworksEndemol NederlandHistoryLaunched1 October 2008; 15 years ago (2008-10-01)Closed31 May 2018; 5 years ago (2018-05-31)AvailabilityStreaming mediaZ...

本條目存在以下問題，請協助改善本條目或在討論頁針對議題發表看法。 此條目需要擴充。 (2013年1月1日)请協助改善这篇條目，更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 此條目需要补充更多来源。 (2013年1月1日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。致使用者：请搜索一下条目的...

شبه جزيرة ريباتشي     الإحداثيات 69°42′N 32°36′E / 69.7°N 32.6°E / 69.7; 32.6   تقسيم إداري  البلد روسيا[1]  التقسيم الأعلى أوبلاست مورمانسك  رمز جيونيمز 500038  تعديل مصدري - تعديل   شبه جزيرة ريباتشي (بالروسية: полуо́стров Рыба́чий؛ بلغة سامي الشمالية: Gieh...

العلاقات الألبانية النمساوية ألبانيا النمسا   ألبانيا   النمسا تعديل مصدري - تعديل   العلاقات الألبانية النمساوية هي العلاقات الثنائية التي تجمع بين ألبانيا والنمسا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقا...

Part of a series on theCulture of Scotland History Timeline Prehistoric Roman times Middle Ages Early Middle Ages Kingdom High Middle Ages Davidian Revolution Wars of Independence Late Middle Ages Renaissance Early modern Reformation Colonisation of the Americas Glorious Revolution 1707 Acts of Union Jacobitism Enlightenment Lowland Clearances Highland Clearances Industrial Revolution Romanticism Modern People Languages Scottish Gaelic Broad Scots Scottish English Pictish Norn Traditions Clo...

Kingdom in the north of early Anglo-Saxon Britain For other uses, see Deira (disambiguation). For the district in Dubai, see Deira, Dubai. Kingdom of Deirac. 450–654CapitalYorkCommon languagesOld English, Common BrittonicGovernmentMonarchyHistorical eraEarly Medieval• Established c. 450• Shared crown with Bernicia 604• merged with Bernicia 654 Preceded by Succeeded by Sub-Roman Britain Parisi (tribe) Northumbria Deira (/ˈdaɪrə, ˈdɛərə/ DY-rə, DAIR-ə;[1...

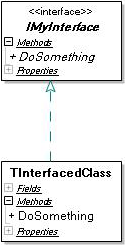
Изображение интерфейса и реализующего его класса в «Together». COM-интерфе́йс (от COM — англ. Component Object Model и англ. interface — взаимодействие) — набор абстрактных функций и свойств, через который программы взаимодействует с COM-компонентом. Состав этого набора объявляется незав...

六条天皇 『歴代尊影』第79代天皇 在位期間1165年8月3日 - 1168年3月30日永万元年6月25日 - 仁安3年2月19日即位礼 1165年9月4日（永万元年7月27日）大嘗祭 1166年12月9日（仁安元年11月15日）元号 永万仁安時代 平安時代先代 二条天皇次代 高倉天皇誕生 1164年12月28日（長寛2年11月14日）崩御 1176年8月23日（安元2年7月17日）東山第大喪儀 1176年8月28日（安元2年7月22日）陵所 清閑寺陵追...

Argument for the existence of God Part of a series onRené Descartes Philosophy Cartesianism Rationalism Foundationalism Mechanism Doubt and certainty Dream argument Cogito, ergo sum Evil demon Trademark argument Causal adequacy principle Mind–body dichotomy Analytic geometry Coordinate system Cartesian circle Folium Rule of signs Cartesian diver Balloonist theory Wax argument Res cogitans Res extensa Works Rules for the Direction of the Mind The Search for Truth The World Discourse on the ...