Read other articles:

Dietrich BonhoefferLahir(1906-02-04)4 Februari 1906Breslau, Schlesien, Prusia, Jerman(sekarang Wrocław, Polandia)Meninggal9 April 1945(1945-04-09) (umur 39)Flossenbürg, Bayern, JermanSebab meninggalEksekusi dengan cara digantungPendidikanStaatsexamen (Tübingen), Doktor Teologi (Berlin), Privatdozent (Berlin)GerejaPersatuan Gereja-gereja Prussia (1906–1933)Gereja yang Mengaku (1933–1945)Karya tulisPenulis beberapa buku dan artikel (lihat di bawah)JemaatJemaat Gereja Zion, Ber...

Masjid BirgiBirgi CamiiAgamaAfiliasiIslam – SunniProvinsiİzmirLokasiLokasiBirgiNegara TurkiArsitekturTipeMasjidGaya arsitekturTurki dengan sedikit sentuhan arsitektur SeljukDidirikan1311Menara1 Masjid Birgi (bahasa Turki: Birgi Camii), secara resmi bernama Masjid Raya Birgi (bahasa Turki: Birgi Ulucamii) atau lebih dikenal dengan Masjid Aydınoğlu Mehmed Bey (bahasa Turki: Aydınoğlu Mehmet Bey Camii) adalah sebuah masjid bersejarah peninggalan Dinasti Seljuk pada abad ke-14 yang be...

Romawi Kuno Artikel ini adalah bagian dari seri Politik dan KetatanegaraanRomawi Kuno Zaman Kerajaan Romawi753–509 SM Republik Romawi509–27 SM Kekaisaran Romawi27 SM – 395 M Principatus Dominatus Wilayah Barat395–476 M Wilayah Timur395–1453 M Lini Masa Konstitusi Romawi Konstitusi Zaman Kerajaan Konstitusi Zaman Republik Konstitusi Zaman Kekaisaran Konstitusi Akhir Zaman Kekaisaran Senatus Sidang Legislatif Magistratus Eksekutif Preseden dan Hukum Hukum Romawi Ius Imperium Mos Maio...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Pemangku kepentingan – berita · surat kabar · buku · cendekiawan · JSTOR Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Stakeholder (corporate) di en.wikipedia.org. Isinya masih belum ...

العلاقات الأنغولية النمساوية أنغولا النمسا   أنغولا   النمسا تعديل مصدري - تعديل   العلاقات الأنغولية النمساوية هي العلاقات الثنائية التي تجمع بين أنغولا والنمسا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة...

Election in Michigan Main article: 1956 United States presidential election 1956 United States presidential election in Michigan ← 1952 November 6, 1956 1960 → All 20 Michigan votes to the Electoral CollegeTurnout67.9% [1]   Nominee Dwight D. Eisenhower Adlai Stevenson Party Republican Democratic Home state Pennsylvania[2][3] Illinois Running mate Richard Nixon Estes Kefauver Electoral vote 20 0 Popular vote 1,713,647 1,35...

Lintas JakartaIkhtisarJenisJalur kereta api lintas utamaSistemJalur kereta api perkotaanStatusBeroperasiStasiun26 (lintas sekitar Jakarta)OperasiDibukaBervariasi, lihat di bawah.Pemilik Direktorat Jenderal Perkeretaapian PT Kereta Api Indonesia (Persero) (pemilik aset tanah dan bangunan) OperatorKereta Api Indonesia KAI Commuter[a] Daerah Operasi I Jakarta Terminus Jakarta Stasiun Gambir Stasiun Pasar Senen Stasiun Jakarta Kota Stasiun Jatinegara KAI Logistik Stasiun Jakarta Gudang St...

Primary sources of renewable energy in South Africa are solar, wind, hydroelectric, and biomass. Pictured here are wind turbines in Darling, Cape Province. Renewable energy in South Africa is energy generated in South Africa from renewable resources, those that naturally replenish themselves—such as sunlight, wind, tides, waves, rain, biomass, and geothermal heat.[1] Renewable energy focuses on four core areas: electricity generation, air and water heating/cooling, transportation, ...

Hong KongSpecial Administrative RegionSecretary for Housing 房屋局局長Emblem of Hong KongIncumbentWinnie Hosince 1 July 2022Housing BureauStyleThe HonourableAppointerCentral People's Governmentnomination by Chief ExecutiveInaugural holderIan Macdonald LightbodyFormation1973; 51 years ago (1973)WebsiteHB Secretary for HousingTraditional Chinese房屋局局長Simplified Chinese房屋局局长TranscriptionsStandard MandarinHanyu PinyinFángwū Jú JúzhǎngYue: C...

Celtic version of the god Mercury Altar of Mercurius Gebrinius, Bonn Gebrinius is a local Celtic version of the god Mercury. In the 2nd century AD, an altar was set up at Bonn to honour him. The stone depicts the god in full Roman aspect, but is, nevertheless, dedicated to Mercury Gebrinius, perhaps of the name of a local divinity of the Ubii, whose cult was linked to that of the Roman god. References Dictionary of Celtic Myth and Legend. Miranda Green. Thames and Hudson Ltd. London. 1997 vte...

弗雷德里克·齊盧巴Frederick Chiluba第2任赞比亚总统任期1991年11月2日—2002年1月2日副职利维·姆瓦纳瓦萨前任肯尼思·卡翁达继任利维·姆瓦纳瓦萨 个人资料出生(1943-04-30)1943年4月30日北罗得西亚基特韦逝世2011年6月18日(2011歲—06—18)（68歲） 尚比亞卢萨卡（Lusaka）墓地 尚比亞卢萨卡使館公園總統陵園（英语：Embassy Park Presidential Burial）国籍赞比亚政党多黨民主運動（MMD）...

2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl（英文）（波兰文）2020年夏季奥林匹克运动会（東京）2021年7月23日至8月8日（受2019冠状病毒病疫情影响推迟，但仍保留原定名称）運動員206參賽項目24个大项旗手开幕式：帕维尔·科热尼奥夫斯基（游泳）和马娅·沃什乔夫斯卡（自行车）[1]闭幕式：卡罗利娜·纳亚（皮划艇）&#...

Marquesado de Villanueva de Duero Corona marquesalPrimer titular Pedro José de Rojas y ContrerasConcesión Felipe V20 de julio de 1740, Grandeza de España en 1794 por Carlos IVActual titular Fernando Ramírez de Haro y Aguirre[editar datos en Wikidata] El marquesado de Villanueva de Duero es un título nobiliario español creado el 20 de julio de 1740 por el rey Felipe V a favor de Pedro José de Rojas y Contreras.[1]​ El 26 de enero de 1790 (carta en 1794), el rey Carlos IV...

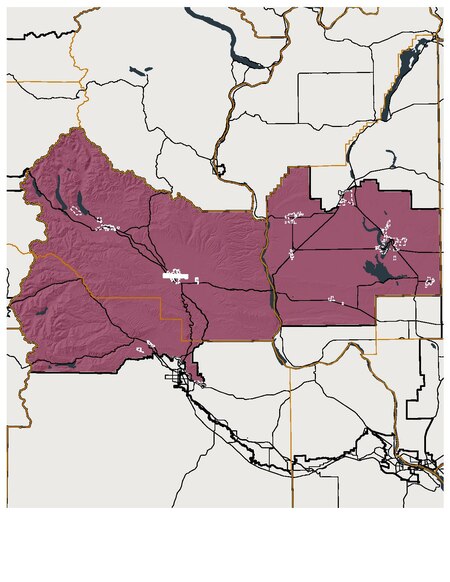
Washington's 13th legislative district map Washington's 13th legislative district is one of forty-nine districts in Washington state for representation in the state legislature. The district includes all or most of Lincoln, Grant, and Kittitas counties.[1] This rural district is represented by state senator Judy Warnick and state representatives Tom Dent (position 1) and Alex Ybarra (position 2), all Republicans.[2] See also Washington Redistricting Commission Washington Stat...

Wakil Bupati Bandung BaratPetahanaLowongsejak 13 April 2021Dibentuk2008Pejabat pertamaDrs. Ernawan Natasaputra, M.Si Berikut ini adalah daftar Wakil Bupati Bandung Barat. No Wakil Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Bupati 1 Drs. Ernawan Natasaputra, M.Si 17 Juli 2008 17 Juli 2013 1(2008) Drs. H. Abu Bakar M.Si 2 Drs. H.Yayat Turochmat Soemitra 17 Juli 2013 19 April 2018 2(2013) 3 Hengky Kurniawan 20 September 2018 13 April 2021 3(2018) Aa Umbara Sutisna Referensi Lihat Pula Daf...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Arbitrary waveform generator – news · newspapers · books · scholar · JSTOR (February 2024) (Learn how and when to remove this message) The BK Precision model 4078 Dual Channel Arbitrary Waveform Generator uses direct digital synthesis to generate waveforms up t...

This template does not require a rating on Wikipedia's content assessment scale.It is of interest to the following WikiProjects:Stub sorting This template is maintained by WikiProject Stub sorting, an attempt to bring some sort of order to Wikipedia. If you would like to participate, you can choose to improve/expand the articles containing this stub notice, or visit the project page, where you can join the project and see a list of open tasks.Stub sortingWikipedia:WikiProject Stub sortingTemp...

Election in Delaware This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 1924 United States presidential election in Delaware – news · newspapers · books · scholar · JSTOR (November 2020) Main article: 1924 United States presidential election 1924 United States presidential election in Delaware ←...

Australian basketball player For other people with the same name, see Michael Ellis (disambiguation). Mike EllisEllis in January 2023Personal informationBorn (1958-07-27) 27 July 1958 (age 65)Perth, Western AustraliaNationalityAustralianListed height183 cm (6 ft 0 in)Listed weight85 kg (187 lb)Career informationPlaying career1982–1997PositionPoint guardNumber6Coaching career1998–presentCareer historyAs player:1982–1992Perth Wildcats1993–1994Swan City Must...

American textile professional fraternity This article is about the professional fraternity with emphasis on textile arts. For the national social fraternity with a similar nickname, see Phi Kappa Psi. Phi PsiΦΨFoundedMarch 18, 1903; 121 years ago (1903-03-18)Philadelphia College of Textiles & Science, Philadelphia, Pennsylvania, U.S.TypeProfessionalAffiliationIndependentStatusActiveEmphasisTextilesScopeNationalMottoSemper ad perfectumColors  Black and   GoldF...