Read other articles:

Fast Fourier Transform algorithm The Cooley–Tukey algorithm, named after J. W. Cooley and John Tukey, is the most common fast Fourier transform (FFT) algorithm. It re-expresses the discrete Fourier transform (DFT) of an arbitrary composite size N = N 1 N 2 {\displaystyle N=N_{1}N_{2}} in terms of N1 smaller DFTs of sizes N2, recursively, to reduce the computation time to O(N log N) for highly composite N (smooth numbers). Because of the algorithm's importance, specific variants and implemen...

BawarchiPoster PromosionalSutradaraHrishikesh MukherjeeProduserHrishikesh Mukherjee,N.C. Sippy,Romu N. SippyDitulis olehTapan SinhaPemeranRajesh Khanna,Jaya Badhuri,AsraniNaratorAmitabh BachchanPenata musikMadan MohanTanggal rilis 7 Juli 1972 (1972-07-07) (India) NegaraIndiaBahasaHindi Bawarchi (Devnagari: बावर्ची, terjemahan: Tukang Masak) adalah sebuah film Hindi 1972 yang disutradarai oleh Hrishikesh Mukherjee serta dibintangi oleh Rajesh Khanna dan Jaya Badhur...

العلاقات البوليفية الفلسطينية     بوليفيا   فلسطين السفارات سفارة دولة فلسطين لدى بوليفيا   السفير : محمود العلواني (Q122039187)   العنوان : لاباز الحدود لا حدود برية مشتركة تعديل مصدري - تعديل   العلاقات البوليفية الفلسطينية هي العلاقات الدولية بي�...

Ne doit pas être confondu avec CEREMADE. CeremaHistoireFondation 1er janvier 2014Prédécesseur Centre d'études techniques de l'ÉquipementCadreSigle CeremaType Établissement public administratifForme juridique Établissement public national à caractère administratifDomaine d'activité Administration publique (tutelle) des activités économiquesSiège Bron, Métropole de LyonPays  FranceCoordonnées 45° 44′ 16″ N, 4° 55′ 39″ EOrganisationEff...

Белохвостый олень Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКласс:Мл�...

Katedral Santo Andreas, Singapura Katedral Santo Andreas (bahasa Inggris: St Andrew's Cathedral, bahasa Melayu: Katedral St Andrew, bahasa Tamil: செயிண்ட் ஆண்ட்ரூ கதீட்ரல், Hanzi: 圣安德烈座堂; Pinyin: Shèng Āndéliè Zuòtáng) adalah sebuah katedral Anglikan di Singapura. Tempat ini adalah katedral terbesar di negara tersebut. Sejarah Dirancang oleh George Dumgoole Coleman, Gereja Santo Andreas yang asli dibangun dari 1835 sampai...

Dragon Ball: The Path to PowerCoverSutradaraShigeasu YamauchiProduserKenji ShimizuSeichi HirutaKozo MorishitaKoji KanedaBerdasarkanDragon Balloleh Akira ToriyamaPemeranSee CastPenata musikAkihito TokunagaPenyuntingShinichi FukumitsuPerusahaanproduksiToei AnimationDistributorToei CompanyTanggal rilis 04 Maret 1996 (1996-03-04) (Jepang) Durasi80 menitNegaraJepangBahasaJepang Dragon Ball: The Path to Power (ドラゴンボール 最強への道, Doragon Bōru: Saikyō e no Michi; ...

Cet article est une ébauche concernant une localité écossaise. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Torphins en écossais : Tòrr Fionn Ecole primaire de Torphins Administration Pays Royaume-Uni Nation Écosse Council area Aberdeenshire Force de police Police Scotland Incendie Scottish Fire and Rescue Service Ambulance Scottish Ambulance Service Démographie Population 1 410 hab. (20...

الوحش داخل الإنسان الصنف دراما - جريمة الموضوع تخون الشابة صدفة زوجها وتتفق مع عشيقها على قتل الزوج. تاريخ الصدور 31 يناير 1980 مدة العرض 110 دقيقة البلد مصر اللغة الأصلية العربية (العامية المصرية) الطاقم المخرج أشرف فهمي الإنتاج إيجيبكو لتوزيع الأفلام - تاكفور أنطونيان. الكاتب...

Species of butterfly Graphium idaeoides Hewitson's figure (top) in Illustrations of new species of exotic butterflies Conservation status Vulnerable  (IUCN 2.3)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Papilionidae Genus: Graphium Species: G. idaeoides Binomial name Graphium idaeoidesHewitson, 1855 Subspecies Graphium idaeoides idaeoides Graphium idaeoides neergaardi (Page & Treadaway, 2...

La Región de Murcia en España. La historia de la Región de Murcia es común al desarrollo histórico del sureste de la península ibérica. Se trata de un territorio poblado desde muy antiguo debido a su situación mediterránea que le hizo testigo del paso de numerosas culturas y civilizaciones. Conserva importantes yacimientos prehistóricos, como los segundos restos humanos más antiguos de la península en la Sima de las Palomas, o la presencia de una de las culturas más desarrolladas...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) المقالة الرئيسة: فريد الأطرش اسم الفيلم بطولة قصة إخراج تاريخ العرض انتصار الشباب فريد الأطرش وأسمهان عم...

Saudi royal and military official (born 1941) Fahd bin Abdullah bin Mohammed Al SaudDeputy Minister of DefenseIn office21 April 2013 – 7 August 2013MonarchKing AbdullahMinisterSalman bin AbdulazizPreceded byKhalid bin SultanSucceeded bySalman bin Sultan Personal detailsBorn1941 (age 82–83)NationalitySaudi ArabianSpouseFahda bint Bandar bin Mohammed Al SaudChildren8Parent(s)Abdullah bin Mohammed Al Saud Noura bint Saud Al SaudAlma materUS Naval Staff and Command CollegeAw...

Casper ØyvannNazionalità Norvegia Altezza185 cm Calcio a 5 RuoloDifensore Termine carriera2020 CarrieraSquadre di club 2015-2020 Hulløy? (?) Nazionale 2018-2020 Norvegia5 (0) Calcio RuoloDifensore Squadra Molde CarrieraGiovanili  Bodø/Glimt Squadre di club1 2018-2019 Bodø/Glimt0 (0)2019→  Mjølner8 (0)2020 Tromsdalen18 (0)2021-2023 Tromsø48 (0)2023- Molde0 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di cam...

Olympic boxing tournament Featherweight boxingat the Games of the XX OlympiadVenueBoxing Hall, MunichDates27 August – 10 SeptemberCompetitors45 from 45 nationsMedalists Boris Kuznetsov  Soviet Union Philip Waruinge  Kenya Clemente Rojas  Colombia András Botos  Hungary← 19681976 → Boxing at the1972 Summer OlympicsLight flyweightmenFlyweightmenBantamweightmenFeatherweightmenLightweightmenLight welterweightmenWelterweightmenLight middleweigh...

Below is a list of the UNESCO World Heritage Sites located in upper North America. Greenland has been included here as part of North America despite its cultural and political associations with Europe. The separate List of World Heritage Sites in Central America covers the continental areas further south. Mexico leads North America hosting 35 sites, and is ranked seventh in the world. World Heritage Sites Legend Endangered and trans-border sites   † In danger   * Trans-...

この項目では、1974年の映画について説明しています。シリーズ全体については「悪魔のいけにえシリーズ」をご覧ください。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方）出典検索?: 悪魔のいけにえ – ニュース · 書籍 · スカラー&#...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Homisida internet merujuk kepada pembunuh dimana korban dan pelaku bertemu di dunia maya. Dalam beberapa kasus, satu sama lain sebelumnya hanya pernah bertemu lewat Internet.[1][2][3] Pembunuh internet juga adalah sebutan yang d...

Austrian psychoanalyst (1884–1939) This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: We should fix the citation style, per WP:PAREN and [1]. Please help improve this article if you can. (December 2022) (Learn how and when to remove this message) Otto RankBornOtto Rosenfeld22 April 1884 (1884-04-22)Vienna, Austria-HungaryDied31 October 1939(1939-10-31) (aged 55)New York City, USNationalityAustrianKnown forPsychoanalytic look at he...

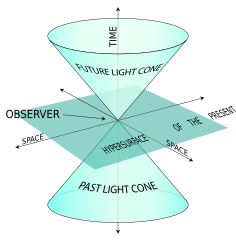
Cosmological model This article's factual accuracy is disputed. Relevant discussion may be found on the talk page. Please help to ensure that disputed statements are reliably sourced. (May 2018) (Learn how and when to remove this message) General relativity G μ ν + Λ g μ ν = κ T μ ν {\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\kappa }T_{\mu \nu }} Introduction HistoryTimelineTests Mathematical formulation Fundamental concepts Equiv...