Witsenhausen's counterexample
|
Read other articles:

Kami Bukan Malaikat 2Genre Drama Komedi Religi PembuatMD EntertainmentDitulis olehHilman HariwijayaSkenarioHilman HariwijayaSutradaraAkbar BhaktiPemeran Oka Antara Donita Niken Anjani Reza Pahlevi Dinda Kanya Dewi Rama Michael Penggubah lagu temaWaliLagu pembukaSholawat — WaliLagu penutupSholawat — WaliNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim2Jmlh. episode30 (daftar episode)ProduksiProduser Dhamoo Punjabi Manoj Punjabi Pengaturan kameraMulti-kameraDurasi60 menitRumah pr...

Arief Budiarto Informasi pribadiLahir13 September 1977 (umur 46)Semarang, Jawa TengahKebangsaanIndonesiaAlma materSMA Taruna Nusantara (1996) Akademi Angkatan Udara (1999)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan UdaraMasa dinas1999 - 2017Pangkat LetkolSatuanKorps Penerbang (Helikopter)Sunting kotak info • L • B Letkol Pnb. (Purn.) Arief Budiarto, (lahir 13 September 1977) adalah purnawirawan perwira menengah TNI Angkatan Udara[1] dan pensiun ...

Kayan SelatanKecamatanPeta lokasi Kecamatan Kayan SelatanNegara IndonesiaProvinsiKalimantan UtaraKabupatenMalinauPemerintahan • CamatElpis Yedija, S.STP[1]Populasi (2022)[2] • Total1.995 jiwa • Kepadatan0,73/km2 (1,9/sq mi)Kode Kemendagri65.02.10 Kode BPS6501020 Luas2.741,50 km²Desa/kelurahan5/- Kayan Selatan adalah sebuah kecamatan di Kabupaten Malinau, Provinsi Kalimantan Utara, Indonesia. Kayan Selatan merupakan pemekaran ...

Je n'ai que mon âme Chanson de Natasha St-Pier auConcours Eurovision de la chanson 2001 Sortie 2001 Langue Français, anglais Genre Pop Auteur-compositeur J. Kapler Chansons représentant la France au Concours Eurovision de la chanson On aura le ciel(2000) Il faut du temps(2002)modifier Je n'ai que mon âme Single de Natasha St-Pierextrait de l'album À chacun son histoire Face B All I Have Is My SoulPrès d'une autre Sortie 30 avril 2001 Enregistré Hauts De Gammes Studio, Boulog...

Foto tahun 1999 yang memperlihatkan sisi timur laut proyek perumahan Cabrini–Green di Chicago, salah satu dari banyak upaya pembaruan perkotaan. Peremajaan kota (Inggris: urban renewal atau urban regeneration), merupakan suatu program pembangunan kembali pada lahan di daerah dengan penggunaan lahan perkotaan yang kepadatannya sedang hingga tinggi. Selama ini pembaruan telah mencatat berbagai keberhasilan maupun kegagalan. Perwujudannya secara modern dimulai pada akhir abad ke-19 di nega...

Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) Artikel ini mungkin mengandung riset asli. Anda dapat membantu memperbaikinya dengan memastikan pernyataan yang dibuat dan menambahkan referensi. Pernyataan yang berpangku pada riset asli harus dihapus. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini mem...

这是西班牙语人名,首姓或父姓是「马杜罗」,次姓或母姓(母親的父姓)是「莫罗斯」。 尼古拉斯·馬杜羅Nicolás Maduro Moros 委内瑞拉总统现任就任日期2013年4月19日代理:2013年3月5日-2013年4月19日2019年-2023年,與胡安·瓜伊多爭位副总统豪尔赫·阿雷亚萨(英语:Jorge Arreaza)(2013-2016年)阿里斯托武洛·伊斯图里斯(英语:Aristóbulo Istúriz)(2016-2017年)塔雷克·埃尔·艾�...

Стратовулкан Майон Тавурвур — активный стратовулкан в Папуа — Новой Гвинее близ города Рабаул на острове Новая Британия Стратовулка́н (от лат. stratum «слой»), или слоистый вулкан — тип вулкана, имеющий коническую форму и сложенный из множества затвердевших с...

Alloy of copper and zinc Arsenical brass redirects here. Not to be confused with arsenical bronze or arsenical copper. For other uses, see Brass (disambiguation). Islamic Golden Age brass astrolabe Brass lectern with an eagle. Attributed to Aert van Tricht, Limburg (Netherlands), c. 1500. Brass is an alloy of copper (Cu) and zinc (Zn), in proportions which can be varied to achieve different colours and mechanical, electrical, acoustic, and chemical properties,[1] but copper typically ...

Aravanis (right), the intersex brides of god Aravan (left), mourn his death. Part of a series onLGBT themes in mythology Regional mythologies In European mythology In Classical mythology In Asian mythology In East Asian mythology In Chinese mythology In West Asian mythologies In South Asian mythology In Hindu mythology In African diasporic mythologies Related fiction genres LGBT themes in fairy tales LGBT themes in comics LGBT themes in mythology LGBT themes in horror fiction LGBT themes in ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Jerome Pearson (kelahiran 1938) adalah insinyur Amerika Serikat dan ilmuwan angkasa yang terkenal untuk karyanya dalam lift luar angkasa dan lift luar angkasa bulan. Ia adalah ketua STAR, Inc., dan telah mengembangkan pesawat dan pesawat luar angkasa ...

British WW1 biplane fighter aircraft 5F.1 Dolphin Dolphin Mk I composite airframe displayed at the Royal Air Force Museum London, 2013 Role FighterType of aircraft Manufacturer Sopwith Aviation Company Designer Herbert Smith (aircraft designer) First flight 23 May 1917 Introduction February 1918 Primary users Royal Flying CorpsRoyal Air Force Number built 2,072[1] The Sopwith 5F.1 Dolphin was a British fighter aircraft manufactured by the Sopwith Aviation Company. It was used by ...

2nd SFFCC Awards December 15, 2003 Best Picture: Lost in Translation The 2nd San Francisco Film Critics Circle Awards, honoring the best in film for 2003, were given on 15 December 2003. Winners Peter Jackson, Best Director winner Bill Murray, Best Actor winner Charlize Theron, Best Actress winner Peter Sarsgaard, Best Supporting Actor winner Patricia Clarkson, Best Supporting Actress winner Best Picture: Lost in Translation Best Director: Peter Jackson - The Lord of the Rings: The Return of...

Historical region of Anatolia Not to be confused with Chaldea. Theme of ChaldiaΧαλδία, θέμα ΧαλδίαςTheme of the Byzantine Empirec. 820/840–1091/10951098–11261140–1204Map of the administrative structure of the Byzantine Empire in 842. Chaldia's strategic location in the north-easternmost corner of the Empire is evident.CapitalTrapezusHistorical eraMiddle Ages• Establishment as a theme c. 820/840• Autonomy from Byzantine rule after Seljuk incursions 1091/109...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2010) (Learn how and when to remove this message) This article's lead section may be too short to adequately summarize the key points. Please consid...

International Synod held in Dordrecht in 1618–1619, by the Dutch Reformed Church Dates in this article are according to the Julian Calendar. Sources using the Old Style calendar will need to be adjusted by adding ten days. The Synod of Dort. The Arminians are seated at the table in the middle.[citation needed] The Synod of Dort (also known as the Synod of Dordt or the Synod of Dordrecht) was a European transnational Synod held in Dordrecht in 1618–1619, by the Dutch Reformed Churc...

Attempting to influence government official Lobbyist redirects here. For the TV series, see Lobbyist (TV series). Lobbying is a form of advocacy, which lawfully attempts to directly influence legislators or government officials, such as regulatory agencies or judiciary.[1] Lobbying involves direct, face-to-face contact and is carried out by various entities, including individuals acting as voters, constituents, or private citizens; corporations pursuing their business interests; non-p...

لمعانٍ أخرى، طالع ريدينغ (توضيح). ريدينغ الإحداثيات 38°31′09″N 95°57′33″W / 38.5192°N 95.9592°W / 38.5192; -95.9592 [1] تاريخ التأسيس 1870 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة ليون خصائص جغرافية المساحة 0.525885 كيلومتر مرب...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: List of Puerto Rico executive offices – news · newspapers · books · scholar · JSTOR (December 2012) (Learn how and when to remove this message) Part of a series on theExecutive branch of thegovernment of Puerto Rico Office of the Governor Chief of Staff Executive offices Governor's Advisory Board Office o...
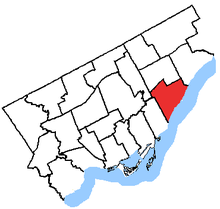
Scarborough-Sud-Ouest Circonscription électorale provinciale du Canada Données clés Création 1996 Localisation Province Ontario Superficie 32 km2 Représentation politique Député Doly Begum (en) Parti politique Néo-démocrate Élu(e) en 2018 Démographie Population 110 280 hab. (2016) Densité 3 446,25 hab./km2 (2016) modifier Scarborough-Sud-Ouest ((en) Scarborough Southwest) est une circonscription provinciale de l'Ontario représentée à l'Assemblée ...











![{\displaystyle k^{2}E[u_{1}^{2}]+E[x_{2}^{2}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df5efd6c8b9c0ee0d39c359b6c6b27f370663fca)






